[通過一題論優化的重要性](原)
忽然發現優化這東西特別的美妙!~~~
先給出一個洛谷OnlineJudge上的題目:
P1903 【模板】分塊/帶修改莫隊(數顏色)
題目描述
墨墨購買了一套N支彩色畫筆(其中有些顏色可能相同),擺成一排,你需要回答墨墨的提問。墨墨會像你發布如下指令:
1、 Q L R代表詢問你從第L支畫筆到第R支畫筆中共有幾種不同顏色的畫筆。
2、 R P Col 把第P支畫筆替換為顏色Col。
為了滿足墨墨的要求,你知道你需要幹什麽了嗎?
輸入輸出格式
輸入格式:
第1行兩個整數N,M,分別代表初始畫筆的數量以及墨墨會做的事情的個數。
第2行N個整數,分別代表初始畫筆排中第i支畫筆的顏色。
第3行到第2+M行,每行分別代表墨墨會做的一件事情,格式見題幹部分。
輸出格式:
對於每一個Query的詢問,你需要在對應的行中給出一個數字,代表第L支畫筆到第R支畫筆中共有幾種不同顏色的畫筆。
輸入輸出樣例
輸入樣例#1:6 5 1 2 3 4 5 5 Q 1 4 Q 2 6 R 1 2 Q 1 4 Q 2 6輸出樣例#1:
4 4 3 4
說明
對於100%的數據,N≤10000,M≤10000,修改操作不多於1000次,所有的輸入數據中出現的所有整數均大於等於1且不超過10^6。
來源:bzoj2120
本題數據為洛谷自造數據,使用CYaRon耗時5分鐘完成數據制作。
這題是莫隊模板題?本蒟蒻開始表示很方......後來看看dalao們都是用到帶修改莫隊,特別是看到了余能dalao......
然而我並不想去學這個東西(太懶了=_=),所以就有了一個依然是離線的想法:
由於題目中已經說了,修改操作不多於1000次,本蒟蒻也就抓住了這個點.我以每次修改將其余的詢問分隔開,然後對於每一段內的詢問,然後很暴力地寫一個莫隊+分塊.
時間復雜度的話,本蒟蒻也不會算了,大概就在10^8~10^9之間徘徊吧...結果TLE40,據說暴力都有50TAT...

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cmath> 5 using namespace std;View Code6 int n,Q,K,blocks; 7 int cnt[10005],ans; 8 struct query{int L,R,tp,index,ans;}a[10005]; 9 struct data{int x,index;}c[10005],cc[10005]; 10 inline int read(){ 11 int x=0; char ch=getchar(); 12 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 13 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 14 return x; 15 } 16 bool cmp_x(data u,data v){return u.x<v.x;} 17 bool cmp_index(data u,data v){return u.index<v.index;} 18 bool cmp_blocks(query u,query v){return u.L/blocks==v.L/blocks?u.R<v.R:u.L<v.L;} 19 bool cmp_id(query u,query v){return u.index<v.index;} 20 void remove(int p){cnt[cc[p].x]--,ans-=cnt[cc[p].x]==0;} 21 void add(int p){cnt[cc[p].x]++,ans+=cnt[cc[p].x]==1;} 22 int main(){ 23 n=read(),Q=read(),blocks=(int)sqrt(n); 24 for (int i=1; i<=n; i++) c[i].x=read(),c[i].index=i; 25 char s[5]; for (int i=1; i<=Q; i++){scanf("%s",s); a[i].tp=s[0]==‘R‘,a[i].L=read(),a[i].R=read(),a[i].index=i;} a[++Q].tp=1; 26 int las=1; 27 for (int K=1; K<=Q; K++) if (a[K].tp){ 28 sort(c+1,c+1+n,cmp_x); 29 int cntnew=1; 30 memset(cc,0,sizeof cc),cc[1].x=1; 31 for (int i=2; i<=n; i++) if (c[i].x==c[i-1].x) cc[i].x=cntnew; else cc[i].x=++cntnew; 32 for (int i=1; i<=n; i++) cc[i].index=c[i].index; 33 sort(c+1,c+1+n,cmp_index); 34 sort(cc+1,cc+1+n,cmp_index); 35 36 sort(a+las,a+1+K-1,cmp_blocks); 37 int curL=1,curR=0; 38 memset(cnt,0,sizeof cnt); ans=0; 39 for (int i=las; i<K; i++){ 40 while (curL<a[i].L) remove(curL++); 41 while (curR>a[i].R) remove(curR--); 42 while (curL>a[i].L) add(--curL); 43 while (curR<a[i].R) add(++curR); 44 a[i].ans=ans; 45 } 46 sort(a+las,a+1+K-1,cmp_id); 47 for (int i=las; i<K; i++) printf("%d\n",a[i].ans); 48 las=K+1,c[a[K].L].x=a[K].R; 49 } 50 return 0; 51 }
然後又表臉地加了O3優化,快了一些,依然TLE40.

1 %:pragma GCC optimize(3) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 int n,Q,K,blocks; 8 int cnt[10005],ans; 9 struct query{int L,R,tp,index,ans;}a[10005]; 10 struct data{int x,index;}c[10005],cc[10005]; 11 inline int read(){ 12 int x=0; char ch=getchar(); 13 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 14 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 15 return x; 16 } 17 bool cmp_x(data u,data v){return u.x<v.x;} 18 bool cmp_index(data u,data v){return u.index<v.index;} 19 bool cmp_blocks(query u,query v){return u.L/blocks==v.L/blocks?u.R<v.R:u.L<v.L;} 20 bool cmp_id(query u,query v){return u.index<v.index;} 21 void remove(int p){cnt[cc[p].x]--,ans-=cnt[cc[p].x]==0;} 22 void add(int p){cnt[cc[p].x]++,ans+=cnt[cc[p].x]==1;} 23 int main(){ 24 n=read(),Q=read(),blocks=(int)sqrt(n); 25 for (int i=1; i<=n; i++) c[i].x=read(),c[i].index=i; 26 char s[5]; for (int i=1; i<=Q; i++){scanf("%s",s); a[i].tp=s[0]==‘R‘,a[i].L=read(),a[i].R=read(),a[i].index=i;} a[++Q].tp=1; 27 int las=1; 28 for (int K=1; K<=Q; K++) if (a[K].tp){ 29 sort(c+1,c+1+n,cmp_x); 30 int cntnew=1; 31 memset(cc,0,sizeof cc),cc[1].x=1; 32 for (int i=2; i<=n; i++) if (c[i].x==c[i-1].x) cc[i].x=cntnew; else cc[i].x=++cntnew; 33 for (int i=1; i<=n; i++) cc[i].index=c[i].index; 34 sort(c+1,c+1+n,cmp_index); 35 sort(cc+1,cc+1+n,cmp_index); 36 37 sort(a+las,a+1+K-1,cmp_blocks); 38 int curL=1,curR=0; 39 memset(cnt,0,sizeof cnt); ans=0; 40 for (int i=las; i<K; i++){ 41 while (curL<a[i].L) remove(curL++); 42 while (curR>a[i].R) remove(curR--); 43 while (curL>a[i].L) add(--curL); 44 while (curR<a[i].R) add(++curR); 45 a[i].ans=ans; 46 } 47 sort(a+las,a+1+K-1,cmp_id); 48 for (int i=las; i<K; i++) printf("%d\n",a[i].ans); 49 las=K+1,c[a[K].L].x=a[K].R; 50 } 51 return 0; 52 }View Code
後來調試時發現,幾個排序的地方(離散這塊,如圖)就占用了5s的時間,去掉3個排序,就只要0.2s了.

但是問題是怎麽去掉排序???
還是慢慢來,一個一個改.先發現了,cc這個排序大可不必,完全可以用一個輔助數組ccc來完成,這樣這部分的復雜度就從O(nlogn)變成了O(n)了.
結果也好歹多了10分,TLE50.此時極端數據需要3s左右才能跑完.

1 %:pragma GCC optimize(3) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 int n,Q,K,blocks; 8 int cnt[10005],ans; 9 struct query{int L,R,tp,index,ans;}a[10005]; 10 struct data{int x,index;}c[10005],cc[10005],ccc[10005]; 11 inline int read(){ 12 int x=0; char ch=getchar(); 13 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 14 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 15 return x; 16 } 17 bool cmp_x(data u,data v){return u.x<v.x;} 18 bool cmp_index(data u,data v){return u.index<v.index;} 19 bool cmp_blocks(query u,query v){return u.L/blocks==v.L/blocks?u.R<v.R:u.L<v.L;} 20 bool cmp_id(query u,query v){return u.index<v.index;} 21 void remove(int p){cnt[cc[p].x]--,ans-=cnt[cc[p].x]==0;} 22 void add(int p){cnt[cc[p].x]++,ans+=cnt[cc[p].x]==1;} 23 int main(){ 24 n=read(),Q=read(),blocks=(int)sqrt(n); 25 for (int i=1; i<=n; i++) c[i].x=read(),c[i].index=i; 26 char s[5]; for (int i=1; i<=Q; i++){scanf("%s",s); a[i].tp=s[0]==‘R‘,a[i].L=read(),a[i].R=read(),a[i].index=i;} a[++Q].tp=1; 27 int las=1; 28 for (int K=1; K<=Q; K++) if (a[K].tp){ 29 sort(c+1,c+1+n,cmp_x); 30 int cntnew=1; 31 memset(cc,0,sizeof cc),cc[1].x=1; 32 for (int i=2; i<=n; i++) if (c[i].x==c[i-1].x) cc[i].x=cntnew; else cc[i].x=++cntnew; 33 for (int i=1; i<=n; i++) cc[i].index=c[i].index; 34 sort(c+1,c+1+n,cmp_index); 35 for (int i=1; i<=n; i++) ccc[cc[i].index].x=cc[i].x; 36 for (int i=1; i<=n; i++) cc[i].x=ccc[i].x,cc[i].index=c[i].index; 37 38 sort(a+las,a+1+K-1,cmp_blocks); 39 int curL=1,curR=0; 40 memset(cnt,0,sizeof cnt); ans=0; 41 for (int i=las; i<K; i++){ 42 while (curL<a[i].L) remove(curL++); 43 while (curR>a[i].R) remove(curR--); 44 while (curL>a[i].L) add(--curL); 45 while (curR<a[i].R) add(++curR); 46 a[i].ans=ans; 47 } 48 sort(a+las,a+1+K-1,cmp_id); 49 for (int i=las; i<K; i++) printf("%d\n",a[i].ans); 50 las=K+1,c[a[K].L].x=a[K].R; 51 } 52 return 0; 53 }View Code
繼續思考,發現圖中的第二個排序也可以省去,因為這一個排序的作用很小,主要是在這裏有用(如圖).
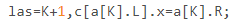
那其實,這裏完全可以O(n)查找一下搞定,反而會省去O(nlogn)的排序.結果就TLE80了,很雞凍.
此時極端數據要1.4s左右能跑完.

1 %:pragma GCC optimize(3) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 int n,Q,K,blocks; 8 int cnt[10005],ans; 9 struct query{int L,R,tp,index,ans;}a[10005]; 10 struct data{int x,index;}c[10005],cc[10005],ccc[10005]; 11 inline int read(){ 12 int x=0; char ch=getchar(); 13 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 14 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 15 return x; 16 } 17 bool cmp_x(data u,data v){return u.x<v.x;} 18 bool cmp_index(data u,data v){return u.index<v.index;} 19 bool cmp_blocks(query u,query v){return u.L/blocks==v.L/blocks?u.R<v.R:u.L<v.L;} 20 bool cmp_id(query u,query v){return u.index<v.index;} 21 void remove(int p){cnt[cc[p].x]--,ans-=cnt[cc[p].x]==0;} 22 void add(int p){cnt[cc[p].x]++,ans+=cnt[cc[p].x]==1;} 23 int main(){ 24 n=read(),Q=read(),blocks=(int)sqrt(n); 25 for (int i=1; i<=n; i++) c[i].x=read(),c[i].index=i; 26 char s[5]; for (int i=1; i<=Q; i++){scanf("%s",s); a[i].tp=s[0]==‘R‘,a[i].L=read(),a[i].R=read(),a[i].index=i;} a[++Q].tp=1; 27 int las=1; 28 for (int K=1; K<=Q; K++) if (a[K].tp){ 29 sort(c+1,c+1+n,cmp_x); 30 int cntnew=1; 31 memset(cc,0,sizeof cc),cc[1].x=1; 32 for (int i=2; i<=n; i++) if (c[i].x==c[i-1].x) cc[i].x=cntnew; else cc[i].x=++cntnew; 33 for (int i=1; i<=n; i++) cc[i].index=c[i].index; 34 for (int i=1; i<=n; i++) ccc[cc[i].index].x=cc[i].x; 35 for (int i=1; i<=n; i++) cc[i].x=ccc[i].x,cc[i].index=c[i].index; 36 37 sort(a+las,a+1+K-1,cmp_blocks); 38 int curL=1,curR=0; 39 memset(cnt,0,sizeof cnt); ans=0; 40 for (int i=las; i<K; i++){ 41 while (curL<a[i].L) remove(curL++); 42 while (curR>a[i].R) remove(curR--); 43 while (curL>a[i].L) add(--curL); 44 while (curR<a[i].R) add(++curR); 45 a[i].ans=ans; 46 } 47 sort(a+las,a+1+K-1,cmp_id); 48 for (int i=las; i<K; i++) printf("%d\n",a[i].ans); 49 las=K+1; 50 for (int i=1; i<=n; i++) if (c[i].index==a[K].L) c[i].x=a[K].R; 51 } 52 return 0; 53 }View Code
接下來就是攻克最頂端的排序.這個排序還是有點用的,因此稍稍要考慮充分一點.
考慮到(下圖)修改只是修改一個值,那麽其他的值的順序還是不變的,只需要調整被修改的位置與其他的位置的順序,因此又一個nlogn被改成了n
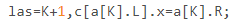
要註意的是,在最開始時,也要先將c數組排成有序的.此時,極端數據只需0.2s了,然後就AC了!~~~

1 %:pragma GCC optimize(3) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 int n,Q,K,blocks; 8 int cnt[10005],ans; 9 struct query{int L,R,tp,index,ans;}a[10005]; 10 struct data{int x,index;}c[10005],cc[10005],ccc[10005]; 11 inline int read(){ 12 int x=0; char ch=getchar(); 13 while (ch<‘0‘||ch>‘9‘) ch=getchar(); 14 while (ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); 15 return x; 16 } 17 bool cmp_x(data u,data v){return u.x<v.x;} 18 bool cmp_index(data u,data v){return u.index<v.index;} 19 bool cmp_blocks(query u,query v){return u.L/blocks==v.L/blocks?u.R<v.R:u.L<v.L;} 20 bool cmp_id(query u,query v){return u.index<v.index;} 21 void remove(int p){cnt[cc[p].x]--,ans-=cnt[cc[p].x]==0;} 22 void add(int p){cnt[cc[p].x]++,ans+=cnt[cc[p].x]==1;} 23 int main(){ 24 n=read(),Q=read(),blocks=(int)sqrt(n); 25 for (int i=1; i<=n; i++) c[i].x=read(),c[i].index=i; sort(c+1,c+1+n,cmp_x); 26 char s[5]; for (int i=1; i<=Q; i++){scanf("%s",s); a[i].tp=s[0]==‘R‘,a[i].L=read(),a[i].R=read(),a[i].index=i;} a[++Q].tp=1; 27 int las=1; 28 for (int K=1; K<=Q; K++) if (a[K].tp){ 29 int cntnew=1; 30 memset(cc,0,sizeof cc),cc[1].x=1; 31 for (int i=2; i<=n; i++) if (c[i].x==c[i-1].x) cc[i].x=cntnew; else cc[i].x=++cntnew; 32 for (int i=1; i<=n; i++) cc[i].index=c[i].index; 33 for (int i=1; i<=n; i++) ccc[cc[i].index].x=cc[i].x; 34 for (int i=1; i<=n; i++) cc[i].x=ccc[i].x,cc[i].index=c[i].index; 35 sort(a+las,a+1+K-1,cmp_blocks); 36 int curL=1,curR=0; 37 memset(cnt,0,sizeof cnt); ans=0; 38 for (int i=las; i<K; i++){ 39 while (curL<a[i].L) remove(curL++); 40 while (curR>a[i].R) remove(curR--); 41 while (curL>a[i].L) add(--curL); 42 while (curR<a[i].R) add(++curR); 43 a[i].ans=ans; 44 } 45 sort(a+las,a+1+K-1,cmp_id); 46 for (int i=las; i<K; i++) printf("%d\n",a[i].ans); 47 las=K+1; int p; 48 for (int i=1; i<=n; i++) if (c[i].index==a[K].L){p=i,c[i].x=a[K].R; break;} 49 while (p<n&&c[p].x>c[p+1].x) swap(c[p],c[p+1]),p++; 50 while (p>1&&c[p].x<c[p-1].x) swap(c[p],c[p-1]),p--; 51 } 52 return 0; 53 }View Code
通過這一題,我們發現,對於某一題,並不是都需要高端算法,有時候在暴力的基礎上(莫隊和分塊也是特殊的暴力)在合適的地方加點優化,會有意想不到的收獲!!!
[通過一題論優化的重要性](原)

