數據 open for 習慣 continue cst cin aps c11

無語凝噎（wordless）

寒蟬淒切，對長亭晚，驟雨初歇。都門帳飲無緒，留戀處，蘭舟催發。執手相看淚眼，竟無語凝噎。念去去，千裏煙波，暮靄沈沈楚天闊。
多情自古傷離別，更那堪，冷落清秋節！今宵酒醒何處？楊柳岸，曉風殘月。此去經年，應是良辰好景虛設。便縱有千種風情，更與何人說！
——宋·柳永《雨霖鈴》
字雖好，只是柳永傷感。執手相看淚眼，竟無語凝噎。太不合此情此景。
——愛新覺羅氏胤禛

西施與範蠡泛舟而去……不對，場景不對，咳咳。在甄嬛前往蓬萊洲之前，她與皇上在碧桐書院告別。為了這可能會長達數月的離別，兩個人都似乎有很多話要對對方說，卻都無語凝噎。這時，皇上突然發話：“嬛嬛啊，既然你我都說不出話來，那這時間也不好打發，我們來數三角形吧。”為了滿足皇上突發而來的童趣，甄嬛欣然陪同了。可這……紙上是一張n*m的格子方陣，即有(n+1)*(m+1)個格點。每個格子都是邊長為1的正方形。而他們要數的，則是任取3個格點作為三角形的頂點所形成的直角三角形且該三角形面積為s/2的個數。甄嬛數的頭都暈了，她現在只想知道滿足條件的三角形個數 mod (10^9+7)

輸入格式：

第一行3個正整數n，m，s, 意義如題

輸出格式：

僅一個整數，為甄嬛與滿足條件的三角形個數 mod (10^9+7)

樣例輸入：

1 1 1

樣例輸出：

4

數據範圍：

對於10%的數據：n<=10
對於另外40%的數據：s為質數
對於100%的數據：1<=n,m,s<=10^8

時間限制：

1S

空間限制：

128M

這題剛開始實在是想的太簡單了,習慣性認為直角邊都在網格上,其實不然,還有不在網格上的情況沒有發現. 先說直角邊在網格上的情況: 由於他是直角三角形,肯定被包含在一個合法矩形內,而每個矩形都包含了4個這種三角形,所以,我們枚舉矩形的長寬a,b,對於每一組a,b,我們可以計算出這種情況中的直角三角形的總數. 總數為max(0,n-a+1)*max(0,m-b+1)*4+max(0,m-a+1)*max(0,n-b+1)*4. 再說直角邊不在網格上的情況: 對於這一類直角三角形,我們總能在它邊上找到兩個相似三角形,如下圖: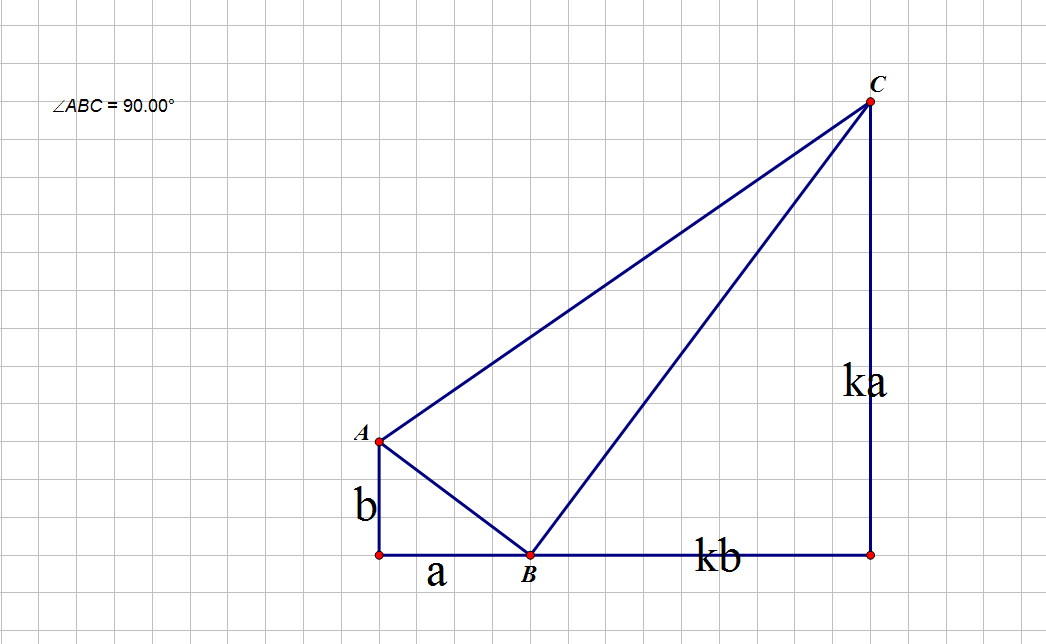

三角形abc邊上總有兩個相似三角形.我們設相似比為k,且k>=1.

在上圖中,我們要知道a,b,k分別是多少,可以通過枚舉的方法實現.

由於:AB*BC/2=S/2,則根號(a*a+b*b)*根號(ka*ka+kb*kb)=S,化簡得k(a*a+b*b)=S.

由於S在1e8範圍內,我們可以枚舉a,b,用根號S*根號S的時間(其實遠遠不到).

由於我們要保證k>=1,所以a*a+b*b<=S.

而比例系數並不一定是整數,整數的應該是a,b,ka,kb,所以不能掉下這個坑啊.

在上圖中,整個三角形的橫向長度為la=a+kb,縱向長度為lb=max(b,ka);

所以這一種情況中,合法三角形數量為max(0,n-la+1)*max(0,m-lb+1).

由於可以旋轉,即橫向長度和縱向長度是相對的,所以可以將la和lb互換.

這種情況中,合法三角形數量為max(0,n-la+1)*max(0,m-lb+1).

又由於可翻轉性和對稱性,同一個形狀的三角形(不考慮橫縱向)在同一個矩形內可以算4次,即

合法三角形數量為max(0,n-la+1)*max(0,m-lb+1)*4+max(0,n-la+1)*max(0,m-lb+1)*4.

但是需要註意的是,當a*a+b*b=s的時候,說明k=1,即兩個相似三角形全等.

此時,我們枚舉的這個直角三角形對於橫縱向其實是同樣的情況(即不存在橫縱向之分,或者說,在橫向統計和縱向統計中都會統計到這一種三角形),所以這種情況

合法三角形數量為(max(0,n-la+1)*max(0,m-lb+1)*4+max(0,n-la+1)*max(0,m-lb+1)*4)/2.

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 #include<iostream>
 5 #include<cmath>
 6 #define LL long long
 7 using namespace std;
 8 const int TT=1000000007;
 9 int n,m,s,cnt,fac[20005];
10 LL ans,c1,c2,la,lb;
11 int main(){
12     cin>>n>>m>>s; cnt=0; ans=0;
13     for (int i=1; i<=sqrt(s); i++) if (s%i==0) fac[++cnt]=i;
14     for (int i=1; i<=cnt; i++){
15         c1=n-fac[i]+1,c2=m-(s/fac[i])+1;
16         if (c1>0&&c2>0) ans=(ans+(LL)c1*c2)%TT;
17         if (fac[i]*fac[i]==s) continue;
18         c1=m-fac[i]+1,c2=n-(s/fac[i])+1;
19         if (c1>0&&c2>0) ans=(ans+(LL)c1*c2)%TT;
20     }
21     ans*=4; ans%=TT;
22     for (LL a=1; a*a<=s; a++)
23         for (LL b=1; a*a+b*b<=s; b++){
24             LL t=a*a+b*b;
25             if ((s*a)%t==0&&(s*b)%t==0){
26                 la=a+(s*b)/t,lb=max((s*a)/t,b);
27                 c1=max(0LL,n-la+1),c2=max(0LL,m-lb+1);
28                 if (t==s) ans+=c1*c2*2; else ans+=c1*c2*4;
29                 c1=max(0LL,m-la+1),c2=max(0LL,n-lb+1);
30                 if (t==s) ans+=c1*c2*2; else ans+=c1*c2*4;
31                 ans%=TT;
32             }
33         }
34     printf("%lld",(ans+TT)%TT);
35     return 0;
36 }

View Code

無語凝噎（wordless）