2007年到來了。經過2006年一年的修煉，數學神童zouyu終於把0到100000000的Fibonacci數列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部給背了下來。
接下來，CodeStar決定要考考他，於是每問他一個數字，他就要把答案說出來，不過有的數字太長了。所以規定超過4位的只要說出前4位就可以了，可是CodeStar自己又記不住。於是他決定編寫一個程序來測驗zouyu說的是否正確。

經過化簡後可得：

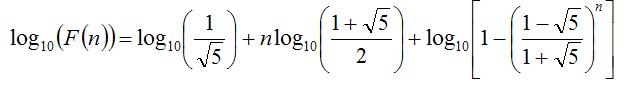
也就是先取以10為底的對數，再取指數，得到整數及前幾位小數部分

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <math.h>
#include <algorithm>

using namespace std;
int a[30];  //<=25
 
int main()
{
    //freopen("1.txt", "r", stdin);
 

    a[1] = 1; a[2] = 1;
    for (int i = 3; i <= 27; i++) {   
        a[i] = a[i-1]+a[i-2];
    }
    int N;
    while (~scanf("%d", &N)) {
        if (N <= 20) {
            printf("%d\n", a[N]);
            continue;
        }
        double t = 0;
        double s = (sqrt(5.0)+1.0)/2.0;
        t = -0.5*log(5.0)/log(10.0) + (double)N*log(s)/log(10.0);
        t = t-floor(t);
        t = pow(10.0, t);
        while (t < 1000)
            t *= 10;
        printf("%d\n", (int)t);
    }


    return 0;
}

[hdu 1568] Fibonacci數列前4位