問題 blog learning 訓練 最大限度 http 監督學習 得到 訓練集

1.監督學習（Supervised Learning）：回歸問題，分類問題 1.1 拿支持向量機舉個例子，分類問題和回歸問題都要根據訓練樣本找到一個實值函數g(x). 回歸問題的要求是：給定一個新的模式，根據訓練集推斷它所對應的輸出y（實數）是多少。也就是使用y=g(x)來推斷任一輸入x所對應的輸出值。 分類問題是：給定一個新的模式，根據訓練集推斷它所對應的類別（如：+1，-1）。也就是使用y=sign(g(x))來推斷任一輸入x所對應的類別。綜上，回歸問題和分類問題的本質一樣，不同僅在於他們的輸出的取值範圍不同。分類問題中，輸出只允許取兩個值；而在回歸問題中，輸出可取任意實數。 1.2支持向量機（SVM） 劃分不同data的分割物 支持向量機，因其英文名為support vector machine，故一般簡稱SVM，通俗來講，它是一種二類分類模型，其基本模型定義為特征空間上的間隔最大的線性分類器，其學習策略便是間隔最大化，最終可轉化為一個凸二次規劃問題的求解。 2.無監督學習 在監督學習中，數據都是被分類的，而在無監督學習中，數據之間沒有區別（沒有正數據和負數據），無監督學習，旨在通過計算機本身將數據進行聚類。 2.1 聚類：將一組無差數據進行同特征歸類。給出算法，給出無差別數據，輸出結果。

---

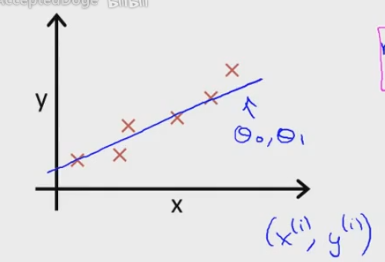
1.回歸（Regression） 回歸算法屬於監督學習，回歸是指自變量X已經給出確定的值或者含義，預測計算出因變量Y的過程。 1.1原料： m:數據集，訓練樣本 x：特征變量 y：目標變量 1.2表示： （x,y）->一個訓練模型 （x(i),y(i)）->具體到i這個訓練模型某一數據點 h->表示假函數（假定的一個函數式）

對於這樣一個 模型，x表示的是房屋面積，y表示的是房屋價格，我們希望通過線性回歸來進行房屋價格預測。 首先假設一個函數hθ（x）=θ0+θ1（x），來表示自變量和因變量的關系， 並且，我們希望函數式hθ（x）能最大限度的代表訓練樣本，也就是說，hθ 函數的值能夠與Y值進行最大的匹配，所以這裏我們運用最小二乘法進行函數匹配，以求出θ0，和θ1的值。

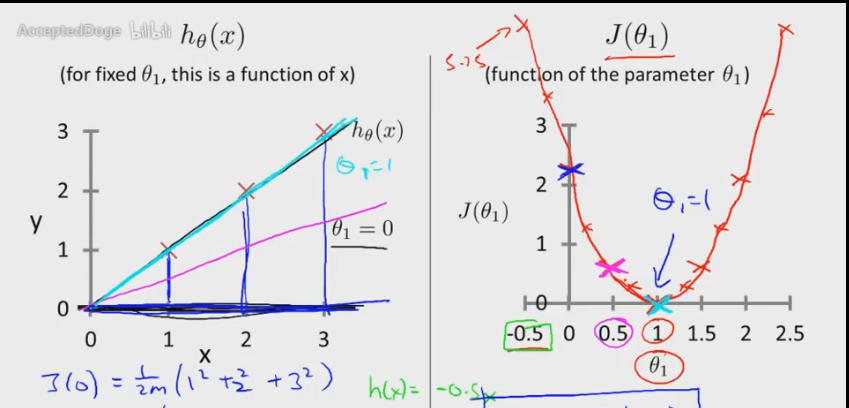
J(θ 0，θ 1)代表對這兩個參數進行求值，J函數又稱為代價函數，m表示的是樣本數量。 在這裏運算時，我們假設θ0為0，可以求出當參數θ1=1時，J函數有最小值，如下圖。

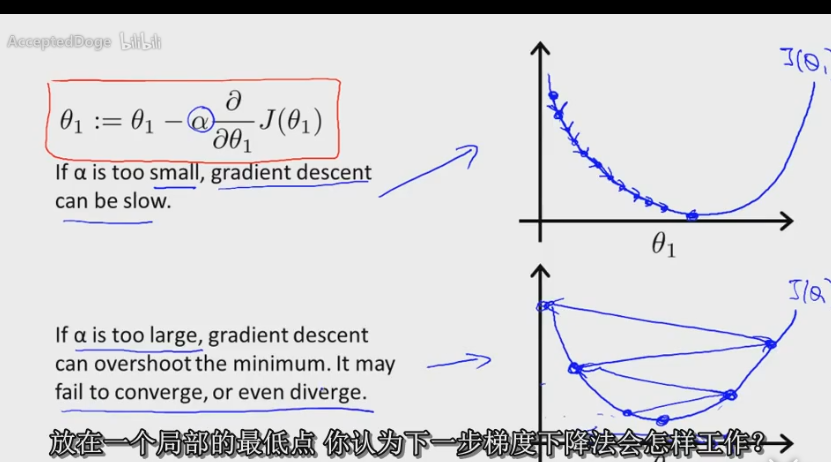
對於上面的J函數，我們不可能要去手工計算參數值，這裏面就要使用梯度下降算法了。 2.梯度下降 梯度下降是尋找最小函數值得過程，相當於你站在山上一步一步的走到山底部的過程 註意：梯度下降時，J(θ0,θ1,θ2.......)中的參數要一同步更新：

ps： :=這個符號是賦值的意思，將右邊賦值給左邊。α是指學習率（下山時的步長），控制以多大幅度更新參數θj 在上方的代碼中，左邊的寫法是正確的，他保證了在計算過程中參數值不會發生變化。而右邊的代碼在第二步時θ0發生了改變，使得J函數發生了改變，梯度下降後的結果也就必然偏離正確結果了。 對於函數式α後面的部分，即αJ(θi)/αθ，他實際上表示的是切線（三維空間中是切面）的斜率，即求偏導，在計算上等同於求微分dj(θi)/dθ(相當於求二維斜率，就是Δy/Δx)，它反映了在最低點的右邊的θ向最低點收斂時的過程是在減少θ的值，而在最低點左邊向最低點收斂時則是在增加θ的值。對於α（學習率）來講，過大的α可能會使得函數錯過最低點，而過小的α可能會使得函數在向最小值收斂時幅度過小，很難快速得到最低值。

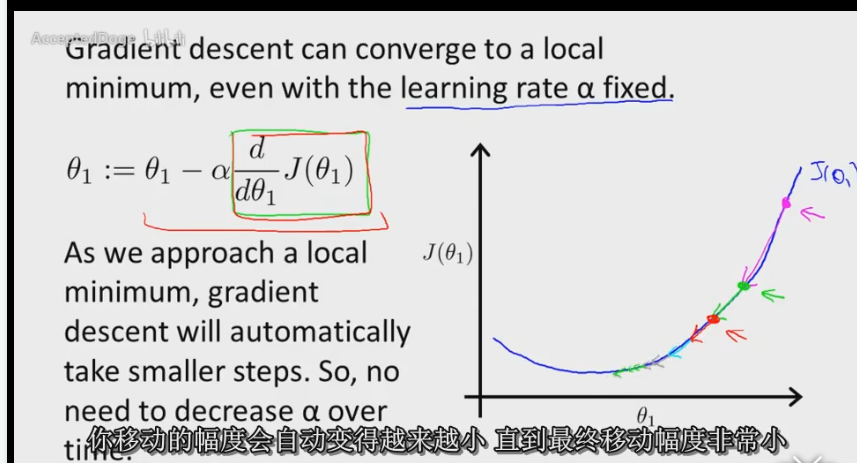
梯度下降算法的一個特點就是在越來越接近最低點時函數的改變幅度會越來越小（斜率越來越小直到0），而在最低點時，函數的值不會在發生變化，因為最低點斜率為0（dj(θi)/dθ=0）

機器學習的一些基礎理論