另一方面，如果 M 滿足(1)式,那麽M必然在以PQ為直徑的圓上.事實上當M為P或者Q時，這是顯然的。當M異於P,Q時，由$\frac{|MB|}{|MC|}=\frac{|PB|}{|PC|}=\lambda,\frac{|MB|}{|MC|}=\frac{|QB|}{|QC|}=\lambda$知MP,MQ分別是$\angle{BMC}$的內角平分線和外交平分線，故$\angle{PMQ}=90^0$,即M在以PQ為直徑的圓上。

評:阿式圓因為涉及到內角平分線和外角平分線又稱為內外圓，在有些高考題中非常的管用.這個圓的定義大家可以和高中教材中橢圓雙曲線的定義做比較，自然會想到以下問題:到兩個定點的乘積為定值的點的軌跡是什麽？

註:卡西尼卵形線圖像：

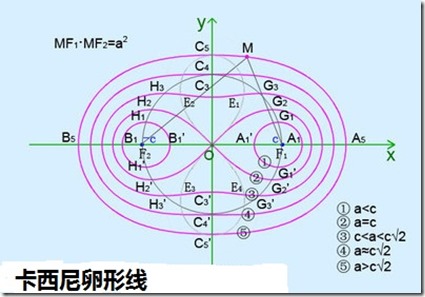
例：

解答:

MT【32】內外圓(Apollonius Circle）的幾何證明