多元高斯(正態)分布

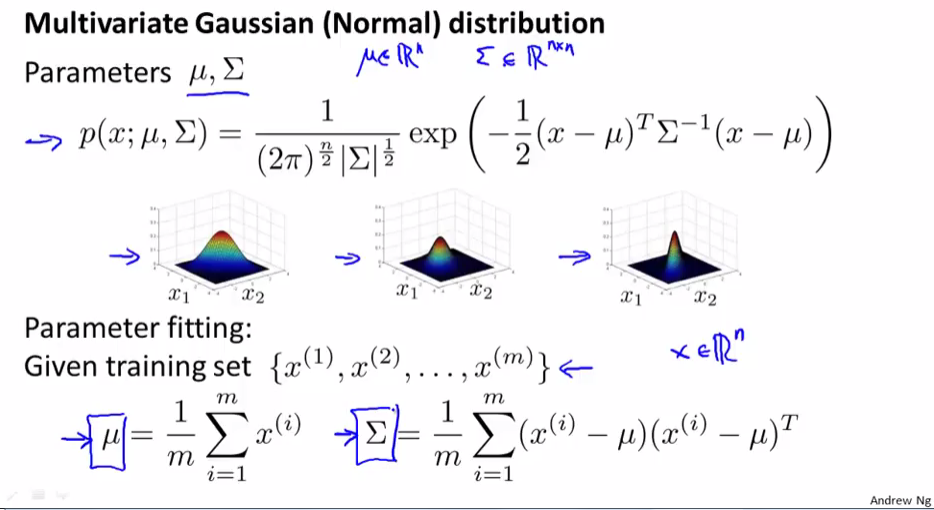
多元高斯分布有兩個參數u和Σ,u是一個n維向量，Σ協方差矩陣是一個n*n維矩陣。改變u與Σ的值可以得到不同的高斯分布。

參數估計（參數擬合），估計u和Σ的公式如上圖所示，u為平均值，Σ為協方差矩陣

使用多元高斯分布來進行異常檢測

首先用我我們的訓練集來擬合參數u和Σ，從而擬合模型p(x)

拿到一個新的樣本，使用p(x)的計算公式計算出p(x)的值，如果p(x)<ε就將它標記為一個異常點

當我們對上圖中那個綠色的點進行異常檢測時，這些紅色的點服從多元高斯正態分布(x1與x2正相關)，算法會將綠色的判斷為異常點，因為它遠離這個高斯分布中心點。

多元高斯分布模型與原來的模型之間的關系（原來的模型是多元高斯分布的一個特例）

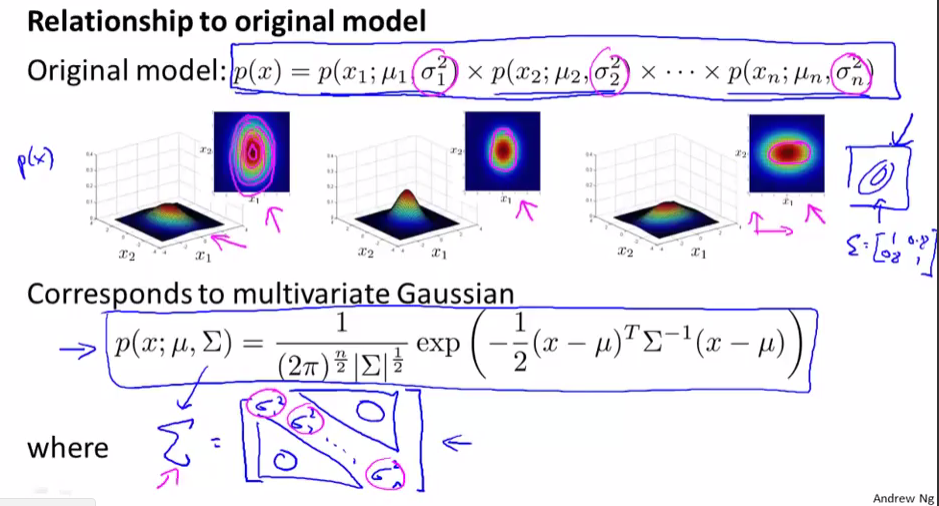
原來的模型p(x)=p(x1)*p(x2)*p(x3).....*p(xn)這個模型那就什麽樣的多元高斯分布呢？

上面圖中三個多元高斯分布的圖型，它們的等高線位於x1或者x2軸向線平行，原來的模型即那就於這樣的高斯分布，即沒有x1,x2的關系約束，即Σ在非對角線上的值為0，只在對角線上有值。

所以原來的模型p(x)對應於下面的多元高斯分布，這個多元高斯分布有個約束條件，即Σ只在對角線上有值(分別為σ_1²,σ₂².....σ_n²)，在非對角線上的值都為0,不能給不同特征之間的相關性建模。

該用哪個模型？

original model可能使用得更頻繁，多元高斯模型沒有那麽常用，但是它能捕捉到不同特征之間的相關性（正相關或者負相關）

在original model裏面，如果你想捕獲不同特征組合之間的異常（如捕獲CPU load與memory use之間組合的不正常情況），我們需要建立一個新的feature=這兩個特征之間的組合，如x3=CPU load/memory use.這樣雖然當x1是正常的，x2是正常的，但是如果x1/x2不正常，我們就可以捕獲到這種異常情況。而多元高斯模型可以自動地捕獲不同特征變量之間的相關性。

original model計算比較快，運算量更小，適用於特征量非常多的情況，即n值很大的情況；而當n很大時，多元高斯模型要計算Σ的逆矩陣（為n*n），這個計算量非常大，所以多元高斯模型不適合於n值很大的情況

對於original model即使m很小，即訓練集很小，也可以運行的也可以的；而對於多元高斯模型，在數學上必須滿足m>n,不然Σ就是不可逆的，但是在實際中，我們使用時只有m遠大於n時，即m>=10n（合理的經驗法則）時才使用多元高斯模型。因為Σ是一個n*n的矩陣，有n*n/2個參數（Σ為對稱矩陣）需要計算，如果我們的訓練樣本不夠大的話，就不能很好的評估這些參數。

實際中，original model更常用，如果我們想捕捉變量之間的相關性的話就另外創建一個新的feature來捕捉特定的不正常值的組合。

在訓練集很大，n不大的情況下，多元高斯模型可以考慮，可以幫你省去創建新的feature的時間。

當擬合多元高斯模型時，如果發現Σ不可逆時（奇異的），會有兩種情況導致，一種情況是它沒有滿足m>n的條件，第二種情況是有冗余的特征變量（如x1=x2,x3=x4+x5(x3是冗余的，沒有提供額外的信息)），即線性相關的特征變量。所以當在實際中遇到Σ不可逆時，檢查m是否比n大得多，然後檢查是否有冗余的特征變量（如刪掉x1,x3），這樣就能很好地運行了，但是我們遇到這些問題的可能性會比較低，我們可以直接應用多元高斯模型，不需要擔心Σ不可逆的問題。

總結

1>使用多元高斯模型可以使我們的算法自動捕獲不同特征變量之間的相關性（正相關或者負相關），在組合不正常時將其標識為異常。

異常檢測: 應用多元高斯分布進行異常檢測