baidu 器） ridge 連續概率 重要 eal 函數 應用 map

最小二乘法可以從Cost/Loss function角度去想，這是統計（機器）學習裏面一個重要概念，一般建立模型就是讓loss function最小，而最小二乘法可以認為是 loss function = （y_hat -y )^2的一個特例，類似的像各位說的還可以用各種距離度量來作為loss function而不僅僅是歐氏距離。所以loss function可以說是一種更一般化的說法。

最大似然估計是從概率角度來想這個問題，直觀理解，似然函數在給定參數的條件下就是觀測到一組數據realization的概率（或者概率密度）。最大似然函數的思想就是什麽樣的參數才能使我們觀測到目前這組數據的概率是最大的。

類似的從概率角度想的估計量還有矩估計（moment estimation）。就是通過一階矩 二階矩等列方程，來反解出參數。

有人提到了正態分布。最大似然估計和最小二乘法還有一大區別就是，最大似然估計是需要有分布假設的，屬於參數統計，如果連分布函數都不知道，又怎麽能列出似然函數呢？ 而最小二乘法則沒有這個假設。 二者的相同之處是都把估計問題變成了最優化問題。但是最小二乘法是一個凸優化問題，最大似然估計不一定是。

註：
從優化的角度上來講，負的log likelihood 就是求MLE（最大似然估計）要優化的目標函數。
那麽為啥MLE需要設置分布這麽麻煩，還有這麽多應用，因為當likelihood設置正確的時候，這個目標函數給出的解最efficient。

那麽為啥有這麽多人把MLE和LOSE搞混，因為當likelihood用的是gaussian的時候，由於gaussian kernel裏有個類似於Euclidean distance的東西，一求log就變成square loss了，導致解和OLSE是一樣的。而碰巧剛接觸MLE的時候基本都是gaussian假設，這才導致很多人分不清楚。

從概率論的角度：
Least Square 的解析解可以用 Gaussian 分布以及最大似然估計求得
Ridge 回歸可以用 Gaussian 分布和最大後驗估計解釋
LASSO 回歸可以用 Laplace 分布和最大後驗估計解釋

-------------------------------------------------------------------

下面是上述三種的推導
註意：
首先知道什麽是：高斯分布、拉普拉斯分布、最大似然估計，最大後驗估計（MAP）。
按照李航博士的觀點，機器學習三要素為：模型、策略、算法。
一種模型可以有多種求解策略，每一種求解策略可能最終又有多種計算方法。
以下只推導模型策略，不講算法。

區別：

最大似然估計不考慮先驗後驗的問題，純粹是選擇一個參數能最大化模型似然度
最大後驗概率是貝葉斯方法，引入參數的先驗概率，結合似然度選擇最佳參數或模型

拉普拉斯分布

• 在概率論與統計學中，拉普拉斯分布是以皮埃爾-西蒙·拉普拉斯的名字命名的一種連續概率分布.由於它可以看作是兩個不同位置的指數分布背靠背拼接在一起，所以它也叫作雙指數分布.兩個相互獨立同概率分布指數隨機變量之間的差別是按照指數分布的隨機時間布朗運動，所以它遵循拉普拉斯分布.
  如果隨機變量的概率密度函數為
  

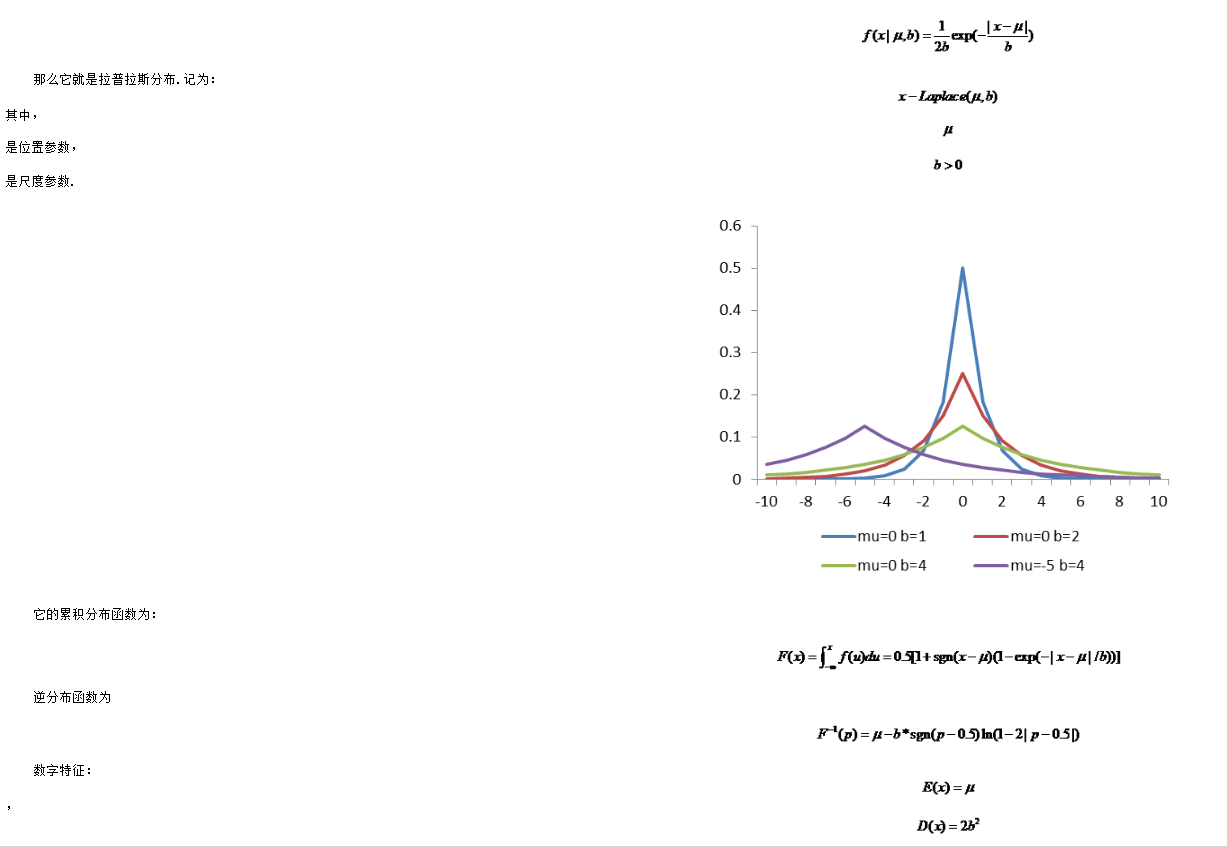
極大既然估計和高斯分布推導最小二乘、LASSO、Ridge回歸