題目：洛谷P1514、Vijos P1777、codevs1066。

題目大意：有一個$n×m$的矩陣，每個點都有一個高度，可以在第一行的任意點建立蓄水廠。現在要把水輸到最後一行的所有點上，規定水只能流到高度比當前點小的點上。先讓你判斷能否輸到所有點上，如能，輸出最少建多少個蓄水廠；如不能，輸出最多能輸到幾個點上。

解題思路：首先把第一行所有點塞進隊列裏，跑BFS，找出所有能到的點，然後判斷能否輸到最後一行所有點上。如果不能，輸出最後一行能被輸到的點的總數。如果能的話，我們依次把第一行每個點能輸到的點求出來。

下面證明在能輸到最後一行所有點的情況下，第一行每個點能輸到最後一行的點一定構成一個連續的區間。

如果出現一個蓄水廠分流到兩個不同的區間，那麽有下圖：

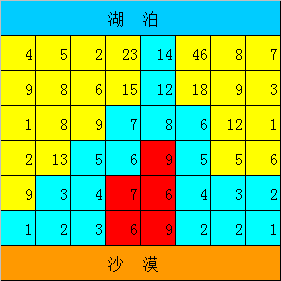
可以發現，紅色區域由於已經被藍色區域包圍，所以無論如何都是無法流到的，說明如果有可行的方案，流到的一定是一個連續的區間。

然後就是區間覆蓋問題，貪心一下就好了。

C++ Code：

#include<cstdio>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,h[505][505],ans;
bool b[505][505];
queue<pair<int,int> >q;
const int dx[]={0,0,1,-1};
const int dy[]={-1,1,0,0};
struct QJ{
	int L,R;
	bool operator<(const QJ& rhs)const{
		if(L!=rhs.L)return L<rhs.L;
		return R>rhs.R;
	}
}a[505];
void bfs(){
	memset(b,1,sizeof b);
	for(int i=1;i<=m;++i){
		b[1][i]=false;
		q.push(make_pair(1,i));
	}
	while(!q.empty()){
		int x=q.front().first,y=q.front().second;
		q.pop();
		for(int i=0;i<4;++i){
			int lx=x+dx[i],ly=y+dy[i];
			if(ly>0&&ly<=m&&lx<=n&&b[lx][ly]&&h[x][y]>h[lx][ly]){
				b[lx][ly]=false;
				q.push(make_pair(lx,ly));
			}
		}
	}
}
void bfs2(int t){
	memset(b,1,sizeof b);
	b[1][t]=false;
	q.push(make_pair(1,t));
	int Lft=20000,Rgt=0;
	while(!q.empty()){
		int x=q.front().first,y=q.front().second;
		q.pop();
		if(x==n){
			if(y<Lft)Lft=y;
			if(y>Rgt)Rgt=y;
		}
		for(int i=0;i<4;++i){
			int lx=x+dx[i],ly=y+dy[i];
			if(ly>0&&ly<=m&&lx<=n&&b[lx][ly]&&h[x][y]>h[lx][ly]){
				b[lx][ly]=false;
				q.push(make_pair(lx,ly));
			}
		}
	}
	a[t].L=Lft;
	a[t].R=Rgt;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
	for(int j=1;j<=m;++j)scanf("%d",&h[i][j]);
	bfs();
	ans=0;
	for(int i=1;i<=m;++i)
	if(b[n][i])++ans;
	if(ans){
		printf("0\n%d\n",ans);
		return 0;
	}
	for(int i=1;i<=m;++i)
	bfs2(i);
	sort(a+1,a+m+1);
	int l=a[1].L,r=a[1].R;
	ans=1;
	while(r<m){
		int p,mx=0;
		for(int i=1;i<=m;++i){
			if(a[i].L<=l)continue;
			if(a[i].L>r+1)break;
			if(mx<a[i].R)mx=a[i].R,p=i;
		}
		l=a[p].L,r=a[p].R;++ans;
	}
	printf("1\n%d\n",ans);
	return 0;
}

[NOIP2010提高組]引水入城