HDU 6206 Apple ( 高精度 && 計算幾何 && 三點構圓求圓心半徑 )
題意 : 給出四個點,問你第四個點是否在前三個點構成的圓內,若在圓外輸出"Accepted",否則輸出"Rejected",題目保證前三個點不在一條直線上。
分析 : 簡單的計算幾何問題,如果能夠知道圓心和半徑(Radius)以及第四個點和圓心的距離(Distance),我們就能夠判斷第四個點是否在圓外,例如Distance > Radius則在圓外。三點構圓 的圓心和半徑是能夠推導出公式的
(參考==> http://blog.csdn.net/death10001/article/details/77389128 )
設 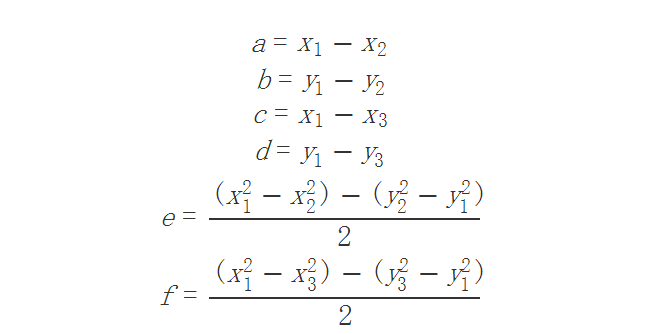 則有
則有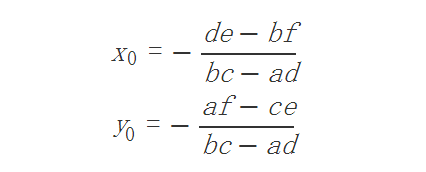
根據兩點間距離公式 R2 = (X - X0)2 + (Y - Y0
[ 2*X*(bc-ad)+(de-bf) / 2(bc-ad) ]2 + [ 2*Y*(bc-ad)+(af-ce) / 2(bc-ad) ]2
發現分母都是一樣,可以通分。然後呢,還是根據兩點間距我們可以用同樣的方法得到第四個點和圓心之間的距離並且分母同樣是2(bc-ad),所以運算的過程當中是不用進行除法操作的,只要比較兩個分子即可,高精度問題也只用BigInteger解決即可。

import java.util.Scanner; import java.util.*; import java.math.*;View Codeimport java.io.*; class PO{ BigInteger x, y; } public class Main{ public static boolean Solve(PO p1, PO p2, PO p3, PO p){ //------------------------------------------------------------------------------------- BigInteger a = p1.x.subtract(p2.x); BigInteger b = p1.y.subtract(p2.y); BigInteger c= p1.x.subtract(p3.x); BigInteger d = p1.y.subtract(p3.y); BigInteger e = (((p1.x).multiply(p1.x)).subtract((p2.x).multiply(p2.x))).subtract(((p2.y).multiply(p2.y)).subtract(((p1.y).multiply(p1.y)))); BigInteger f = (((p1.x).multiply(p1.x)).subtract((p3.x).multiply(p3.x))).subtract(((p3.y).multiply(p3.y)).subtract(((p1.y).multiply(p1.y)))); BigInteger two = new BigInteger("2"); //------------------------------------------------------------------------------------- BigInteger tmp1 = (((p1.x).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((d.multiply(e)).subtract((b.multiply(f)))); tmp1 = tmp1.multiply(tmp1); BigInteger tmp2 = (((p1.y).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((a.multiply(f)).subtract((c.multiply(e)))); tmp2 = tmp2.multiply(tmp2); BigInteger R = tmp1.add(tmp2);///計算出半徑的"長度" ( 實際是代數式的分子 ) //------------------------------------------------------------------------------------- tmp1 = (((p.x).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((d.multiply(e)).subtract((b.multiply(f)))); tmp1 = tmp1.multiply(tmp1); tmp2 = (((p.y).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((a.multiply(f)).subtract((c.multiply(e)))); tmp2 = tmp2.multiply(tmp2); BigInteger Dis = tmp1.add(tmp2);///計算出圓心到第四個點的"距離" if(R.compareTo(Dis) < 0) return true; else return false; } public static void main (String[] args) throws Exception{ Scanner cin = new Scanner(new BufferedInputStream(System.in)); int nCase = cin.nextInt(); for(int t=1; t<=nCase; t++){ PO p1 = new PO(); PO p2 = new PO(); PO p3 = new PO(); PO aim= new PO(); p1.x = cin.nextBigInteger(); p1.y = cin.nextBigInteger(); p2.x = cin.nextBigInteger(); p2.y = cin.nextBigInteger(); p3.x = cin.nextBigInteger(); p3.y = cin.nextBigInteger(); aim.x = cin.nextBigInteger(); aim.y = cin.nextBigInteger(); boolean res = Solve(p1, p2, p3, aim); if(res) System.out.println("Accepted"); else System.out.println("Rejected"); } } }
瞎 : 實際上還有更簡便的方法,直接能用更直接的公式算出圓心 (x0, y0) 和半徑的平方 r^2
x0=((y2-y1)*(y3*y3-y1*y1+x3*x3-x1*x1)-(y3-y1)*(y2*y2-y1*y1+x2*x2-x1*x1))/(2.0*((x3-x1)*(y2-y1)-(x2-x1)*(y3-y1)));
y0=((x2-x1)*(x3*x3-x1*x1+y3*y3-y1*y1)-(x3-x1)*(x2*x2-x1*x1+y2*y2-y1*y1))/(2.0*((y3-y1)*(x2-x1)-(y2-y1)*(x3-x1)));
r^2=(x1-x0)*(x1-x0)+(y1-y0)*(y1-y0);
裏面涉及除法,那就用BigDecimal就能解決了,參考 ==> http://blog.csdn.net/cillyb/article/details/78012069
HDU 6206 Apple ( 高精度 && 計算幾何 && 三點構圓求圓心半徑 )

