卡爾曼濾波的一個簡單demo: 恒定加速度模型
阿新 • • 發佈:2017-09-24
obi vtt efk rtp end atp cee cdn bs4
恒定加速度Kalman模型
1.
scenario:我們想用卡爾曼濾波來追蹤 3D空間中某個具有恒定加速度的物體,我們有一個位置傳感器可以用來觀測物體位置,我們想得到物體的3D位置以及速度。
2. Description :
假設物體狀態由六維vector定義如下:
系統的預測方程為:
假設我們沒有控制輸入,那麽預測方程可以表示如下:
y = Hx
因為我們有位置傳感器,不管是視覺,激光還是雷達,我們可以得到物體在3D空間中的位置,即(x,y,z),那麽系統的觀測方程可以用如下表示:
接下來我們定義初始狀態的協方差矩陣為9x9的單位矩:
接下來定義系統的狀態轉移矩陣 A,若定義狀態間的time
step為 dt
= 1,則此時的A矩陣為:
定義系統的初始觀測協方差矩陣為3x3的對角陣:
:系統的加速度擾動 ,那麽Q可以用如下表示:
3. Implementation :
這裏省略了一些細節,具體代碼請查看我的github主頁:https://github.com/Doodleshr
P = 100.0*np.eye(9) #define dt = 0.05 rather than dt = 1 dt = 0.05
#define H and A according to what we have discused
......
####define observation noise covariance R = 100*np.eye(3) #define process noise matrix Q #from the blog we mentioned how to compute Q from G G = ... a = 0.1 Q = G*G.T*a**2
#system initialization px=0.0 py=0.0 pz=0.0 vx=1 vy=2 vz=3 Xr=[] Yr=[] Zr=[] # #generate position: for i in range(100): # we assume constant acceleratoin for this demo accx = 3 vx += accx * dt px += vx * dt accy = 1 vy += accy * dt py += vy * dt accz = 1 vz += accz * dt pz += vz * dt Xr.append(px) Yr.append(py) Zr.append(pz) # position noise sp = 0.5 Xm = Xr + sp * (np.random.randn(100)) Ym = Yr + sp * (np.random.randn(100)) Zm = Zr + sp * (np.random.randn(100)) #stack measurements measurements = np.vstack((Xm,Ym,Zm)) #define initial state X = np.matrix([0.0, 0.0, 0.0, 1.0, 2.0, 3.0, 3.0, 1.0, 1.0]).T I = np.eye(9) Xx = [] Xy = [] Xz = [] for each_step in range(100): #prediction step: X = A*X #state covariance propogation P = A*P*A.T + Q #measurement covariance propogation S = H*P*H.T + R #Kalman Gain update K = (P*H.T) * np.linalg.pinv(S) # print(K) Z = measurements[:,each_step].reshape(3,1) #corrected/updated x X = X + K*(Z-(H*X)) #update state covariance P: P = (I - (K * H)) * P #store corrected/updated x Xx.append(float(X[0])) Xy.append(float(X[1])) Xz.append(float(X[2]))
4. Result:
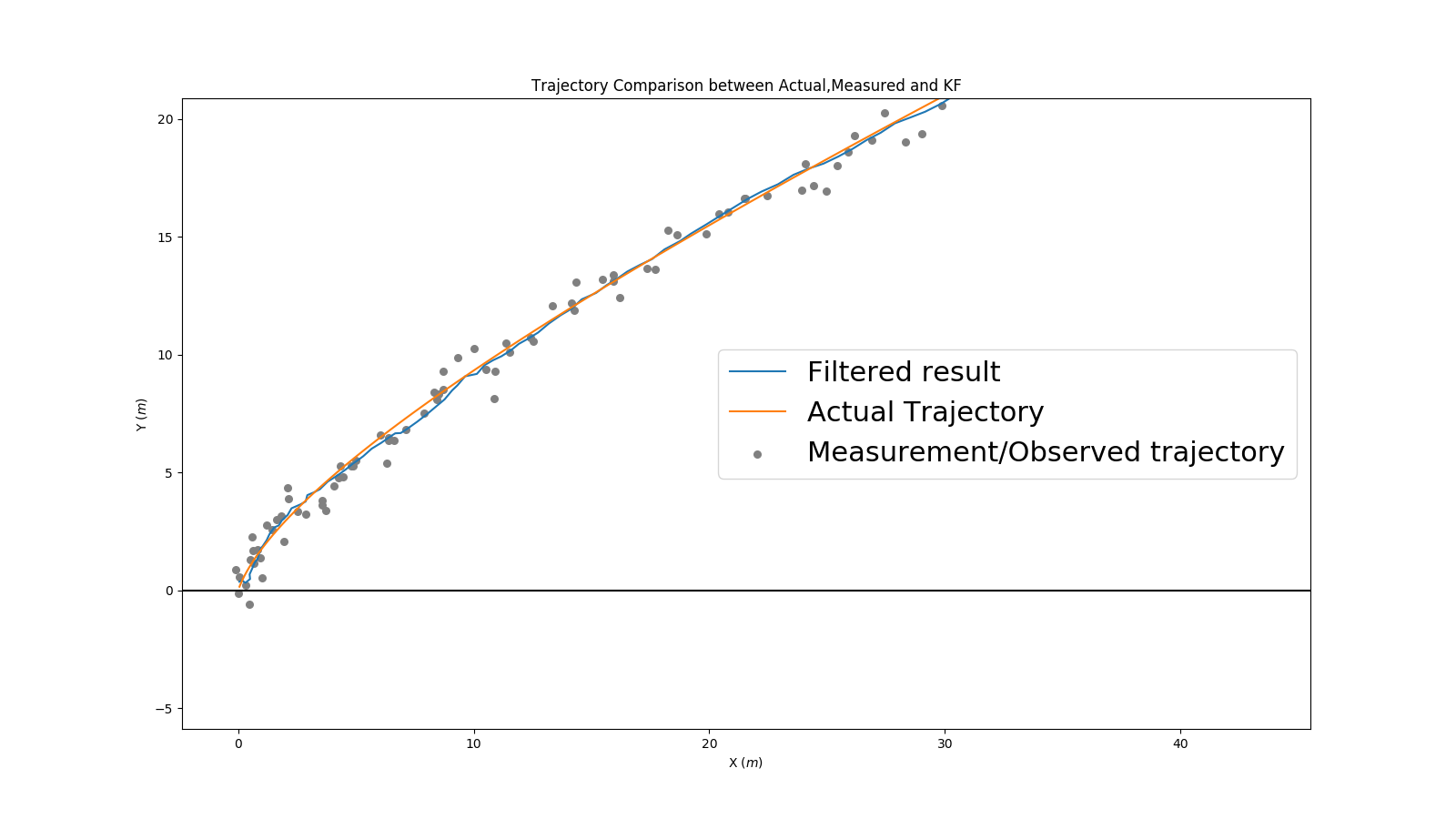
我們可以看到觀測值是很noisy的,但是使用卡爾曼濾波後,軌跡變得平滑許多,也更加貼合實際軌跡,可見卡爾曼濾波是是有效的。
卡爾曼濾波的一個簡單demo: 恒定加速度模型
