卡爾曼濾波
阿新 • • 發佈:2017-09-30
nbsp 應用 一周 log -1 現在 richtext http 一是
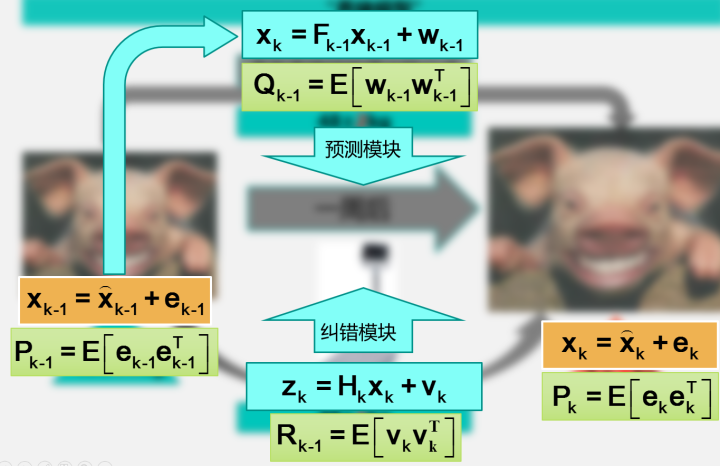
上圖中右邊表示k時刻的狀態值,這個值可以通過預測模塊(也就是根據經驗公式估計豬的體重)和糾錯模塊(也就是直接去稱量豬的體重值)來估計。同樣,預測模塊和糾錯模塊都有著對應的誤差和誤差協方差矩陣。卡爾曼濾波要做的,就是根據貝葉斯估計的相關理論,同時考慮預測模塊和糾錯模塊的協方差,對誤差小的項賦予較大的權重,對誤差大的項賦予較小的權重,並使預測的誤差最小。
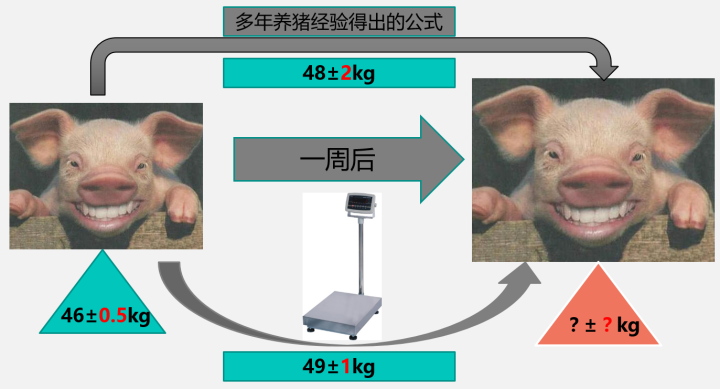
假設我養了一只豬:

一周前,這只豬的體重是46±0.5kg。註意,在這裏我用了±0.5,表示其實我對這只豬一周前的體重並不是那麽確定的,也就是說,46kg這個體重有0.5kg的誤差。
現在,我又養了這只豬一個星期。那麽我想要知道它一個星期之後多重,又大概有多少的誤差?
為了得到一周後的體重,我有兩種方法:一是根據我多年的養豬經驗得到的豬體重公式推求出一個大概的值,另一個就是直接去稱它的體重。當然,兩種方法都有一定的誤差。假設經驗公式得到的體重是48kg,誤差2kg;直接稱體重得到的是49kg,誤差1kg:

上圖的左邊,上一周的豬的體重,可以抽象為也k-1時刻的狀態值,用k-1時刻的最優估計值加上一個誤差項來表示,右邊同理。其中,

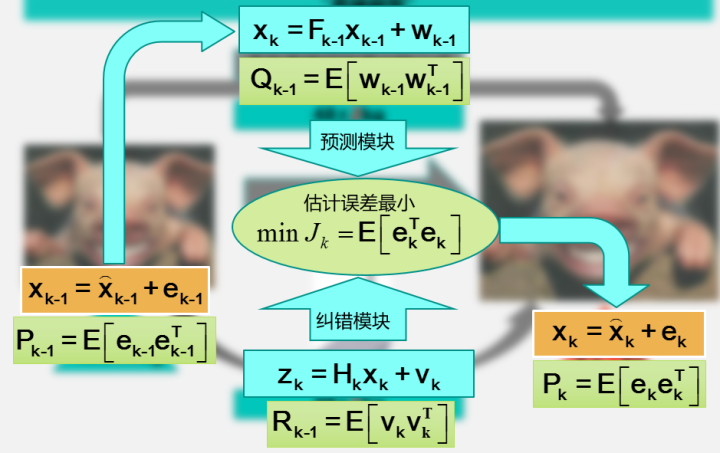
上圖中右邊表示k時刻的狀態值,這個值可以通過預測模塊(也就是根據經驗公式估計豬的體重)和糾錯模塊(也就是直接去稱量豬的體重值)來估計。同樣,預測模塊和糾錯模塊都有著對應的誤差和誤差協方差矩陣。卡爾曼濾波要做的,就是根據貝葉斯估計的相關理論,同時考慮預測模塊和糾錯模塊的協方差,對誤差小的項賦予較大的權重,對誤差大的項賦予較小的權重,並使預測的誤差最小。

具體的實現過程如下:
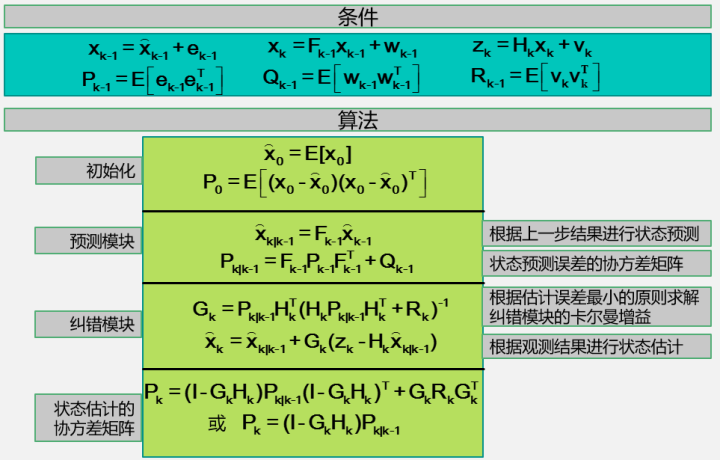
至於具體的這個過程是怎麽推求的,每個參數的詳細解釋又是怎麽樣的,這個在所有介紹卡爾曼的濾波的書上都有講述,也並不是一個帖子就能說清楚的,這裏就不展開講了~
謝謝各位看官~
卡爾曼濾波
