先摘錄書中一段關於樹的定義：

樹(Tree)是n(n>=0)個結點的有限集。n=0時稱為空樹。在任意一棵非空樹中：（1）有且僅有一個特定的稱為根（Root）的結點；（2）當n>1時，其余結點可以分為互不相交的有限集T1、T2、……Tm，其中每一個集合本身又是一棵樹，並且稱為根的子樹（SubTree）。

其實，我個人覺得這段定義還是蠻抽象的。不過，根據定義來看，樹的定義有點像家族的族譜，最上面的是祖父母，然後接著是你的父母親，再往下一層是你和你老婆（或者是老公），然後下一層是你們的兒女，就這樣一層層往下。那麽用一句話來說就是，樹就是不包含回路的無向連通圖。不包含回路，換言之，就是任意兩個結點間有且只有一條路徑。所以，總的來說，如果符合一棵樹，則，一，任意兩個結點之間有且只有一條路徑。二，如果一棵樹有n個結點，則這棵樹有(n-1)條邊。三，在一棵樹中加一條邊，則會構成回路。

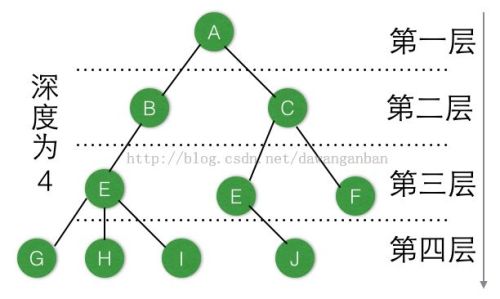
樹也是由一個個結點構成，也就是說，同一棵樹可以有不同的形態，為了確定樹的形態，我們可指定一個特殊的結點，將其稱之為“根節點”。需要註意的是，一棵樹有且只有一個根節點。因為，根節點又是一棵樹起始的地方，所以，根節點又稱為“祖先”。既然，有祖先，就會有父親，兒子。如上圖所示，A就是根節點，B和C就是A的兒子，所以，B和C就稱之為，子節點，但是B又是E的父親，所以，B既是子節點又是父節點。對於像G、H、I、J、F這樣的沒有後代的結點稱為，葉節點（葉節點也稱為終端結點）。如果一個結點既不是葉節點也不是根節點，那麽它就稱之為，內部結點（也稱為分支結點）。

關於樹還有一個概念，就是，深度。什麽是深度呢？深度就是從根節點到該結點層數。比如，G、H、I、J結點的深度就是4,；E、F的深度就是3；B、C的深度就是2。那麽一棵樹的深度就是，結點的最大深度，所以該樹的最大深度就是4。

度。什麽是度？結點擁有的子樹數稱為度。比如B結點的子樹數為1，因為它只有E這麽一棵子樹，所以B結點的度為1；E結點的子樹數為3，因為它的子樹有，G、H、I三棵，所以E結點的度為3。而樹的度，則是樹內各結點的度的最大值。所以，如上圖所示，該圖中的樹的度為3。

森林。對於樹中的每個結點而言，其子樹的集合就是森林。

本文出自 “梵高說我腦子有病” 博客，請務必保留此出處http://chen0547.blog.51cto.com/12489941/1968615

樹的基本定義