小魚幹

【問題描述】

小喵喵有n個小魚幹排成一列，其中第i個小魚幹有兩種屬性，美味度ai和特殊度bi。

現在小喵喵要吃掉一些小魚幹，出於一些原因，小喵喵會吃掉連續的一段區間中的所有小魚幹。

如果吃掉了[l,r]一段區間，那麽小喵喵會獲得一些滿意度。

形式化地，總滿意度=。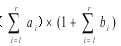

由於只有小喵喵最喜歡的小魚幹的特殊度等於1，所以bi=1的小魚幹數量不會超過400個，其他的bi=0。

現在小喵喵可以選擇任意一段區間，但是有一些小魚幹的美味度是負數，吃掉所有小魚幹不一定會獲得最多的滿意度。所以小喵喵想知道最大能獲得的總滿意度是多少。

【輸入】

第一行一個整數n，表示小魚幹的數量。

第二行n個整數，第i個數為ai，表示美味度。

第三行n個整數，第i個數為bi，表示特殊度。

【輸出】

一行一個整數，表示最大的總滿意度。

【輸入輸出樣例】

【樣例解釋】

吃掉前三個小魚幹會獲得最多的滿意度。其中8=(4+(-2)+2)*(1+0+0+1)

【數據範圍】

對於100%的數據：n≤100000,-10^9≤ai≤10^9,bi=0 or 1，bi=1的i的數量不超過400。

對於另外0%的數據：n≤100000，小喵喵會隨機地給每個小魚幹的屬性賦為-10^9≤ai,bi≤10^9。並且滿意度變為總滿意度=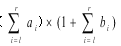

【提示】

請註意本題中的數字1與字母l的區別。（你可以根據需要縮放頁面比例）

其中。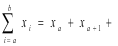

考試的時候看到這道題，我的內心是崩潰的。一個是因為對求和符號抱有自然的恐懼，另一個就是感覺數據量有點大。想了半天，最後還是用了前綴和+暴力，其中特殊考慮了一下全部a都為負的情況。得分60（也就是前12個點），後面的點時間超限。代碼如下：

 1 #include <iostream>
 2
 
 #include <cmath>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cstdlib>
 6 #include <algorithm>
 7 using namespace std;
 8 long long a[101010];
 9 int b[101010];
10 int main()
11 {
12     int n;
13     scanf("%d",&n);
14     bool ok=false;
15     a[0]=0;b[0]=0;
16     for(int i=1;i<=n;i++)
17     {
18      long long x;
19      scanf("%lld",&x);
20      a[i]=a[i-1]+x;
21      //printf("%lld  ",a[i]);
22      if(x>0) ok=true;
23     }
24     long long maxn=-999999999;
25     for(int i=1;i<=n;i++)
26     {
27      int y;
28      scanf("%d",&y);
29      if(!ok) maxn=max(maxn,(a[i]-a[i-1])*(y+1));
30      b[i]=b[i-1]+y;
31     }
32     if(!ok) {printf("%lld",maxn);return 0;}
33     long long ans=-999999999;
34     for(int i=1;i<=n;i++)
35     {
36         for(int j=0;j<i;j++)
37         {
38          long long sum=(a[i]-a[j])*(b[i]-b[j]+1);
39          ans=max(ans,sum);
40         }
41     }
42     printf("%lld",ans);
43     return 0; 
44 }

後來考完之後，我看了一些AC的代碼，發現他們的方法都驚人的相似。
他們都是記錄了b中1的位置，然後按1的位置把一長串數分為幾部分，然後：①在每段內求最大連續和；②考慮一段內b都是0的是否存在最大。

大神代碼如下：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstdlib>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<cmath>
 7 using namespace std;
 8 long long read()
 9 {
10     long long x=0,f=1;char ch=getchar();
11     while(!isdigit(ch)){if(ch==‘-‘) f=-1;ch=getchar();}
12     while(isdigit(ch)){x=x*10+ch-‘0‘;ch=getchar();}
13     return x*f;
14 }
15 long long n;
16 long long a[100001];
17 long long b[100001];
18 long long suma[100001],sumb[100001];  //前綴和 
19 long long add[500];  //(前一個1的位置，當前1的位置]中間的連續和最大值 
20 long long vis[500];  //b中值為1的數的位置 
21 long long cnt;
22 long long ans=0;
23 int main()
24 {
25     n=read();
26     for(int i=1;i<=n;i++){a[i]=read();suma[i]=suma[i-1]+a[i];}
27     for(int i=1;i<=n;i++){b[i]=read();sumb[i]=sumb[i-1]+b[i];if(b[i]==1) vis[++cnt]=i;}
28     memset(add,-97,sizeof(add));
29     vis[cnt+1]=n+1; //定義邊界 
30     for(int i=1;i<=cnt;i++)
31     {
32         long long temp=0;
33         for(int j=vis[i];j>vis[i-1];j--){temp+=a[j];add[i]=max(add[i],temp);} //找到每兩個1之間的最大聯系和 
34     }
35     for(int i=1;i<=n;i++) /*找到幾個連續段結合起來的最大*/
36     {
37         ans=max(ans,suma[i]*sumb[i]);  //乘積大於2^64是才會用得到高精度。本題不用 
38         for(int j=1;j<=sumb[i]/*有這麽多個1*/;j++)ans=max(ans,(add[j]+suma[i]-suma[vis[j]])*(sumb[i]-j+2)); //分段考慮取最大 
39     }
40     for(int i=0;i<=cnt;i++) /*以防某一段（b都是0）全部加起來是最大*/
41     {
42         long long w=0;
43         for(int j=vis[i]+1;j<vis[i+1];j++) {w=max(w+a[j],a[j]);ans=max(ans,w);}  //b全部為0的每段 
44     }
45     printf("%lld",ans);
46     return 0;
47 }

2017-HDNOIP-提高組1-小魚幹