2017282110288軟件工程第二次作業
一、Github項目地址:
https://github.com/VicLily/softwareEngineering
二、 PSP2.1表格:
|
PSP2.1 |
Personal Software Process Stages |
預估耗時(分鐘) |
實際耗時(分鐘) |
|
Planning |
計劃 |
30 |
60 |
|
· Estimate |
· 估計這個任務需要多少時間 |
30 |
60 |
|
Development |
開發 |
695 |
1130 |
|
· Analysis |
· 需求分析 (包括學習新技術) |
20 |
30 |
|
· Design Spec |
· 生成設計文檔 |
60 |
120 |
|
· Design Review |
· 設計復審 (和同事審核設計文檔) |
20 |
20 |
|
· Coding Standard |
· 代碼規範 (為目前的開發制定合適的規範) |
10 |
10 |
|
· Design |
· 具體設計 |
40 |
60 |
|
· Coding |
· 具體編碼 |
400 |
700 |
|
· Code Review |
· 代碼復審 |
30 |
50 |
|
· Test |
· 測試(自我測試,修改代碼,提交修改) |
120 |
100 |
|
Reporting |
報告 |
80 |
80 |
|
· Test Report |
· 測試報告 |
30 |
20 |
|
· Size Measurement |
· 計算工作量 |
20 |
20 |
|
· Postmortem & Process Improvement Plan |
· 事後總結, 並提出過程改進計劃 |
30 |
40 |
|
合計 |
|
810 |
1230 |
三、解題思路:
已實現功能:
· 運算符個數、類型、順序隨機生成。
· 操作數隨機生成。
· 用戶輸入題目個數,總分100分,每做完一個題判斷對錯後輸出正確答案。最後給出總分。
· 支持有括號的復合運算(在第二版中,但還存在有bug)
解題思路 :
代碼用java實現,另外需要導入JSON的包。
(1)在第一版的代碼實現中用了兩個集合類(運算符、操作數),所有整數、真分數分子分母分開存儲,通過遍歷這兩個集合類,先計算乘除,後計算加減。
(2)在第二版中用逆波蘭算法的思想,這裏建立了分子、分母、運算符三個基本棧,然後又建立其他工作棧進行輸出和運算操作。
因為剛開始沒有想太復雜,所以後來進行了改版,前面的實際時間為第一版的實際時間。
四、設計實現過程:
(1)
第一、首先定義全局變量M用以自定義運算符生成個數的上界,在1-M範圍內自動生成操作符的個數num。然後自動生成num+1個操作數,(分子和分母分別自動生成,其中分母不為0,這些數的取值範圍也是自定義)。
操作數的映射值是JSONObject類型的,分子和分母以Integer類型存儲在裏面。
第二、從頭遍歷一遍運算符的HashMap集合類,遇到乘號或者除號進行相應計算,然後把結果存儲到操作數集合DataList裏面,遇到加號或者減號則跳過。等到操作符的集合characterList遍歷完後乘和除運算已經做完,只剩下加和減操作。重新遍歷一遍characterList,計算加減運算。
第三、記兩個操作數的分子分母分別為zi1,mu1,zi2,mu2,記兩個操作數的計算結果為zi,mu。 操作數的四個值是DataList裏兩個JSONObject的對象的兩個獲取值。
當做加運算時:zi1/mu1 + zi2/mu2,分別計算分子和分母,mu=mu1*mu2,zi=zi1*mu2+zi2*mu1。將結果zi,mu約分後存儲在DataList
當做減運算時:zi1/mu1 - zi2/mu2,分別計算分子和分母,mu=mu1*mu2,zi=zi1*mu2-zi2*mu1。將結果zi,mu約分後存儲在DataList
當做乘運算時:zi1/mu1 * zi2/mu2,分別計算分子和分母,mu=mu1*mu2,zi=zi1*zi2。將結果zi,mu約分後存儲在DataList
當做除運算時:zi1/mu1 ÷ zi2/mu2,計算之前先做一個判斷,如果除號後面的操作數分子為0,則重新隨機生成一個不為0的數。分別計算分子和分母,mu=mu1*zi2,zi=zi1*mu2。將結果zi,mu約分後存儲在DataList
第四、在第一次遍歷characterList做完乘除操作後,記錄下不會再用到的操作符和操作數,然後刪除掉,再進行加減操作,加減操作完成後同樣刪除掉不會再用到的運算符和操作數。最後DataList只剩下最後的結果。將最後結果變成字符串的形式與用戶輸入的進行比較,如果匹配輸出“回答正確”,加上相應的分數。
(2)
在第二版中用逆波蘭算法,也是在第一版的基礎上做了修改,先建立分子、分母、操作符、括號的集合,隨機生成括號對數(1-2對),確定第一個左括號的位置,然後將括號和操作符依次入棧(同一個棧)分子分母分別入棧,然後進行出棧、判斷、計算、入棧等一系列操作。最後分子和分母的棧中就是最後的結果,將最後結果變成字符串類型與用戶輸入的進行比較,判斷對錯。(第二版中的計算部分與第一版的思想一致,但由於時間關系,目前在判斷上還存在bug需要調試修改)
五、代碼說明:
(1)第一版:
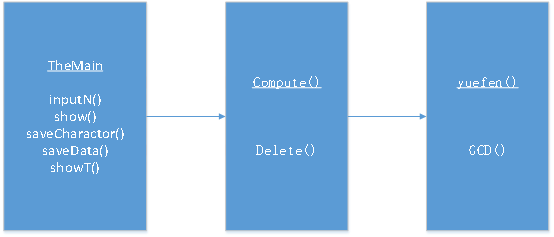
建立了三個.java文件,首先在TheMain類中,有5個內部類,inputN()用來處理用戶輸入有幾個題目,調用show()方法。Show()方法用來顯示有滿分、每道題目分數、運行saveCharactor()和saveData()方法,循環調用showT()方法和compute()類。
其中saveCharactor()和saveData()方法用來自動生成並存儲運算符和操作數。
ShowT()方法用來在控制臺輸出一個題目給用戶。
Compute()類用來計算對應運算符的運算操作,其中用Delete()方法刪除計算過不會再使用的運算符和操作數。
Yuefen()類用於對分子和分母的約分,GCD()方法是對分子和分母求最大公約數。
關鍵代碼:
下圖中代碼是輸出除號之前,判斷除號後面的操作數是否為0,若為0則重新隨機生成一個不為0的真分數存儲並輸出。

下圖代碼為隨機生成運算符的類型,其中num為自定義操作符個數的全局變量。

(2)第二版:
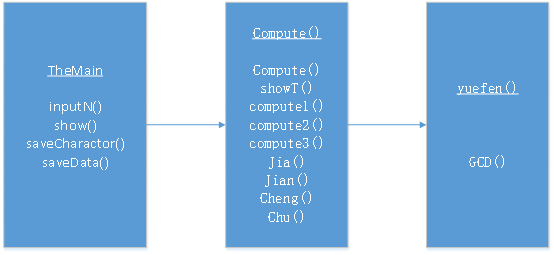
同第一版一樣,有三個.java文件。TheMain()類中的方法、yuefen()類與第一版的功能一樣。
Compute()類中,compute()方法用來自動生成括號個數以及確定括號的起始位置、調用showT()方法和compute1()方法。
showT()方法用來將自動生成的多項式顯示到控制臺中,並將集合中的數據和符號入棧。
Compute1()方法用來判斷每個出棧的符號,調用compute2對每個符號進行處理。(目前bug主要出現在這個方法裏,一些判斷還存在問題)。
Compute2()方法用來對加減乘除符號調用對應的jia()、jian()、cheng()、chu()運算操作。
Compute3()用來處理括號裏的運算。
jia()、jian()、cheng()、chu()方法和第一版的加減乘除運算的思想一致。
關鍵代碼:
主要為:根據運算符的個數確定括號的對數的範圍。如果只有一個運算符,不會生成括號。如果有兩個運算符,隨機生成0-1對括號。如果有3個以上的運算符,則生成0-2對括號。

六、測試運行:
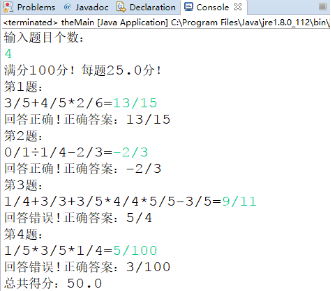
(1)運行結果:
第一版:
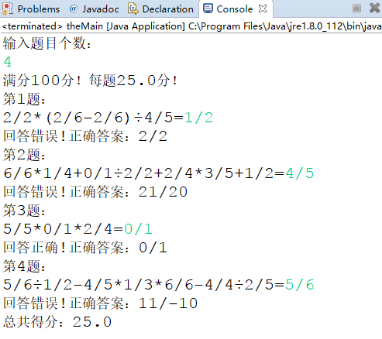
第二版:
(2)單元測試:
建立一個computeTest的單元測試類,對帶括號的compute類進行單元測試,測試代碼如下:
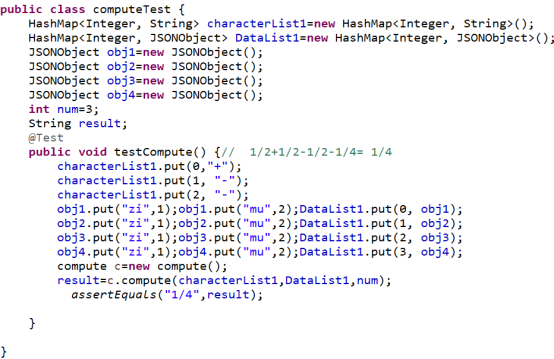
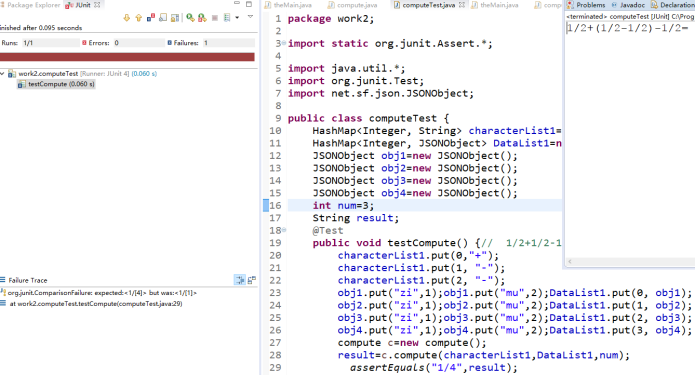
運行過後:由於括號自動生成,所以和手動輸入的結果不匹配,導致測試失敗。
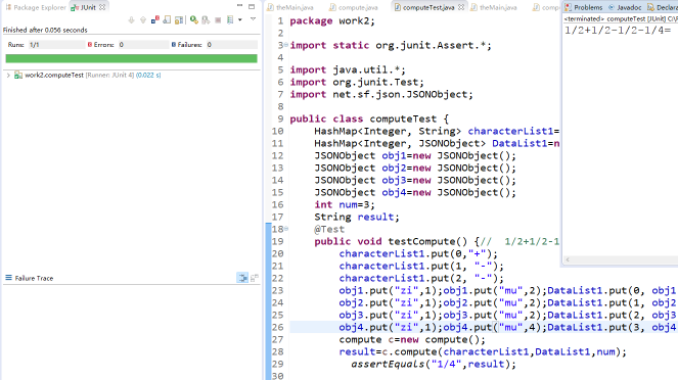
當沒有自動生成括號時,運行成功。
七、項目小結
我先看了《構建之法》的前幾章,看題目後感覺並沒有那麽難,然而在實際做的過程中卻遇到了很多問題,我覺得最要緊的就是剛開始構建思路的時候,可能由於經驗不足,走了很多彎路,不過結果還算正確運行了出來,等到加括號的運算時候,發現自己之前寫的並不是好的代碼,不簡潔、不清晰,也沒有將設計模式運用出來,我覺得可能還需要更多的項目經驗來提高編碼的能力。
2017282110288軟件工程第二次作業
