算法分析和具體步驟解說直接寫在代碼註釋上了

TvT 沒時間了等下還要去洗衣服 就先不贅述了

有不明白的歡迎留言交流！（估計是沒人看的了）

直接上代碼：

  1 #include<stdio.h>
  2 #include<queue>
  3 #include<iostream>
  4 using namespace std;
  5 typedef struct{
  6 int Vex[10];//頂點表
  7 int Edge[10][10];
  8 int vexnum,arcnum;
  9 }MGraph;
 10 bool visited[10
 
];
 11 void printGraph(MGraph &G)
 12 {
 13     cout<<"Show the Graph."<<endl;
 14     cout<<"----------------------------"<<endl;
 15     for(int i=0;i<10;i++){
 16         for(int j=0;j<10;j++)
 17     {
 18         cout<<" "<<G.Edge[i][j]<<" ";
 19     }
 
 20     cout<<endl;
 21     }
 22     cout<<"----------------------------"<<endl;
 23     cout<<"There are "<<G.arcnum<<" arcs in the Graph!"<<endl;
 24     cout<<"Arcs are listed as follow:"<<endl;
 25     for(int i=0;i<10;i++){
 26         for(int
 
 j=0;j<10;j++)
 27     {
 28         if(G.Edge[i][j]==1)
 29             cout<<i<<"-->"<<j<<endl;
 30     }
 31     }
 32 }
 33 int initGraph(MGraph &G)
 34 {
 35     G.vexnum=10;
 36     G.arcnum=0;
 37     for(int i=0;i<10;i++)
 38         for(int j=0;j<10;j++)
 39     {
 40         G.Edge[i][j]=0;
 41     }
 42     cout<<"input the relation of a pair of dots (A,B) to build a graph.(0<A,B<10)"<<endl;
 43     cout<<"End up with data(0,0)"<<endl;
 44     int a,b;
 45     cin>>a>>b;
 46     while(a!=0&&b!=0){
 47     G.arcnum++;
 48     G.Edge[a][b]=1;
 49     cin>>a>>b;
 50     }
 51     cout<<"successful."<<endl;
 52     printGraph(G);
 53 }
 54 bool isNeibour(MGraph &G,int a,int b)
 55 {
 56     if(G.Edge[a][b]==1)
 57         return true;
 58     else return false;
 59 }
 60 int firstNeighbor(MGraph &G,int v)
 61 {
 62     int pos=-1;
 63     for(int i=0;i<G.vexnum;i++)
 64     {
 65         if((G.Edge[v][i]==1))
 66             {pos=i;break;}
 67     }
 68     return pos;
 69 }
 70 int nextNeighbor(MGraph &G,int v,int w)
 71 {
 72     int pos=-1;
 73     for(int i=w+1;i<G.vexnum;i++)
 74     {
 75         if((G.Edge[v][i]==1))
 76         {
 77             pos=i;break;
 78         }
 79     }
 80     return pos;
 81 }
 82 void visit(int v)
 83 {
 84     visited[v]=true;
 85     cout<<v<<" ";
 86 }
 87 queue<int> Q;
 88 void bfs(MGraph G,int v)
 89 {
 90     visit(v);
 91     Q.push(v);
 92     int now;
 93     while(!Q.empty())
 94     {
 95         now=Q.front();
 96         Q.pop();
 97         for(int w=firstNeighbor(G,now);w>=0;w=nextNeighbor(G,now,w))
 98         {
 99             if(!visited[w])
100             {
101                 visit(w);
102                 Q.push(now);
103             }
104         }
105     }
106 }
107 void BFS(MGraph &G)
108 {
109     for(int i=0;i<G.vexnum;i++)
110         visited[i]=false;
111     for(int i=0;i<G.vexnum;i++)
112     {
113         if(!visited[i])
114             bfs(G,i);
115     }
116 }
117 /*DFS 深度優先搜索*/
118 /*類似於樹的先序遍歷
119 其搜索策略：盡可能【深】地搜索一個圖。
120 遍歷思想：
121 從一個起始頂點v出發，訪問與v鄰接但未被訪問的任一頂點a→繼續訪問a頂點的下一未被訪問的頂點b→……→無法再向下訪問時依次退回到最近被訪問的頂點
122 直到所有頂點都被訪問為止
123 */
124 void dfs(MGraph &G,int v)
125 {
126     visit(v);
127     int w;
128     for(w=firstNeighbor(G,v);w>=0;w=nextNeighbor(G,v,w))
129     {
130         if(!visited[w])
131         {
132             dfs(G,w);
133         }
134     }
135 }
136 void DFS(MGraph &G)
137 {
138     for(int i=0;i<G.vexnum;i++)
139     {
140         visited[i]=false;
141     }
142     for(int i=0;i<G.vexnum;i++)
143     {
144         if(!visited[i])
145             dfs(G,i);
146     }
147 }
148 int main()
149 {
150     MGraph P;
151     initGraph(P);
152     cout<<"test of BFS:"<<endl;
153     BFS(P);
154     cout<<endl;
155     cout<<"test of DFS:"<<endl;
156     DFS(P);
157     return 0;
158 }

附一張運行截圖

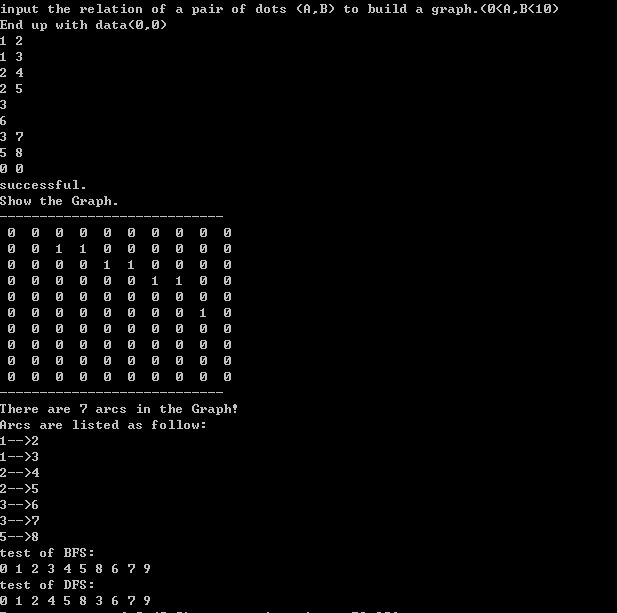
15 圖-圖的遍歷-基於鄰接矩陣實現的BFS與DFS算法