廣度優先遍歷是連通圖的一種遍歷策略。其基本思想如下：

1、從圖中某個頂點V0出發，並訪問此頂點；

2、從V0出發，訪問V0的各個未曾訪問的鄰接點W1，W2，…,Wk;然後,依次從W1,W2,…,Wk出發訪問各自未被訪問的鄰接點；

3、重複步驟2，直到全部頂點都被訪問為止。

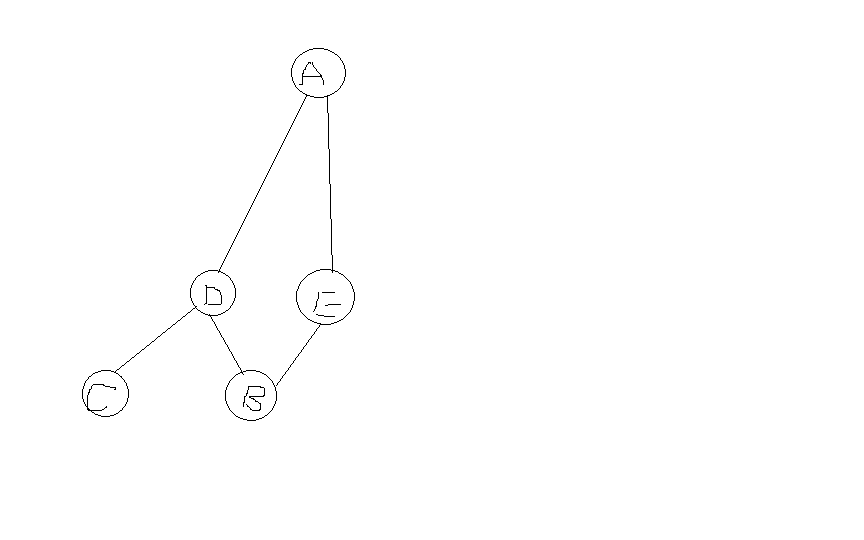
例如下圖中：

1.從A開始，首先找到A的關聯頂點D,E

2.由D出發，找到B，C；由E出發，找到A，但是A已經遍歷過，所以忽略。

3.由B出發，沒有關聯頂點；由C出發，沒有關聯頂點。

所以最後順序是A,D,E,B,C
0 0 0 1 1
0 0 0 1 1
0 0 0 1 0
1 1 1 0 0
1 1 0 0 0
c語言實現如下：（使用鄰接矩陣儲存）

include”stdio.h”

include”stdlib.h”

define MAX_SIZE 10

typedef char Elemtype;
typedef int status;
//建立佇列 
typedef struct QNode{
Elemtype data;
QNode *next;        
}QNode,*Queueptr;
typedef struct{
Queueptr front,rear;
}LinkQueue; 
//圖的結構體 
typedef struct{
int vexnum;//結點數量 
Elemtype vex[MAX_SIZE];//結點資料 
int cmb[MAX_SIZE][MAX_SIZE];//各節點間的聯絡 
}Graph;
status initQueue(LinkQueue &Q)
{
Q.front = Q.rear = (Queueptr)malloc(sizeof(QNode));
if(!Q.front)
{
    exit(0);
}
Q.front->next = NULL;  
return 0;
}
status enQueue(LinkQueue &Q,Elemtype c)
{
Queueptr p = (Queueptr)malloc(sizeof(QNode));
if(!p) exit(0);
p->data = c;
p->next = NULL;
Q.rear->next = p;
Q.rear = p;
return 0;
}
status deQueue(LinkQueue &Q,Elemtype &c)
{
Queueptr p = Q.front->next;
c = p->data;
Q.front->next = p->next;
if(Q.rear == p) Q.rear = Q.front;
free(p);
return 0; 
}
status emptyQueue(LinkQueue Q)
{
if(Q.front != Q.rear)
{
    return 0;
}
else return 1;

}
int main()
{
LinkQueue Q;
initQueue(Q);
Elemtype c,e;
Graph G;
int n,visit[MAX_SIZE],i,j;
printf("請輸入圖結點數量:\n");
scanf("%d",&n);
scanf("%c",&e);//接收回車 
for(int i = 0;i<n;i++)
    visit[i] = false;
G.vexnum = n;
printf("輸入資料：\n");
for(i=0;i<G.vexnum;i++)
{
    scanf("%c",&G.vex[i]);

}
scanf("%c",&e);//接收回車 
printf("請輸入圖頂點之間的關係(下三角)：\n");
for( i = 0;i<G.vexnum;i++)
{
    for( j = 0;j<=i;j++)
    {
        scanf("%d",&G.cmb[i][j]);
        G.cmb[j][i] = G.cmb[i][j];
    }
}
//核心程式碼塊
for(i=0;i<G.vexnum;i++)
{
    if(!visit[i]) 
    {
    visit[i] = true;
    enQueue(Q,G.vex[i]);
    while(!emptyQueue(Q))
    {
        deQueue(Q,c);//出棧 
        printf("%2c",c);
        for(j=0;j<G.vexnum;j++)//出棧元素的下一層元素入棧 
        {
            if(G.cmb[i][j]&&!visit[j])
            {
                visit[j] = true;
                enQueue(Q,G.vex[j]);

            }
        }
    }
}
//核心程式碼塊
}
}
 

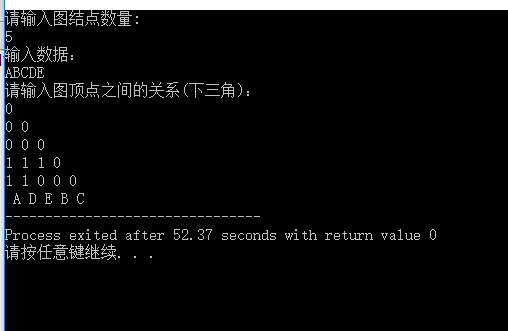
執行結果