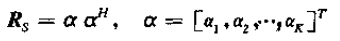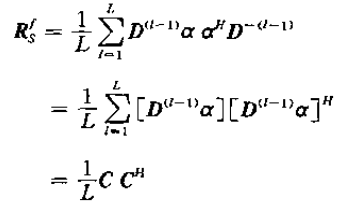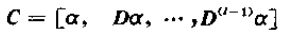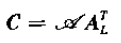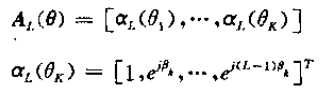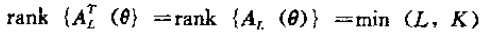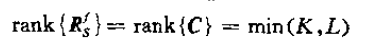作者：桂。

時間：2017-09-29 21:20:18

鏈接：http://www.cnblogs.com/xingshansi/p/7612984.html

未完待續。。。

前言

主要分析在解相幹算法中，子陣平滑的有效性。

一、前向平滑

以均勻線陣（ULA）為例，第l個接收陣元的信號為：

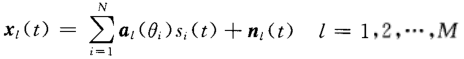
其中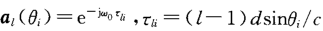，M為陣元數，N為信號個數。

以前向平滑為例：

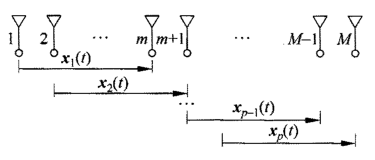
令β = 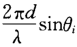，對於第k個子陣有

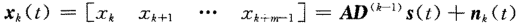
其中D為:

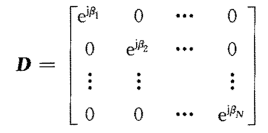
假設信號與噪聲不相關，且噪聲為白噪聲，計算相關矩陣：

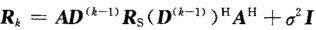
前向平滑修正的協方差矩陣：

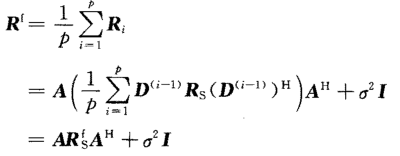
證明：當子陣陣元數m>=N，且當p>=N時，Rf為滿秩矩陣。

對於相幹情況，Rs的秩為1，故可以用矢量相乘的形式表示：

則

顯然C與R_sf的秩是一致的。式中

C可進一步表示為

其中，α為對應信號的幅度，因此該矩陣rank = K

A_L是Vandermonde矩陣：

從而有：

進一步得出結論：

得證。

上面的推導是教科書中的推導，以兩個子陣、兩個信號為例，假設兩個子陣的間距為D，對應的A可寫為：

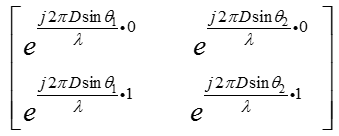
雖然具有Vandermonde結構，但即使入射角度不同，上面的矩陣仍然可能出現rank = 1的情況，只要滿足（k為整數）：

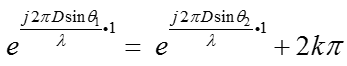
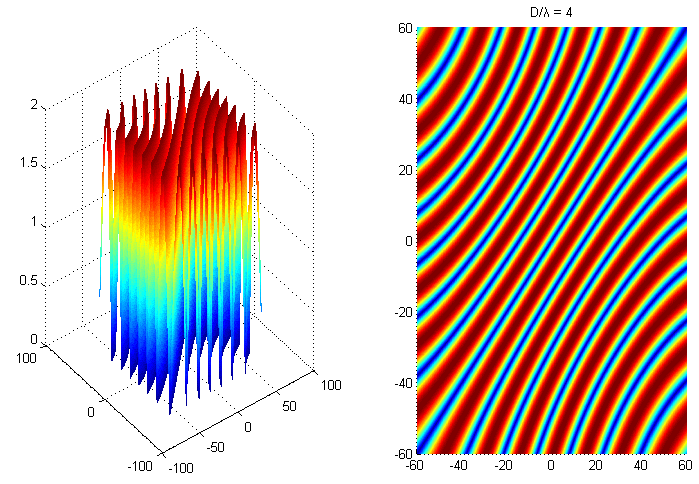
任意取D = 4*λ，theta1、2分別取-60°~60°，仿真結果：

D = 2*λ，進行仿真：

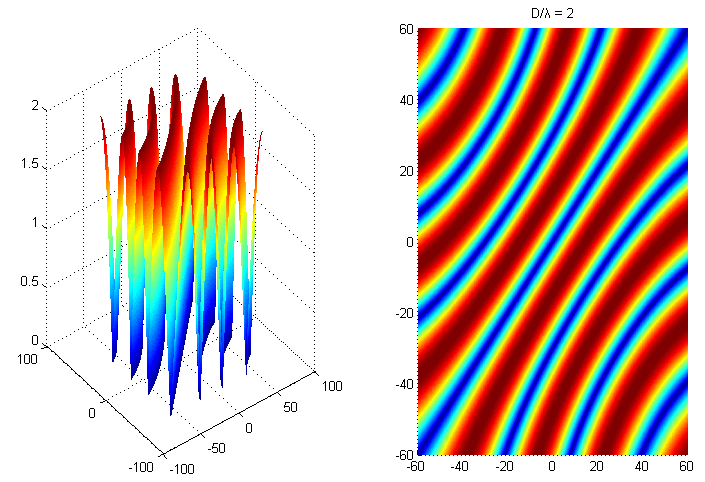
當兩個相位差2pi整數倍，如圖藍線所示，此時相關矩陣的秩仍然是虧缺的，此時譜估計解相幹失效，這裏稱藍色區域為盲區。以MUSIC算法為例，自然也無從談起矩陣分解以及譜估計。另一方面，D與λ比值的取值越小，則盲區越小。

二、後向平滑算法

三、前後向平滑算法

四、前向、後向、前後向平滑與陣列的關系

五、前後向與非均勻的關系

六、非均勻鏡像中坐標點的影響

主要影響D，近而影響盲區

空間譜專題11：子陣平滑與秩虧缺