8大排序算法圖文講解
排序有內部排序和外部排序,內部排序是數據記錄在內存中進行排序,而外部排序是因排序的數據很大,一次不能容納全部的排序記錄,在排序過程中需要訪問外存。
我們這裏說說八大排序就是內部排序。
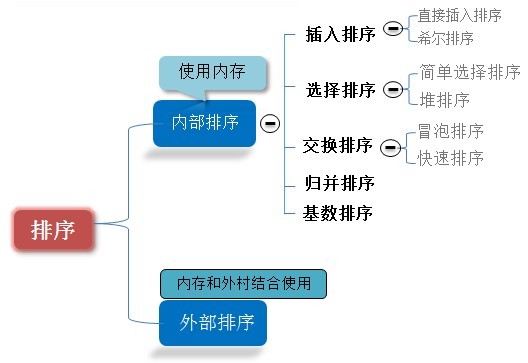
當n較大,則應采用時間復雜度為O(nlog2n)的排序方法:快速排序、堆排序或歸並排序序。
快速排序:是目前基於比較的內部排序中被認為是最好的方法,當待排序的關鍵字是隨機分布時,快速排序的平均時間最短;
算法一:插入排序

插入排序示意圖
插入排序是一種最簡單直觀的排序算法,它的工作原理是通過構建有序序列,對於未排序數據,在已排序序列中從後向前掃描,找到相應位置並插入。
算法步驟:
1)將第一待排序序列第一個元素看做一個有序序列,把第二個元素到最後一個元素當成是未排序序列。
2)從頭到尾依次掃描未排序序列,將掃描到的每個元素插入有序序列的適當位置。(如果待插入的元素與有序序列中的某個元素相等,則將待插入元素插入到相等元素的後面。)
代碼實現:
1 public class InsertSort { 2 3 public static void sort(int[] num){ 4 int i,j,min,temp; 5 for(i=0;i<num.length;i++){ 6 min=i;//將當前下標定義為最小值下標 7 for(j=i+1;j<num.length;j++){8 if (num[min]>num[j]) { 9 min=j;//如果有小於當前最小值的關鍵字,將此關鍵字的下標賦值給min 10 } 11 } 12 if (i!=min) {//若min不等於i,說明上面相互比較的為true,即有最小值,交換 13 temp=num[i]; 14 num[i]=num[min]; 15 num[min]=temp;16 } 17 } 18 for (int k : num) { 19 System.out.println(k); 20 } 21 22 } 23 24 25 public static void main(String[] args) { 26 // TODO 自動生成的方法存根 27 int[] num={5,2,4,6,8,9,7,1,3,0}; 28 sort(num); 29 } 30 }
算法二:希爾排序

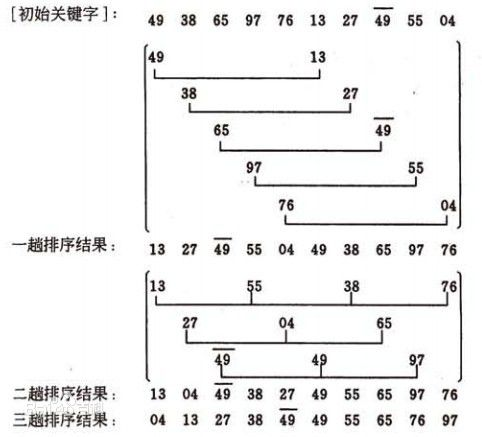
給定實例的shell排序的排序過程 假設待排序文件有10個記錄,其關鍵字分別是: 49,38,65,97,76,13,27,49,55,04。 增量序列的取值依次為: 5,3,1
希爾排序,也稱遞減增量排序算法,是插入排序的一種更高效的改進版本。但希爾排序是非穩定排序算法。
希爾排序是基於插入排序的以下兩點性質而提出改進方法的:
- 插入排序在對幾乎已經排好序的數據操作時, 效率高, 即可以達到線性排序的效率
- 但插入排序一般來說是低效的, 因為插入排序每次只能將數據移動一位
希爾排序的基本思想是:先將整個待排序的記錄序列分割成為若幹子序列分別進行直接插入排序,待整個序列中的記錄“基本有序”時,再對全體記錄進行依次直接插入排序。
算法步驟:
1)選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
2)按增量序列個數k,對序列進行k 趟排序;
3)每趟排序,根據對應的增量ti,將待排序列分割成若幹長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
代碼實現:
1 public class ShellSort { 2 //希爾排序 3 public static void sort(int[] a) { 4 // 希爾排序 5 int d = a.length; 6 while (true) { 7 d = d / 2; 8 for (int x = 0; x < d; x++) { 9 for (int i = x + d; i < a.length; i = i + d) { 10 int temp = a[i]; 11 int j; 12 for (j = i - d; j >= 0 && a[j] > temp; j = j - d) { 13 a[j + d] = a[j]; 14 } 15 a[j + d] = temp; 16 } 17 } 18 if (d == 1) { 19 break; 20 } 21 } 22 23 for (int k : a) { 24 System.out.println(k); 25 } 26 } 27 28 public static void main(String[] args) { 29 // TODO Auto-generated method stub 30 int[] a = { 5, 2, 4, 6, 8, 9, 7, 1, 3, 0 }; 31 // int[]a={49,38,65,97,76,13,27,49,78,34,12,64,1}; 32 sort(a); 33 } 34 35 }
算法三:選擇排序

選擇排序示意圖
選擇排序(Selection sort)也是一種簡單直觀的排序算法。
算法步驟:
1)首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
2)再從剩余未排序元素中繼續尋找最小(大)元素,然後放到已排序序列的末尾。
3)重復第二步,直到所有元素均排序完畢。
代碼實現:
1 /** 2 * 選擇一個min做基準和其他的數據相互比較,如果比較的數大則把當前的數的賦值給min 3 * 以此類推 4 * @author Administrator 5 * 6 */ 7 public class SelectSort { 8 //簡單選擇排序,選擇一個min做基準和其他的數據相互比較 9 public static void sort(int[] num){ 10 int i,j,min,temp; 11 for(i=0;i<num.length;i++){ 12 min=i;//將當前下標定義為最小值下標 13 for(j=i+1;j<num.length;j++){ 14 if (num[min]>num[j]) { 15 min=j;//如果有小於當前最小值的關鍵字,將此關鍵字的下標賦值給min 16 } 17 } 18 if (i!=min) {//若min不等於i,說明上面相互比較的為true,即有最小值,交換 19 temp=num[i]; 20 num[i]=num[min]; 21 num[min]=temp; 22 } 23 } 24 for (int k : num) { 25 System.out.println(k); 26 } 27 28 } 29 30 public static void main(String args[]){ 31 int[] num={5,2,4,6,8,9,7,1,3,0}; 32 sort(num); 33 34 } 35 }
算法四:冒泡排序

冒泡排序示意圖
冒泡排序(Bubble Sort)也是一種簡單直觀的排序算法。它重復地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重復地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列的頂端。
算法步驟:
1)比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
2)對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。這步做完後,最後的元素會是最大的數。
3)針對所有的元素重復以上的步驟,除了最後一個。
4)持續每次對越來越少的元素重復上面的步驟,直到沒有任何一對數字需要比較。
代碼實現:
1 /** 2 * 相鄰數據兩兩比較,大的排上面,小的排下面 第一次可排出最小的值 3 * 第二次排出第二小的值 4 * 第三次排出第三小的值 5 * 以此類推排出順序 6 * @author Administrator 7 * 8 */ 9 public class BubbleSort { 10 11 //初級版 12 public static void sort1(int[] num){ 13 int i,j,temp; 14 for(i=0;i<num.length;i++){ 15 for(j=i+1;j<num.length;j++){ 16 if (num[i]>num[j]) { 17 temp=num[i]; 18 num[i]=num[j]; 19 num[j]=temp; 20 } 21 } 22 } 23 for (int k : num) { 24 System.out.println(k); 25 } 26 27 } 28 //中級版 29 public static void sort2(int[] num){ 30 int i,j,temp; 31 for(i=0;i<num.length;i++){ 32 for(j=num.length-1;j>i;j--){ 33 if (num[j-1]>num[j]) { 34 temp=num[j-1]; 35 num[j-1]=num[j]; 36 num[j]=temp; 37 } 38 } 39 } 40 for (int k : num) { 41 System.out.println(k); 42 } 43 44 } 45 //終極版 46 public static void sort3(int[] num){ 47 int i,j,temp; 48 boolean flag=true; 49 for(i=0;i<num.length&&flag;i++){ 50 flag=false; 51 for(j=num.length-1;j>i;j--){ 52 if (num[j-1]>num[j]) { 53 temp=num[j-1]; 54 num[j-1]=num[j]; 55 num[j]=temp; 56 flag=true; 57 } 58 } 59 } 60 for (int k : num) { 61 System.out.println(k); 62 } 63 64 } 65 66 67 public static void main(String args[]){ 68 int[] num={5,2,4,6,8,9,7,1,3,0}; 69 // sort1(num); 70 // sort2(num); 71 sort3(num); 72 } 73 74 }
算法五:歸並排序

歸並排序示意圖
歸並排序(MERGE-SORT)是利用歸並的思想實現的排序方法,該算法采用經典的分治(divide-and-conquer)策略(分治法將問題分(divide)成一些小的問題然後遞歸求解,而治(conquer)的階段則將分的階段得到的各答案"修補"在一起,即分而治之)。
分而治之

可以看到這種結構很像一棵完全二叉樹,本文的歸並排序我們采用遞歸去實現(也可采用叠代的方式去實現)。分階段可以理解為就是遞歸拆分子序列的過程,遞歸深度為log2n。
合並相鄰有序子序列
再來看看治階段,我們需要將兩個已經有序的子序列合並成一個有序序列,比如上圖中的最後一次合並,要將[4,5,7,8]和[1,2,3,6]兩個已經有序的子序列,合並為最終序列[1,2,3,4,5,6,7,8],來看下實現步驟。
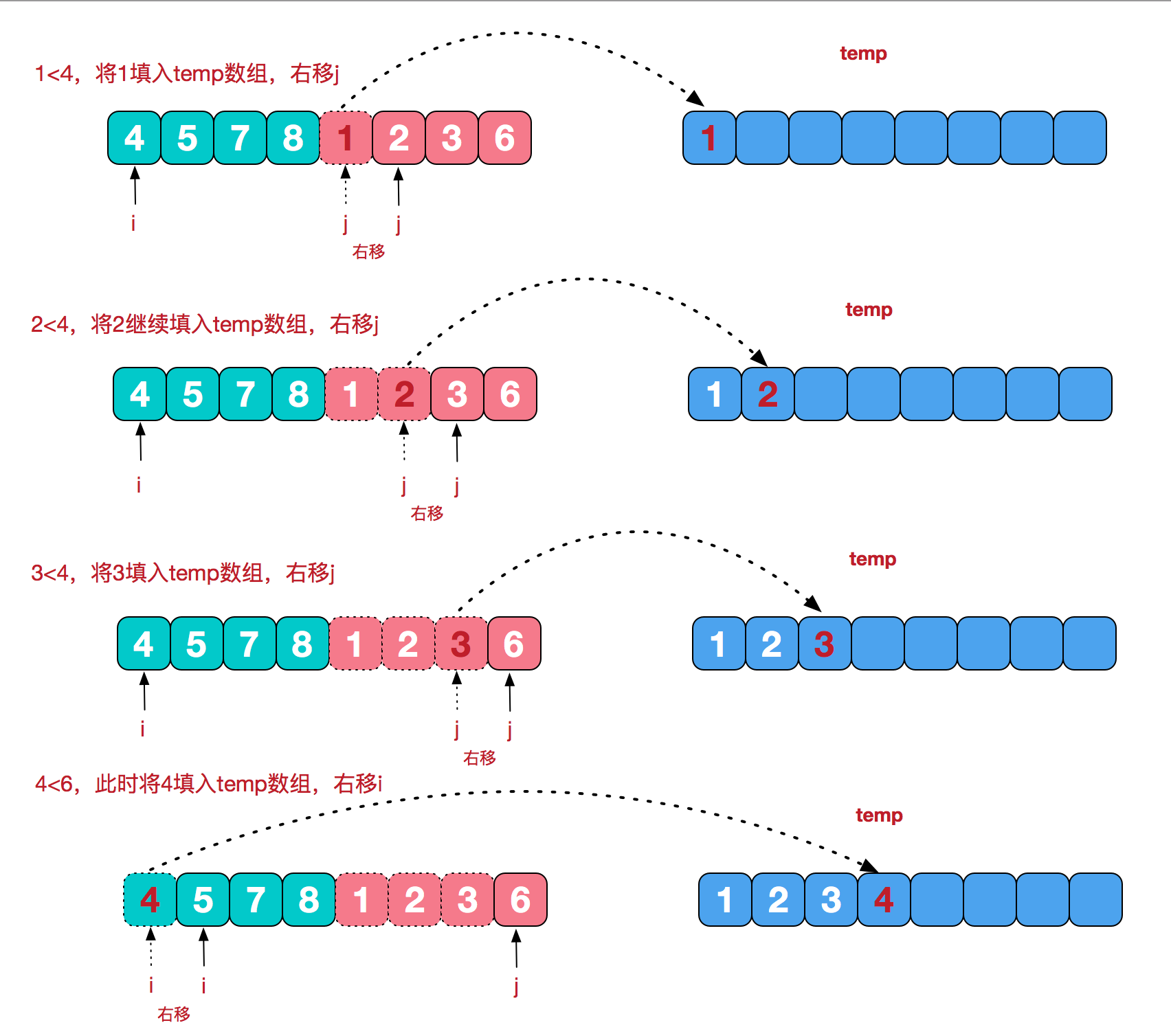
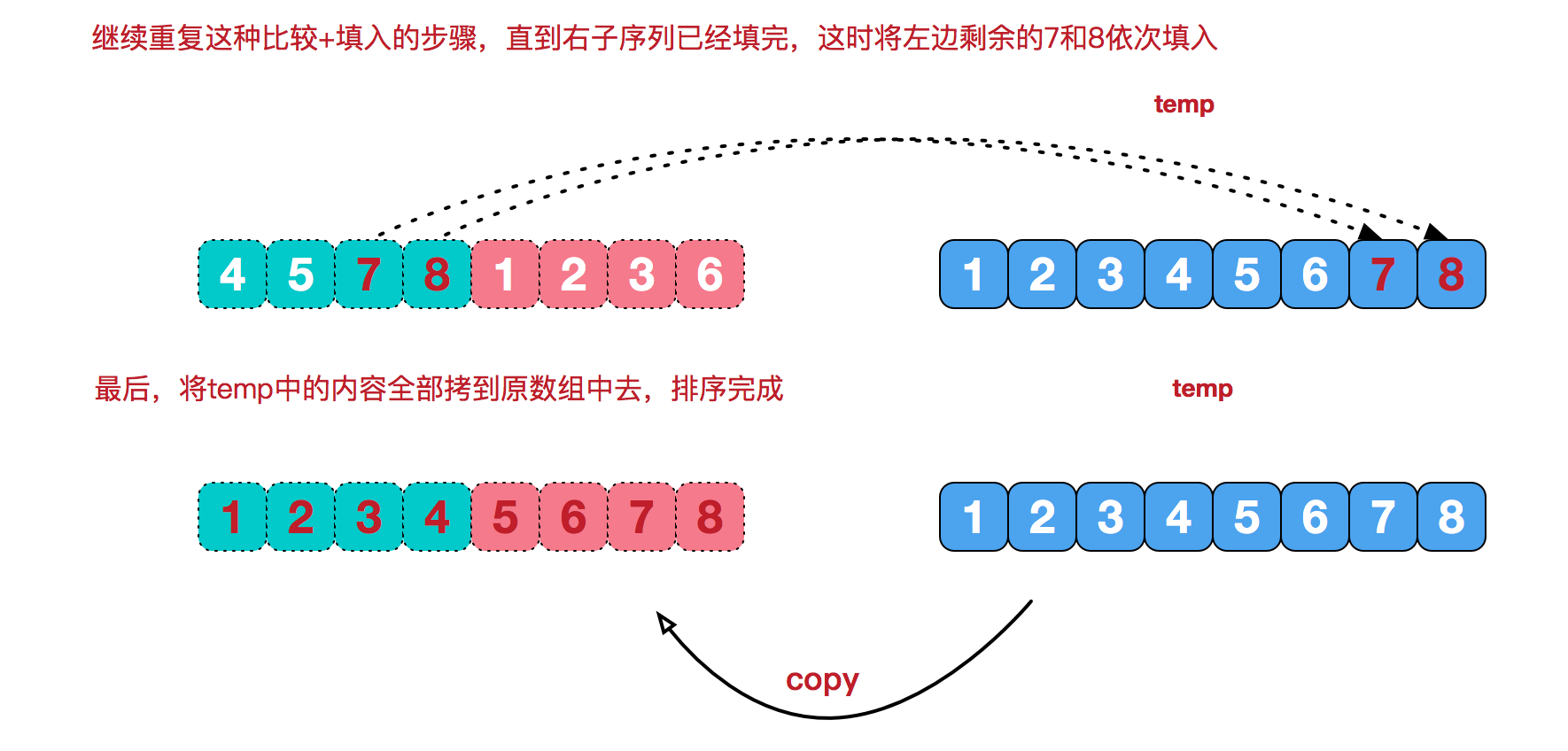
代碼實現

package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/8.
*/
public class MergeSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
int []temp = new int[arr.length];//在排序前,先建好一個長度等於原數組長度的臨時數組,避免遞歸中頻繁開辟空間
sort(arr,0,arr.length-1,temp);
}
private static void sort(int[] arr,int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;
sort(arr,left,mid,temp);//左邊歸並排序,使得左子序列有序
sort(arr,mid+1,right,temp);//右邊歸並排序,使得右子序列有序
merge(arr,left,mid,right,temp);//將兩個有序子數組合並操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;//左序列指針
int j = mid+1;//右序列指針
int t = 0;//臨時數組指針
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//將左邊剩余元素填充進temp中
temp[t++] = arr[i++];
}
while(j<=right){//將右序列剩余元素填充進temp中
temp[t++] = arr[j++];
}
t = 0;
//將temp中的元素全部拷貝到原數組中
while(left <= right){
arr[left++] = temp[t++];
}
}
}

執行結果
[1, 2, 3, 4, 5, 6, 7, 8, 9]
最後
歸並排序是穩定排序,它也是一種十分高效的排序,能利用完全二叉樹特性的排序一般性能都不會太差。java中Arrays.sort()采用了一種名為TimSort的排序算法,就是歸並排序的優化版本。從上文的圖中可看出,每次合並操作的平均時間復雜度為O(n),而完全二叉樹的深度為|log2n|。總的平均時間復雜度為O(nlogn)。而且,歸並排序的最好,最壞,平均時間復雜度均為O(nlogn)。
8大排序算法圖文講解
