poj1673 EXOCENTER OF A TRIANGLE
阿新 • • 發佈:2017-10-12
call atan nbsp original nec cte rec cat ace
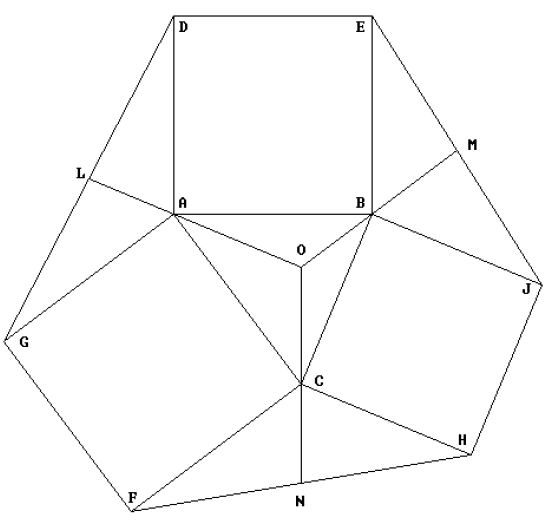
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).
地址:http://poj.org/problem?id=1673
題目:
EXOCENTER OF A TRIANGLE| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 3637 | Accepted: 1467 |
Description
Given a triangle ABC, the Extriangles of ABC are constructed as follows:On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).

Input
The first line of the input consists of a positive integer n, which is the number of datasets that follow. Each dataset consists of 3 lines; each line contains two floating point values which represent the (two -dimensional) coordinate of one vertex of a triangle. So, there are total of (n*3) + 1 lines of input. Note: All input triangles wi ll be strongly non-degenerate in that no vertex will be within one unit of the line through the other two vertices.Output
Sample Input
2 0.0 0.0 9.0 12.0 14.0 0.0 3.0 4.0 13.0 19.0 2.0 -10.0
Sample Output
9.0000 3.7500 -48.0400 23.3600
Source
Greater New York 2003 思路: 其實就是重心。1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 #include <algorithm> 5 6 7 using namespace std; 8 const double PI = acos(-1.0); 9 const double eps = 1e-10; 10 11 /****************常用函數***************/ 12 //判斷ta與tb的大小關系 13 int sgn( double ta, double tb) 14 { 15 if(fabs(ta-tb)<eps)return 0; 16 if(ta<tb) return -1; 17 return 1; 18 } 19 20 //點 21 class Point 22 { 23 public: 24 25 double x, y; 26 27 Point(){} 28 Point( double tx, double ty){ x = tx, y = ty;} 29 30 bool operator < (const Point &_se) const 31 { 32 return x<_se.x || (x==_se.x && y<_se.y); 33 } 34 friend Point operator + (const Point &_st,const Point &_se) 35 { 36 return Point(_st.x + _se.x, _st.y + _se.y); 37 } 38 friend Point operator - (const Point &_st,const Point &_se) 39 { 40 return Point(_st.x - _se.x, _st.y - _se.y); 41 } 42 //點位置相同(double類型) 43 bool operator == (const Point &_off)const 44 { 45 return sgn(x, _off.x) == 0 && sgn(y, _off.y) == 0; 46 } 47 48 }; 49 50 /****************常用函數***************/ 51 //點乘 52 double dot(const Point &po,const Point &ps,const Point &pe) 53 { 54 return (ps.x - po.x) * (pe.x - po.x) + (ps.y - po.y) * (pe.y - po.y); 55 } 56 //叉乘 57 double xmult(const Point &po,const Point &ps,const Point &pe) 58 { 59 return (ps.x - po.x) * (pe.y - po.y) - (pe.x - po.x) * (ps.y - po.y); 60 } 61 //兩點間距離的平方 62 double getdis2(const Point &st,const Point &se) 63 { 64 return (st.x - se.x) * (st.x - se.x) + (st.y - se.y) * (st.y - se.y); 65 } 66 //兩點間距離 67 double getdis(const Point &st,const Point &se) 68 { 69 return sqrt((st.x - se.x) * (st.x - se.x) + (st.y - se.y) * (st.y - se.y)); 70 } 71 72 //兩點表示的向量 73 class Line 74 { 75 public: 76 77 Point s, e;//兩點表示,起點[s],終點[e] 78 double a, b, c;//一般式,ax+by+c=0 79 double angle;//向量的角度,[-pi,pi] 80 81 Line(){} 82 Line( Point ts, Point te):s(ts),e(te){}//get_angle();} 83 Line(double _a,double _b,double _c):a(_a),b(_b),c(_c){} 84 85 //排序用 86 bool operator < (const Line &ta)const 87 { 88 return angle<ta.angle; 89 } 90 //向量與向量的叉乘 91 friend double operator / ( const Line &_st, const Line &_se) 92 { 93 return (_st.e.x - _st.s.x) * (_se.e.y - _se.s.y) - (_st.e.y - _st.s.y) * (_se.e.x - _se.s.x); 94 } 95 //向量間的點乘 96 friend double operator *( const Line &_st, const Line &_se) 97 { 98 return (_st.e.x - _st.s.x) * (_se.e.x - _se.s.x) - (_st.e.y - _st.s.y) * (_se.e.y - _se.s.y); 99 } 100 //從兩點表示轉換為一般表示 101 //a=y2-y1,b=x1-x2,c=x2*y1-x1*y2 102 bool pton() 103 { 104 a = e.y - s.y; 105 b = s.x - e.x; 106 c = e.x * s.y - e.y * s.x; 107 return true; 108 } 109 //半平面交用 110 //點在向量左邊(右邊的小於號改成大於號即可,在對應直線上則加上=號) 111 friend bool operator < (const Point &_Off, const Line &_Ori) 112 { 113 return (_Ori.e.y - _Ori.s.y) * (_Off.x - _Ori.s.x) 114 < (_Off.y - _Ori.s.y) * (_Ori.e.x - _Ori.s.x); 115 } 116 //求直線或向量的角度 117 double get_angle( bool isVector = true) 118 { 119 angle = atan2( e.y - s.y, e.x - s.x); 120 if(!isVector && angle < 0) 121 angle += PI; 122 return angle; 123 } 124 125 //點在線段或直線上 1:點在直線上 2點在s,e所在矩形內 126 bool has(const Point &_Off, bool isSegment = false) const 127 { 128 bool ff = sgn( xmult( s, e, _Off), 0) == 0; 129 if( !isSegment) return ff; 130 return ff 131 && sgn(_Off.x - min(s.x, e.x), 0) >= 0 && sgn(_Off.x - max(s.x, e.x), 0) <= 0 132 && sgn(_Off.y - min(s.y, e.y), 0) >= 0 && sgn(_Off.y - max(s.y, e.y), 0) <= 0; 133 } 134 135 //點到直線/線段的距離 136 double dis(const Point &_Off, bool isSegment = false) 137 { 138 ///化為一般式 139 pton(); 140 //到直線垂足的距離 141 double td = (a * _Off.x + b * _Off.y + c) / sqrt(a * a + b * b); 142 //如果是線段判斷垂足 143 if(isSegment) 144 { 145 double xp = (b * b * _Off.x - a * b * _Off.y - a * c) / ( a * a + b * b); 146 double yp = (-a * b * _Off.x + a * a * _Off.y - b * c) / (a * a + b * b); 147 double xb = max(s.x, e.x); 148 double yb = max(s.y, e.y); 149 double xs = s.x + e.x - xb; 150 double ys = s.y + e.y - yb; 151 if(xp > xb + eps || xp < xs - eps || yp > yb + eps || yp < ys - eps) 152 td = min( getdis(_Off,s), getdis(_Off,e)); 153 } 154 return fabs(td); 155 } 156 157 //關於直線對稱的點 158 Point mirror(const Point &_Off) 159 { 160 ///註意先轉為一般式 161 Point ret; 162 double d = a * a + b * b; 163 ret.x = (b * b * _Off.x - a * a * _Off.x - 2 * a * b * _Off.y - 2 * a * c) / d; 164 ret.y = (a * a * _Off.y - b * b * _Off.y - 2 * a * b * _Off.x - 2 * b * c) / d; 165 return ret; 166 } 167 //計算兩點的中垂線 168 static Line ppline(const Point &_a,const Point &_b) 169 { 170 Line ret; 171 ret.s.x = (_a.x + _b.x) / 2; 172 ret.s.y = (_a.y + _b.y) / 2; 173 //一般式 174 ret.a = _b.x - _a.x; 175 ret.b = _b.y - _a.y; 176 ret.c = (_a.y - _b.y) * ret.s.y + (_a.x - _b.x) * ret.s.x; 177 //兩點式 178 if(fabs(ret.a) > eps) 179 { 180 ret.e.y = 0.0; 181 ret.e.x = - ret.c / ret.a; 182 if(ret.e == ret. s) 183 { 184 ret.e.y = 1e10; 185 ret.e.x = - (ret.c - ret.b * ret.e.y) / ret.a; 186 } 187 } 188 else 189 { 190 ret.e.x = 0.0; 191 ret.e.y = - ret.c / ret.b; 192 if(ret.e == ret. s) 193 { 194 ret.e.x = 1e10; 195 ret.e.y = - (ret.c - ret.a * ret.e.x) / ret.b; 196 } 197 } 198 return ret; 199 } 200 201 //------------直線和直線(向量)------------- 202 //向量向左邊平移t的距離 203 Line& moveLine( double t) 204 { 205 Point of; 206 of = Point( -( e.y - s.y), e.x - s.x); 207 double dis = sqrt( of.x * of.x + of.y * of.y); 208 of.x= of.x * t / dis, of.y = of.y * t / dis; 209 s = s + of, e = e + of; 210 return *this; 211 } 212 //直線重合 213 static bool equal(const Line &_st,const Line &_se) 214 { 215 return _st.has( _se.e) && _se.has( _st.s); 216 } 217 //直線平行 218 static bool parallel(const Line &_st,const Line &_se) 219 { 220 return sgn( _st / _se, 0) == 0; 221 } 222 //兩直線(線段)交點 223 //返回-1代表平行,0代表重合,1代表相交 224 static bool crossLPt(const Line &_st,const Line &_se, Point &ret) 225 { 226 if(parallel(_st,_se)) 227 { 228 if(Line::equal(_st,_se)) return 0; 229 return -1; 230 } 231 ret = _st.s; 232 double t = ( Line(_st.s,_se.s) / _se) / ( _st / _se); 233 ret.x += (_st.e.x - _st.s.x) * t; 234 ret.y += (_st.e.y - _st.s.y) * t; 235 return 1; 236 } 237 //------------線段和直線(向量)---------- 238 //直線和線段相交 239 //參數:直線[_st],線段[_se] 240 friend bool crossSL( Line &_st, Line &_se) 241 { 242 return sgn( xmult( _st.s, _se.s, _st.e) * xmult( _st.s, _st.e, _se.e), 0) >= 0; 243 } 244 245 //判斷線段是否相交(註意添加eps) 246 static bool isCrossSS( const Line &_st, const Line &_se) 247 { 248 //1.快速排斥試驗判斷以兩條線段為對角線的兩個矩形是否相交 249 //2.跨立試驗(等於0時端點重合) 250 return 251 max(_st.s.x, _st.e.x) >= min(_se.s.x, _se.e.x) && 252 max(_se.s.x, _se.e.x) >= min(_st.s.x, _st.e.x) && 253 max(_st.s.y, _st.e.y) >= min(_se.s.y, _se.e.y) && 254 max(_se.s.y, _se.e.y) >= min(_st.s.y, _st.e.y) && 255 sgn( xmult( _se.s, _st.s, _se.e) * xmult( _se.s, _se.e, _st.s), 0) >= 0 && 256 sgn( xmult( _st.s, _se.s, _st.e) * xmult( _st.s, _st.e, _se.s), 0) >= 0; 257 } 258 }; 259 260 //尋找凸包的graham 掃描法所需的排序函數 261 Point gsort; 262 bool gcmp( const Point &ta, const Point &tb)/// 選取與最後一條確定邊夾角最小的點,即余弦值最大者 263 { 264 double tmp = xmult( gsort, ta, tb); 265 if( fabs( tmp) < eps) 266 return getdis( gsort, ta) < getdis( gsort, tb); 267 else if( tmp > 0) 268 return 1; 269 return 0; 270 } 271 272 273 274 class triangle 275 { 276 public: 277 Point a, b, c;//頂點 278 triangle(){} 279 triangle(Point a, Point b, Point c): a(a), b(b), c(c){} 280 281 //計算三角形面積 282 double area() 283 { 284 return fabs( xmult(a, b, c)) / 2.0; 285 } 286 287 //計算三角形外心 288 //返回:外接圓圓心 289 Point circumcenter() 290 { 291 double pa = a.x * a.x + a.y * a.y; 292 double pb = b.x * b.x + b.y * b.y; 293 double pc = c.x * c.x + c.y * c.y; 294 double ta = pa * ( b.y - c.y) - pb * ( a.y - c.y) + pc * ( a.y - b.y); 295 double tb = -pa * ( b.x - c.x) + pb * ( a.x - c.x) - pc * ( a.x - b.x); 296 double tc = a.x * ( b.y - c.y) - b.x * ( a.y - c.y) + c.x * ( a.y - b.y); 297 return Point( ta / 2.0 / tc, tb / 2.0 / tc); 298 } 299 300 //計算三角形內心 301 //返回:內接圓圓心 302 Point incenter() 303 { 304 Line u, v; 305 double m, n; 306 u.s = a; 307 m = atan2(b.y - a.y, b.x - a.x); 308 n = atan2(c.y - a.y, c.x - a.x); 309 u.e.x = u.s.x + cos((m + n) / 2); 310 u.e.y = u.s.y + sin((m + n) / 2); 311 v.s = b; 312 m = atan2(a.y - b.y, a.x - b.x); 313 n = atan2(c.y - b.y, c.x - b.x); 314 v.e.x = v.s.x + cos((m + n) / 2); 315 v.e.y = v.s.y + sin((m + n) / 2); 316 Point ret; 317 Line::crossLPt(u,v,ret); 318 return ret; 319 } 320 321 //計算三角形垂心 322 //返回:高的交點 323 Point perpencenter() 324 { 325 Line u,v; 326 u.s = c; 327 u.e.x = u.s.x - a.y + b.y; 328 u.e.y = u.s.y + a.x - b.x; 329 v.s = b; 330 v.e.x = v.s.x - a.y + c.y; 331 v.e.y = v.s.y + a.x - c.x; 332 Point ret; 333 Line::crossLPt(u,v,ret); 334 return ret; 335 } 336 337 //計算三角形重心 338 //返回:重心 339 //到三角形三頂點距離的平方和最小的點 340 //三角形內到三邊距離之積最大的點 341 Point barycenter() 342 { 343 Line u,v; 344 u.s.x = (a.x + b.x) / 2; 345 u.s.y = (a.y + b.y) / 2; 346 u.e = c; 347 v.s.x = (a.x + c.x) / 2; 348 v.s.y = (a.y + c.y) / 2; 349 v.e = b; 350 Point ret; 351 Line::crossLPt(u,v,ret); 352 return ret; 353 } 354 355 //計算三角形費馬點 356 //返回:到三角形三頂點距離之和最小的點 357 Point fermentPoint() 358 { 359 Point u, v; 360 double step = fabs(a.x) + fabs(a.y) + fabs(b.x) + fabs(b.y) + fabs(c.x) + fabs(c.y); 361 int i, j, k; 362 u.x = (a.x + b.x + c.x) / 3; 363 u.y = (a.y + b.y + c.y) / 3; 364 while (step > eps) 365 { 366 for (k = 0; k < 10; step /= 2, k ++) 367 { 368 for (i = -1; i <= 1; i ++) 369 { 370 for (j =- 1; j <= 1; j ++) 371 { 372 v.x = u.x + step * i; 373 v.y = u.y + step * j; 374 if (getdis(u,a) + getdis(u,b) + getdis(u,c) > getdis(v,a) + getdis(v,b) + getdis(v,c)) 375 u = v; 376 } 377 } 378 } 379 } 380 return u; 381 } 382 }; 383 384 triangle tr; 385 int main(void) 386 { 387 int n; 388 scanf("%d",&n); 389 while(n--) 390 { 391 scanf("%lf%lf%lf%lf%lf%lf",&tr.a.x,&tr.a.y,&tr.b.x,&tr.b.y,&tr.c.x,&tr.c.y); 392 Point ans=tr.perpencenter(); 393 printf("%.4f %.4f\n",ans.x,ans.y); 394 } 395 return 0; 396 }
poj1673 EXOCENTER OF A TRIANGLE
