noi2010 ins com turn main www sub tdi ostream

2007: [Noi2010]海拔

Time Limit: 20 Sec Memory Limit: 552 MB
Submit: 2742 Solved: 1318
[Submit][Status][Discuss]

Description

YT市是一個規劃良好的城市，城市被東西向和南北向的主幹道劃分為n×n個區域。簡單起見，可以將YT市看作一個 正方形，每一個區域也可看作一個正方形。從而，YT城市中包括(n+1)×(n+1)個交叉路口和2n×(n+1)條雙向道路 （簡稱道路），每條雙向道路連接主幹道上兩個相鄰的交叉路口。下圖為一張YT市的地圖(n = 2)，城市被劃分為2 ×2個區域，包括3×3個交叉路口和12條雙向道路。 小Z作為該市的市長，他根據統計信息得到了每天上班高峰期 間YT市每條道路兩個方向的人流量，即在高峰期間沿著該方向通過這條道路的人數。每一個交叉路口都有不同的海 拔高度值，YT市市民認為爬坡是一件非常累的事情，每向上爬h的高度，就需要消耗h的體力。如果是下坡的話，則 不需要耗費體力。因此如果一段道路的終點海拔減去起點海拔的值為h(註意h可能是負數)，那麽一個人經過這段路 所消耗的體力是max{0, h}（這裏max{a, b}表示取a, b兩個值中的較大值）。 小Z還測量得到這個城市西北角的交 叉路口海拔為0，東南角的交叉路口海拔為1(如上圖所示)，但其它交叉路口的海拔高度都無法得知。小Z想知道在 最理想的情況下（即你可以任意假設其他路口的海拔高度），每天上班高峰期間所有人爬坡所消耗的總體力和的最 小值。

Input

第一行包含一個整數n，含義如上文所示。接下來4n(n + 1)行，每行包含一個非負整數分別表示每一條道路每一個 方向的人流量信息。輸入順序：n(n + 1)個數表示所有從西到東方向的人流量，然後n(n + 1)個數表示所有從北到 南方向的人流量，n(n + 1)個數表示所有從東到西方向的人流量，最後是n(n + 1)個數表示所有從南到北方向的人 流量。對於每一個方向，輸入順序按照起點由北向南，若南北方向相同時由西到東的順序給出(參見樣例輸入)。

Output

僅包含一個數，表示在最理想情況下每天上班高峰期間所有人爬坡所消耗的總體力和（即總體力和的最小值），結 果四舍五入到整數。

Sample Input

1
1
2
3
4
5
6
7
8

Sample Output

3

【樣例說明】
樣例數據見下圖。


最理想情況下所有點的海拔如上圖所示。
對於100%的數據：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均為整數。
題解：

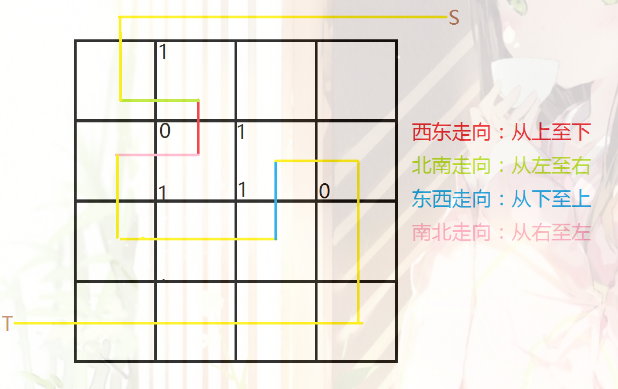
顯然我們只需要考慮0和1的分界線在何處即可。當然我們需要找到一些邊集，把圖分成兩半，且權值和最小。這不就是最小割嗎...所以直接把原圖轉成對偶圖，然後跑dijkstra。

　　註意連邊的時候考慮方向，我們不妨假定對偶圖邊經過的方向，左邊海拔為0，右邊海拔為1，然後只要算0到1的，所以就是正方向的權值。所以我們只需要把方向相反的兩條邊在對偶圖中也構出方向相反的即可。

這樣就可以了。

 1 #include<algorithm>
 2 #include<iostream>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<cmath>
 6 #include<vector>
 7 #include<queue>
 8 #define N 507
 9 using namespace std;
10 
11 int n;
12 int mp[N][N][4];
13 int dis[N][N];
14 
15 struct dist
16 {
17     int x,y,dis;
18     bool operator < (const dist b) const
19     {
20         return dis>b.dis;
21     }
22 };
23 priority_queue<dist>q;
24 int ans=1e9+7;
25 void insert(int x,int y,int d)
26 {
27     if(d<dis[x][y])
28     {
29         dis[x][y]=d;
30         q.push((dist){x,y,d});
31     }
32     if(y==1)ans=min(ans,d+mp[x][y][1]);
33     if(x==n)ans=min(ans,d+mp[x+1][y][0]);
34 }
35 void Dij()
36 {
37     int i,j;
38     for(i=1;i<=n;i++)
39         insert(1,i,mp[1][i][0]);
40     for(j=1;j<=n;j++)
41         insert(j,n,mp[j][n+1][1]);
42     while(!q.empty())
43     {
44         dist now=q.top();q.pop();
45         if(now.dis>dis[now.x][now.y])continue;
46         int x=now.x,y=now.y;
47         if(x>1) insert(x-1,y,now.dis+mp[now.x][now.y][2]);
48         if(y>1) insert(x,y-1,now.dis+mp[now.x][now.y][1]);
49         if(x<n) insert(x+1,y,now.dis+mp[now.x+1][now.y][0]);
50         if(y<n) insert(x,y+1,now.dis+mp[now.x][now.y+1][3]);
51     }
52 }
53 int main()
54 {
55     scanf("%d",&n);
56     for(int i=1;i<=n+1;i++)
57         for(int j=1;j<=n;j++)
58             scanf("%d",&mp[i][j][0]);//從西到東 
59     for(int i=1;i<=n;i++)
60         for(int j=1;j<=n+1;j++)
61             scanf("%d",&mp[i][j][1]);//從北到南 
62     for(int i=1;i<=n+1;i++)
63         for(int j=1;j<=n;j++)
64             scanf("%d",&mp[i][j][2]);//從東到西 
65     for(int i=1;i<=n;i++)
66         for(int j=1;j<=n+1;j++)
67             scanf("%d",&mp[i][j][3]);//從南到北 
68     memset(dis,0x3f,sizeof dis);
69     Dij();
70     cout<<ans<<endl;
71 }

Bzoj2007 [Noi2010]海拔（平面圖最短路）