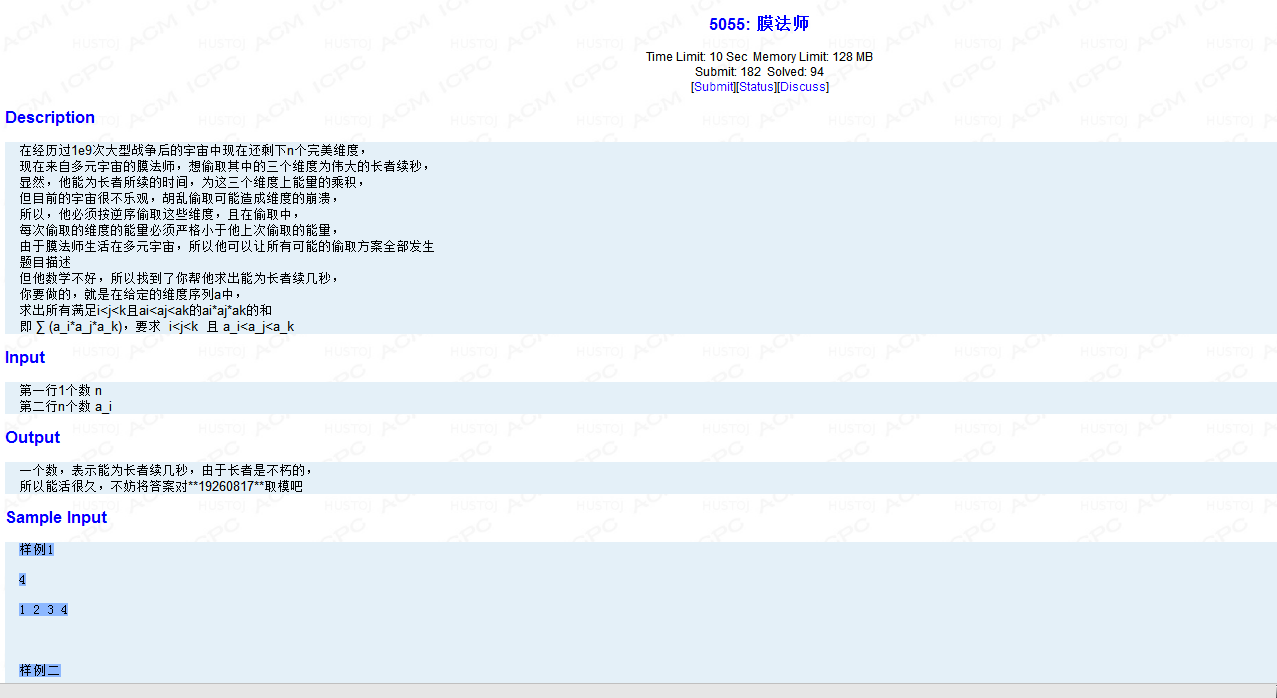
先枚舉每一個數，看它前面有幾個比它小，算一下和為sum1，後面有幾個比它大，算一下和為sum2，對答案的貢獻為A[i]*sum1*sum2。

離散化後，樹狀數組就可以了。

就是倒著一邊，順著一邊，統計就ok了，離散是為了大小，先後順序（方便去重）

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<cmath>
 4 #include<iostream>
 5 #include<cstring>
 6 #include<map>
 7 #define mod 19260817
 8
 
 #define N 300007
 9 #define ll long long
10 using namespace std;
11 
12 int n,top;
13 ll ans;
14 ll a[N],tree[N],c[N];
15 map<int,int>p;
16 struct Node
17 {
18     int zhi,id;
19 }b[N];
20 
21 bool cmp(Node x,Node y)
22 {
23     return x.zhi<y.zhi;
24 }
25 int lowbit(int x){return x&(-x);}
26
 
 ll query(int x)
27 {
28     ll res=0;
29     for (int i=x;i>=1;i-=lowbit(i))
30         res+=tree[i];
31     res%=mod;
32     return res;    
33 }
34 void add(int x,ll z)
35 {
36     for (int i=x;i<=top;i+=lowbit(i))
37         tree[i]=(tree[i]+z)%mod;
38 }
39 int main()
40 {
41     p.clear();
42
 
     scanf("%d",&n);
43     for (int i=1;i<=n;i++)
44     {
45         scanf("%d",&a[i]);
46         a[i]%=mod;
47         b[i].zhi=a[i];
48         b[i].id=i;
49     }
50     sort(b+1,b+n+1,cmp);
51     b[0].zhi=-1000;
52     for (int i=1;i<=n;i++)
53         if (b[i].zhi!=b[i-1].zhi) p[b[i].zhi]=++top;
54     for (int i=1;i<=n;i++)
55     {
56         c[i]=1ll*query(p[a[i]]-1)*a[i]%mod;
57         add(p[a[i]],a[i]);
58     }
59     memset(tree,0,sizeof(tree));
60     for (int i=n;i>=1;i--)
61     {
62         ans=(ans+1ll*c[i]*(query(top)-query(p[a[i]])+mod))%mod;
63         add(p[a[i]],a[i]);
64     }
65     printf("%lld",ans);
66 }

bzoj 5055: 膜法師 樹狀數組+離散