ACM-ICPC (10/12)
阿新 • • 發佈：2017-10-12
mat space max 貪心 起點 from oid ade stdin
01分數規劃
背景：根據樓教主回憶，曾經在一場比賽中秒掉了一道最優比例生成樹問題，導致很多人跟風失敗，最終悲劇。
-
什麽是01分數規劃呢？
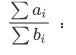這樣的等式求最大，最小即為01分數規劃。
如果你不知道該如何去解，你可能會去貪心，DP去做，但是這樣是很復雜的。
-
解法：二分，叠代（計算幾何大佬都知道這種方案，但是我不是）
-
直接二分ans，? ? ? 根據符號二分轉移。
例題一：pku 2796
題意：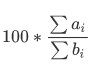 
最大。
#include <stdio.h> #include <algorithm> ?using namespace std; ? const int maxn = 1005; ? int n,k; double a[maxn],b[maxn]; double c[maxn]; ? bool cmp(double a,double b) { return a > b; } ? bool calc(double x) { for(int i = 0; i < n; i++) c[i] = a[i] - x*b[i]; sort(c,c+n,cmp); ? double sum = 0;for(int i = 0; i < n-k; i++) sum +=c[i]; if(sum>=0) return true; return false; ? } ? int main() { //freopen("in.txt","r",stdin); while(scanf("%d%d",&n,&k),n) { ? for(int i = 0; i < n; i++) scanf("%lf",&a[i]); for(int i = 0; i < n; i++) scanf("%lf",&b[i]); ? double l = 0,r = 1; ? while(r-l>1e-6) { double mid = (l + r)/2; ? if(calc(mid)) l = mid; else r = mid; ? } printf("%.0lf\n",l*100); ? } return 0; }
例題二：pku 2728 最優比例生成樹
題意：給定n 個點，坐標(x,y,z)，n條無向邊的圖，國王將這n個點連起來（生成樹），建一條邊有花費， 求單位最小花費最小比例。
同理：二分這個比例，邊權為 ，最小生成樹 ans >= 0，說明 x過小，二分轉移 l = mid；
#include <stdio.h> #include <string.h> #include <math.h> #include <vector> #include <queue> #include <map> #include <set> #include <iostream> #include <algorithm> ? using namespace std; ? const int maxn = 1005; ? double maps[maxn][maxn]; bool vis[maxn]; double dis[maxn]; ? int n; ? double Prim() { memset(vis,false,sizeof(vis)); for(int i = 1; i<= n; i++) dis[i] = 1000000000; ? double ans = 0; dis[1] = 0; ? for(int i = 1; i <= n; i++) { double tmp = 1000000000; int k = 0; ? for(int j = 1; j <= n; j++) { if(!vis[j]&&dis[j]<tmp) { tmp = dis[j]; k = j; } } ? vis[k] = true; ans += tmp; ? for(int j = 1; j<= n; j++) { if(!vis[j]&&dis[j]>maps[k][j]) dis[j] = maps[k][j]; } ? } return ans; } ? struct Node { double x,y,z; }nodes[maxn]; ? double dist(int i,int j,double x) { double fx = fabs(nodes[i].x-nodes[j].x); double fy = fabs(nodes[i].y-nodes[j].y); double fz = fabs(nodes[i].z-nodes[j].z); return fz - x*sqrt(fx*fx+fy*fy); } ? double eps = 1e-4; ? int main() { //freopen("in.txt","r",stdin); while(scanf("%d",&n),n) { ? for(int i = 1; i <= n; i++) scanf("%lf%lf%lf",&nodes[i].x,&nodes[i].y,&nodes[i].z); ? double l = 0,r = 1000000000; ? while(r-l>1e-5) { double mid = (r+l)/2; ? for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) maps[i][j] = dist(i,j,mid); ? double ans = Prim(); ? if(ans<=0) r = mid; else l = mid; } ? printf("%.3f\n",l); } ? return 0; }
例題三：pku 3621 最優比例環。（雙倍經驗題Uva 11090，題意相反）
題意：給定一個L個節點，P條有向邊的圖，奶牛從一個城市出發，走一個環回到起點，點上有權值，邊上也有長度，求單位長度的點權最大。
分析：還是二分 ans，由於是一個環，一條邊上，算起點權值就好了。改邊權， ，
由於求的是比例最大，這時SPFA，應反向松弛，才能得到最大的比例。
#include <stdio.h> #include <string.h> #include <math.h> #include <string.h> #include <vector> #include <set> #include <map> #include <queue> #include <string> #include <iostream> #include <algorithm> ? using namespace std; ? const int maxn = 1005; ? struct Edge { int from,to; double dist; }; ? struct BellmanFord { int n, m; vector<Edge> edges; vector<int> G[maxn]; bool inq[maxn]; double d[maxn]; int p[maxn]; int cnt[maxn]; ? void init(int n) { this->n = n; for(int i = 0; i < n; i++) G[i].clear(); edges.clear(); } ? void AddEdge(int from, int to, double dist) { edges.push_back((Edge) { from, to, dist }); m = edges.size(); G[from].push_back(m-1); } ? bool negativeCycle() { queue<int> Q; memset(inq, 0, sizeof(inq)); memset(cnt, 0, sizeof(cnt)); for(int i = 0; i < n; i++) { d[i] = 0; inq[0] = true; Q.push(i); } ? while(!Q.empty()) { int u = Q.front(); Q.pop(); inq[u] = false; for(int i = 0; i < (int)G[u].size(); i++) { Edge& e = edges[G[u][i]]; if(d[e.to] < d[u] + e.dist) //反向松弛 { d[e.to] = d[u] + e.dist; p[e.to] = G[u][i]; if(!inq[e.to]) { Q.push(e.to); inq[e.to] = true; if(++cnt[e.to] > n) return true; } } } } return false; } }sol; int L,P; double f[maxn]; double t[maxn]; ? vector<Edge> edgestmp; ? int main() { //freopen("in.txt","r",stdin); scanf("%d%d",&L,&P); ? sol.init(L); for(int i = 0; i < L; i++) scanf("%lf",&f[i]); for(int i = 0; i < P; i++) { int u,v; double dist; scanf("%d%d%lf",&u,&v,&dist); u--;v--; edgestmp.push_back((Edge){u,v,dist}); sol.AddEdge(u,v,dist); } ? double l = 0,r = 10000; while(r-l>1e-4) { double mid = (r+l)/2; ? sol.init(L); ? for(int i = 0; i < P; i++) { int u = edgestmp[i].from; int v = edgestmp[i].to; double dist = edgestmp[i].dist; sol.AddEdge(u,v,f[u]-mid*dist); } ? if(sol.negativeCycle()) l = mid; else r = mid; } ? printf("%.2f\n",l); return 0; }
ACM-ICPC (10/12)