題目背景

棧是計算機中經典的數據結構，簡單的說，棧就是限制在一端進行插入刪除操作的線性表。

棧有兩種最重要的操作，即pop（從棧頂彈出一個元素）和push（將一個元素進棧）。

棧的重要性不言自明，任何一門數據結構的課程都會介紹棧。寧寧同學在復習棧的基本概念時，想到了一個書上沒有講過的問題，而他自己無法給出答案，所以需要你的幫忙。

題目描述

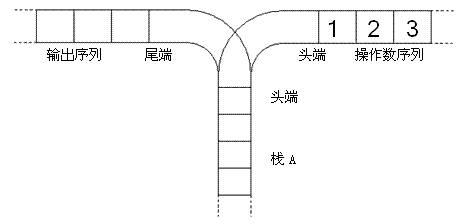
寧寧考慮的是這樣一個問題：一個操作數序列，從1，2，一直到n（圖示為1到3的情況），棧A的深度大於n。

現在可以進行兩種操作，

1.將一個數，從操作數序列的頭端移到棧的頭端（對應數據結構棧的push操作）

2. 將一個數，從棧的頭端移到輸出序列的尾端（對應數據結構棧的pop操作）

使用這兩種操作，由一個操作數序列就可以得到一系列的輸出序列，下圖所示為由1 2 3生成序列2 3 1的過程。

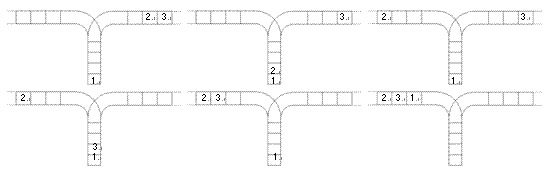
（原始狀態如上圖所示）

你的程序將對給定的n，計算並輸出由操作數序列1，2，…，n經過操作可能得到的輸出序列的總數。

輸入輸出格式

輸入格式：

輸入文件只含一個整數n（1≤n≤18）

輸出格式：

輸出文件只有一行，即可能輸出序列的總數目

輸入輸出樣例

3

5

題解：卡特蘭數經典應用。
假設k是最後一個出棧的，那麽1--k-1一定比k先出棧，就是f[k-1]，
那麽n-k+1--n就是f[k+1]，相乘就行了。
代碼：

#include<cstdio>
using
 
 namespace std;
int h[110];
int main()
{
    int n,i,j;
    h[0]=1;
    scanf("%d",&n);
    for(i=1;i<=n;++i)
        for(j=0;j<i;++j)
            h[i]=(h[i]+h[j]*h[i-1-j]);
    printf("%d\n",h[n]);
    return 0;
}

洛谷 P1044 棧