信息熵，交叉熵，KL散度
0 前言
上課的時候老師講到了信息論中的一些概念，看到交叉熵，這個概念經常用在機器學習中的損失函數中。
這部分知識算是機器學習的先備知識，所以查資料加深一下理解。
Reference:
信息熵是什麽，韓迪的回答：https://www.zhihu.com/question/22178202
如何通俗的解釋交叉熵於相對熵，匿名用戶的回答和張一山的回答：https://www.zhihu.com/question/41252833
1 信息熵的抽象定義
熵的概念最早由統計熱力學引入。
信息熵是由信息論之父香農提出來的，它用於隨機變量的不確定性度量，先上信息熵的公式。
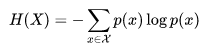
信息是用來減少隨機不確定性的東西（即不確定性的減少）。
我們可以用log ( 1/P )來衡量不確定性。P是一件事情發生的概率，概率越大，不確定性越小。
可以看到信息熵的公式，其實就是log ( 1/P )的期望，就是不確定性的期望，它代表了一個系統的不確定性，信息熵越大，不確定性越大。
註意這個公式有個默認前提，就是X分布下的隨機變量x彼此之間相互獨立。還有log的底默認為2，實際上底是多少都可以，但是在信息論中我們經常討論的是二進制和比特，所以用2。
信息熵在聯合概率分布的自然推廣，就得到了聯合熵
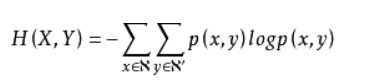
當X, Y相互獨立時，H(X, Y) = H(X) + H(Y)
當X和Y不獨立時，可以用 I(X, Y) = H(X) + H(Y) - H(X, Y) 衡量兩個分布的相關性，這個定義比較少用到。
2 信息熵的實例解釋
舉個例子說明信息熵的作用。
例子是知乎上看來的，我覺得講的挺好的。
比如賭馬比賽，有4匹馬{ A, B, C, D}，獲勝概率分別為{ 1/2, 1/4, 1/8, 1/8 }，將哪一匹馬獲勝視為隨機變量X屬於 { A, B, C, D } 。
假定我們需要用盡可能少的二元問題來確定隨機變量 X 的取值。
例如，問題1：A獲勝了嗎？ 問題2：B獲勝了嗎？ 問題3：C獲勝了嗎？
最後我們可以通過最多3個二元問題，來確定取值。
如果X = A，那麽需要問1次（問題1：是不是A？），概率為1/2
如果X = B，那麽需要問2次（問題1：是不是A？問題2：是不是B？），概率為1/4
如果X = C，那麽需要問3次（問題1，問題2，問題3），概率為1/8
如果X = D，那麽需要問3次（問題1，問題2，問題3），概率為1/8
那麽為確定X取值的二元問題的數量為
回到信息熵的定義，會發現通過之前的信息熵公式，神奇地得到了：
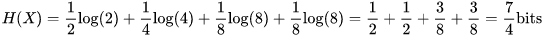
在二進制計算機中，一個比特為0或1，其實就代表了一個二元問題的回答。也就是說，在計算機中，我們給哪一匹馬奪冠這個事件進行編碼，所需要的平均碼長為1.75個比特。
很顯然，為了盡可能減少碼長，我們要給發生概率
較大的事件，分配較短的碼長
。這個問題深入討論，可以得出霍夫曼編碼的概念。
霍夫曼編碼就是利用了這種大概率事件分配短碼的思想，而且可以證明這種編碼方式是最優的。我們可以證明上述現象：
- 為了獲得信息熵為
的隨機變量
的一個樣本，平均需要拋擲均勻硬幣（或二元問題）
- 信息熵是數據壓縮的一個臨界值（參考碼長部分的案例）
所以，信息熵H(X)可以看做，對X中的樣本進行編碼所需要的編碼長度的期望值。它代表了編碼方案
3 交叉熵和KL散度
上一節說了信息熵H(X)可以看做，對X中的樣本進行編碼所需要的編碼長度的期望值。
這裏可以引申出交叉熵的理解，現在有兩個分布，真實分布p和非真實分布q，我們的樣本來自真實分布p。
按照真實分布p來編碼樣本所需的編碼長度的期望為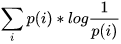
，這就是上面說的信息熵H( p )
按照不真實分布q來編碼樣本所需的編碼長度的期望為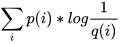
，這就是所謂的交叉熵H( p,q )
這裏引申出KL散度D(p||q) = H(p,q) - H(p) =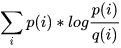 
，也叫做相對熵，它表示兩個分布的差異，差異越大，相對熵越大。
機器學習中，我們用非真實分布q去預測真實分布p，因為真實分布p是固定的，D(p||q) = H(p,q) - H(p) 中 H(p) 固定，也就是說交叉熵H(p,q)越大，相對熵D(p||q)越大，兩個分布的差異越大。
所以交叉熵用來做損失函數就是這個道理，它衡量了真實分布和預測分布的差異性。
信息熵，交叉熵，KL散度