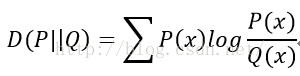Kullback–Leibler divergence(相對熵,KL距離,KL散度)
阿新 • • 發佈:2019-02-05
1 前言
注意兩個名詞的區別:
相對熵:Kullback–Leibler divergence
交叉熵:cross entropy
KL距離的幾個用途:
① 衡量兩個概率分佈的差異。
② 衡量利用概率分佈Q 擬合概率分佈P 時的能量損耗,也就是說擬合以後丟失了多少的資訊,可以參考前面曲線擬合的思想。
③ 對①的另一種說法,就是衡量兩個概率分佈的相似度,在運動捕捉裡面可以衡量未新增標籤的運動與已新增標籤的運動,進而進行運動的分類。
百度百科解釋的為什麼KL距離不準確,不滿足距離的概念:
①KL散度不對稱,即P到Q的距離,不等於Q到P的距離
②KL散度不滿足三角距離公式,兩邊之和大於第三邊,兩邊之差小於第三邊。
2. 相對熵數學定義
KL散度的值始終大於0,並且當且僅當兩分佈相同時,KL散度等於0.
從另一個角度也就可以發現,當P(x)和Q(x) 的相似度越高,KL距離越小。
有一個例項,可以參考:http://www.cnblogs.com/finallyliuyu/archive/2010/03/12/1684015.html
3. 交叉熵和相對熵
作者:do Cre連結:https://www.zhihu.com/question/41252833/answer/108777563
來源:知乎
熵的本質是夏農資訊量
 的期望。
的期望。現有關於樣本集的2個概率分佈p和q,其中p為真實分佈,q非真實分佈。按照真實分佈p來衡量識別一個樣本的所需要的編碼長度的期望(即平均編碼長度)為:

如果使用錯誤分佈q來表示來自真實分佈p的平均編碼長度,則應該是:
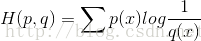
因為用q來編碼的樣本來自分佈p,所以期望H(p,q)中概率是p(i)。H(p,q)我們稱之為“交叉熵”。
比如含有4個字母(A,B,C,D)的資料集中,真實分佈p=(1/2, 1/2, 0, 0),即A和B出現的概率均為1/2,C和D出現的概率都為0。計算H(p)為1,即只需要1位編碼即可識別A和B。如果使用分佈Q=(1/4, 1/4, 1/4, 1/4)來編碼則得到H(p,q)=2,即需要2位編碼來識別A和B(當然還有C和D,儘管C和D並不會出現,因為真實分佈p中C和D出現的概率為0,這裡就欽定概率為0的事件不會發生啦)。
可以看到上例中根據非真實分佈q得到的平均編碼長度H(p,q)大於根據真實分佈p得到的平均編碼長度H(p)。事實上,根據

其又被稱為KL散度(Kullback–Leibler divergence,KLD)Kullback–Leibler divergence。它表示2個函式或概率分佈的差異性:差異越大則相對熵越大,差異越小則相對熵越小,特別地,若2者相同則熵為0。注意,KL散度的非對稱性。
比如TD-IDF演算法就可以理解為相對熵的應用:詞頻在整個語料庫的分佈與詞頻在具體文件中分佈之間的差異性。
交叉熵可在神經網路(機器學習)中作為損失函式,p表示真實標記的分佈,q則為訓練後的模型的預測標記分佈,交叉熵損失函式可以衡量p與q的相似性。交叉熵作為損失函式還有一個好處是使用sigmoid函式在梯度下降時能避免均方誤差損失函式學習速率降低的問題,因為學習速率可以被輸出的誤差所控制。
PS:通常“相對熵”也可稱為“交叉熵”,雖然公式上看相對熵=交叉熵-資訊熵,但由於真實分佈p是固定的,D(p||q)由H(p,q)決定。當然也有特殊情況,彼時2者須區別對待。
稍微說一下中間那個例子,如果真正去計算的話,會發現H(p)=log2,而H(p,q)=log4,然後由於編碼位數必須為整數,所以是向上取整,即得到原作者的答案。
4. 交叉熵損失函式
看到交叉熵,想到機器學習中剛好有“交叉熵損失函式”這個東東,好像是針對二分類的情況,可以將前面的交叉熵公式改成二分類的情況: 交叉熵中用q擬合p,其中的q相當於預測值,p相當於正確的標籤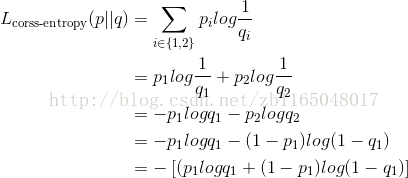
如果想好看點,那麼一般的寫法就是,把y當做正確標籤,o當做網路輸出,那麼
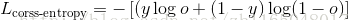
這樣就跟我們經常看到的交叉熵損失函式一模一樣了。