在本系列的第三篇博客中，筆者討論對偶單純形法的相關理論和應用

2.3 Dual Simplex Method(對偶單純形法)

Contents

　　2.3.1 對偶問題產生的原因

　　2.3.2 對偶問題的構造

　　2.3.3 對偶問題的相關定理

　　2.3.4 對偶問題的應用

2.3.1 對偶問題產生原因

在本系列的（二）中我們利用大M法和兩階段法解決一些不符合普通單純形法標準形式的線性規劃問題，不過大M法和兩階段法的使用步驟比較繁瑣

下面考慮兩個問題模型：

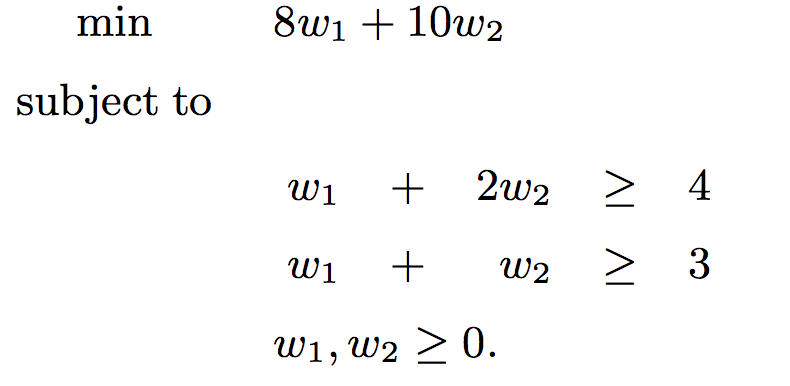
兩個問題之間聯系如下：

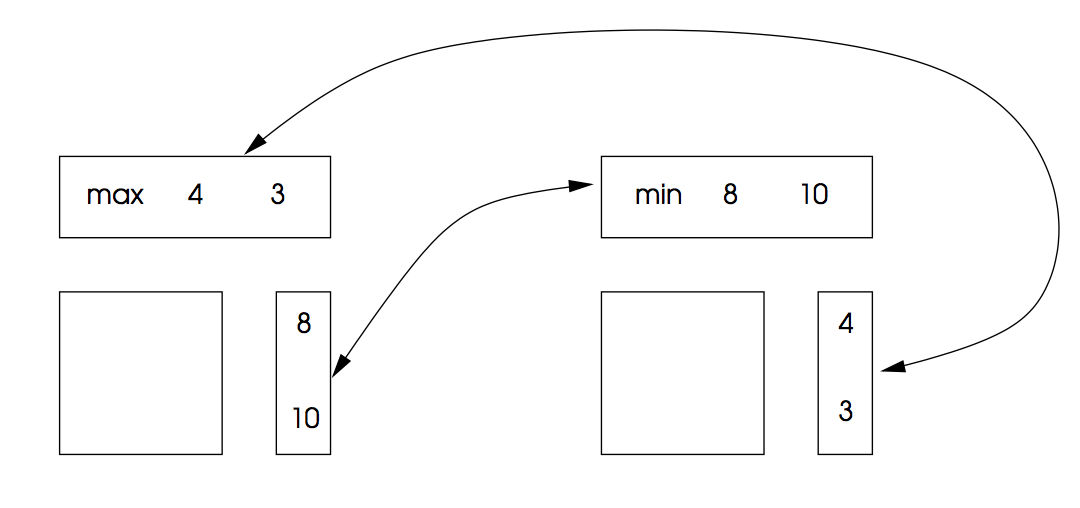
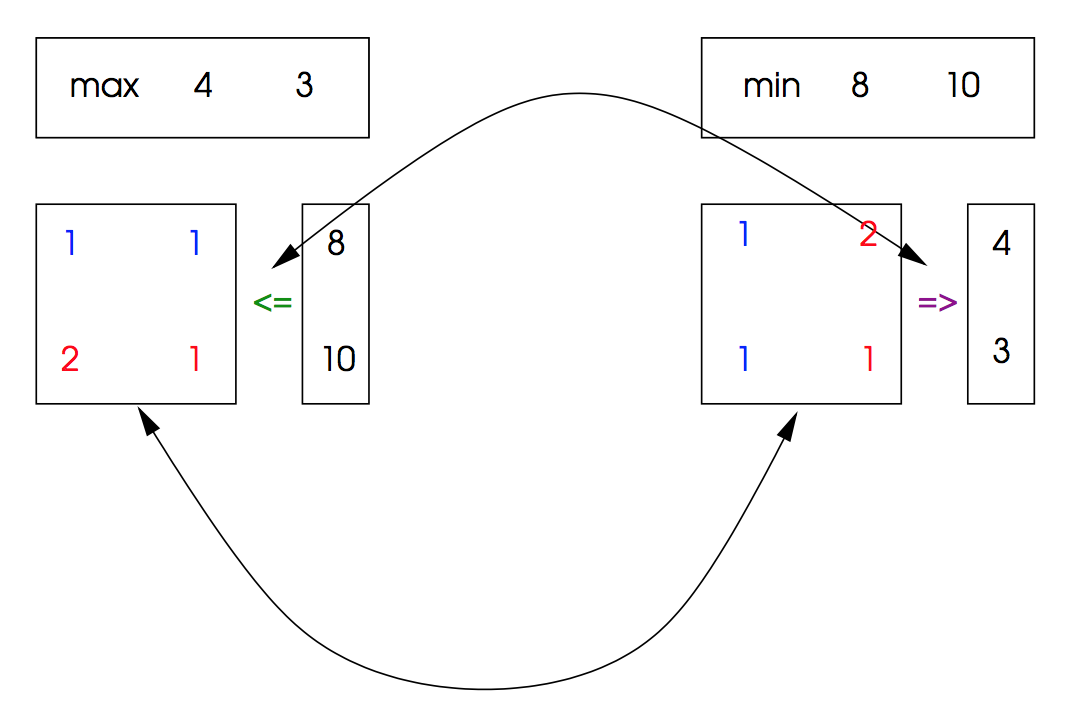
兩個問題的解如下：

目標函數的目標值都是26

這裏放出第一個問題最後的叠代結果：

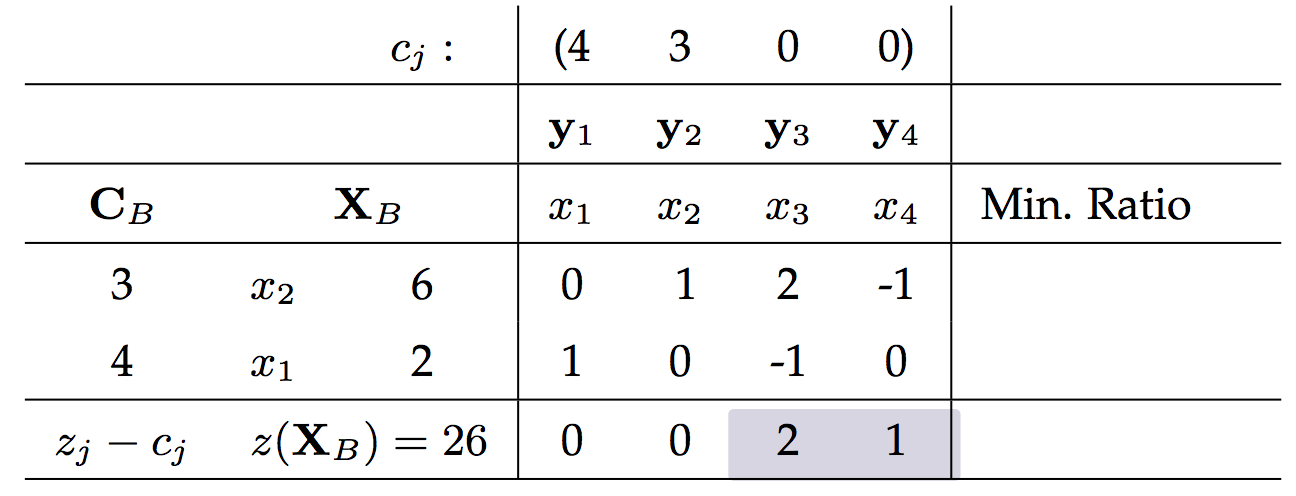
看到陰影部分的值正好是第二個問題的最優解，這裏並不是巧合！！！

對偶性理論指出如果一個線性規劃問題存在最優解，那麽它的對偶問題也存在最優解，並且兩者的結果一致！！

可以這樣理解：類似於生產問題中的最大化收入的問題，等價於租用設備使得成本最小。

2.3.2 構造

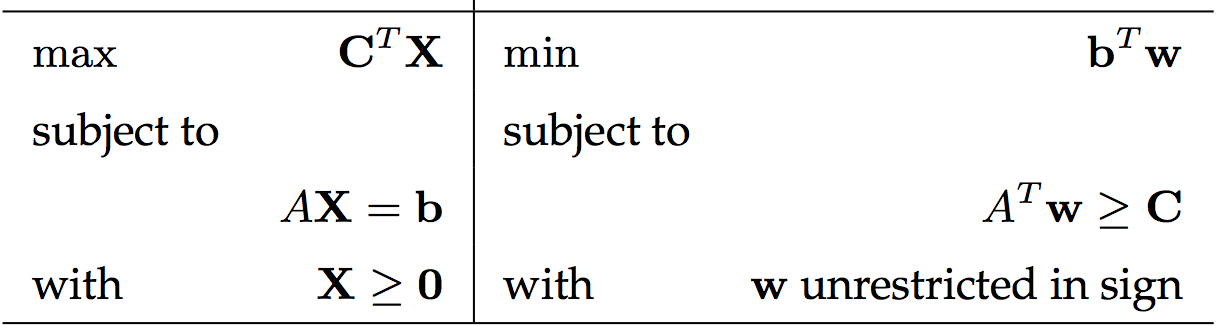
等式約束對應的對偶未知數沒有非負限制

轉化總結如下：

腦容量足夠的朋友可以記一下這個：

不過，可以這樣記住：

1.原問題轉為最大化（最小化），約束符號全是≤（≥），註意這裏的右端值沒有非負限制！！！如此對偶未知數都是非負。

2.對於等式約束，對偶未知數沒有非負限制

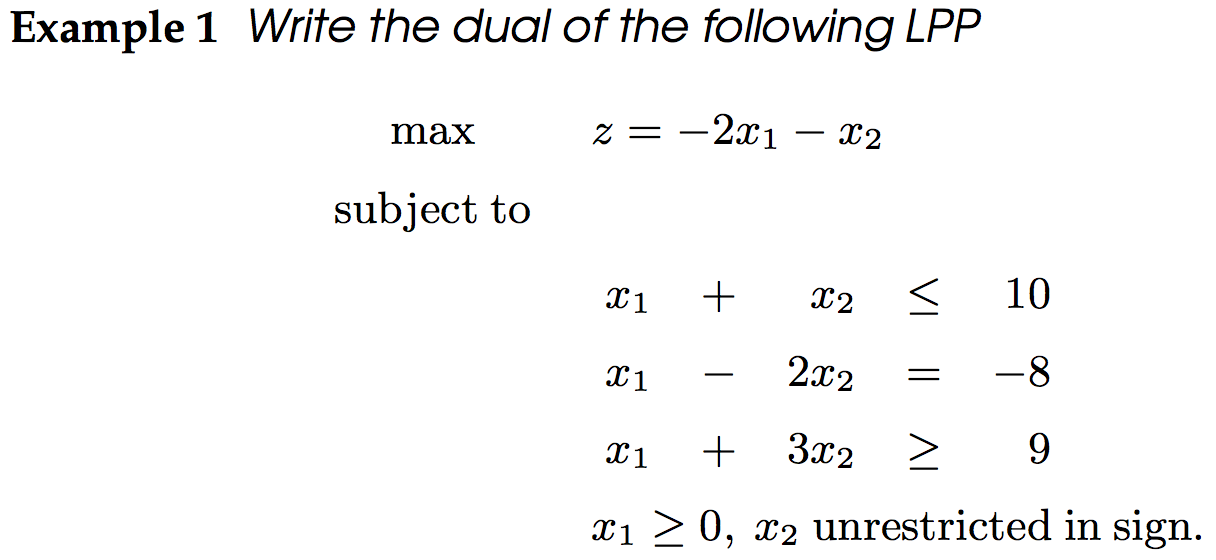
對偶格式為

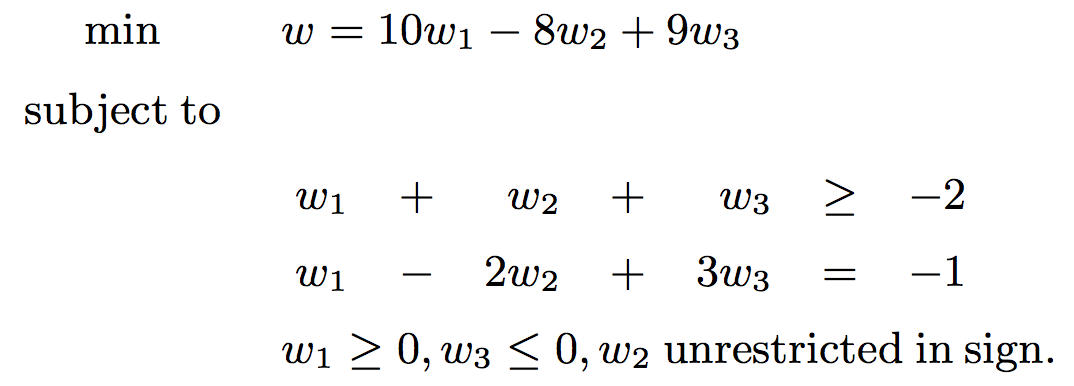
2.3.3 相關定理（原理）

弱對偶定理：

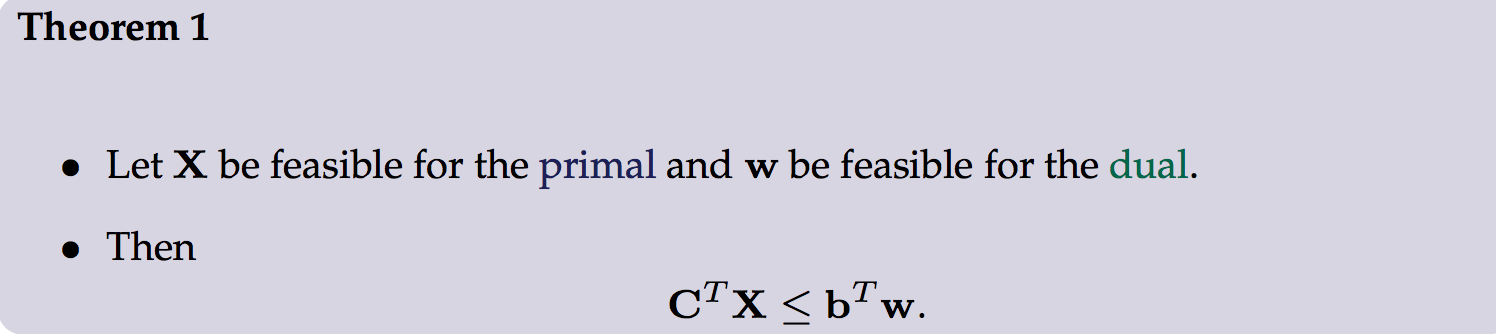
證明如下：

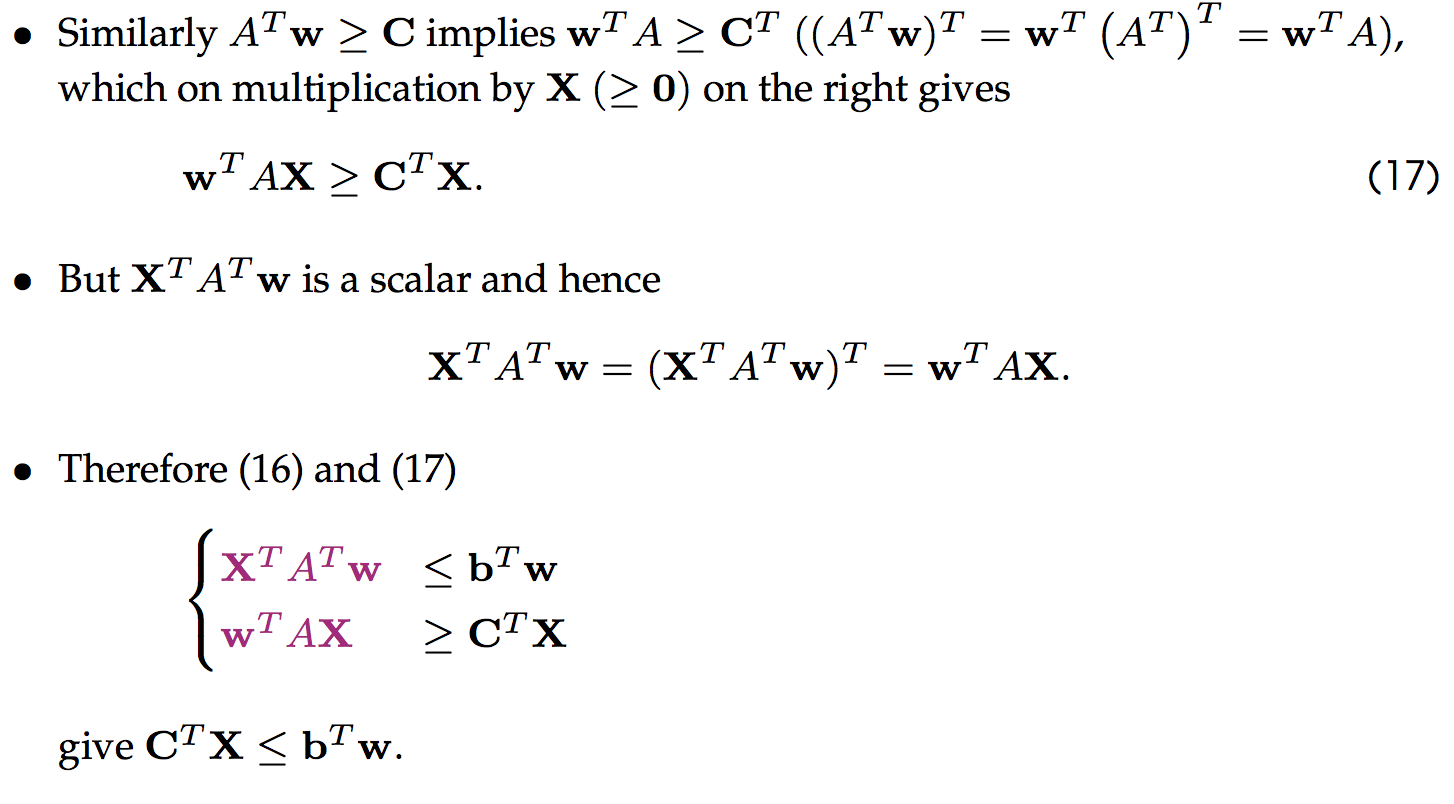
推論

證明：

強對偶定理：

以下是證明，核心思想是：在求出原問題最優解的時候，我們實際上也在求解對偶問題！！

得證

2.3.4 應用

先用matlab解出：

linprog():

f = [2 1];
A = [-4 -3; 1 2];
b = [-6 3];
Aeq = [3 1];
beq = [3];
lb = [0 0];
[x, fval] = linprog(f, A, b, Aeq, beq, lb)

運行結果：

revised():

c = [-2 -1];
A = [3 1; 4 3; 1 2];
b = [3 6 3];
inq = [0 1 -1];
revised(c, b, A, inq, 0)

運行結果：

現在轉化為對偶問題來解答：

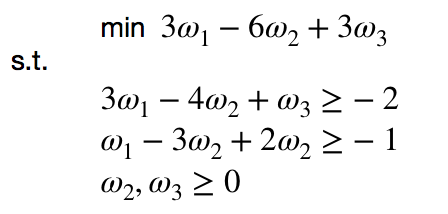
linprog()求解

f = [3 -6 3];
A = [-3 4 -1; -1 3 -2];
b = [2 1];
lb = [-inf, 0 0];
[x, fval] = linprog(f, A, b, [], [], lb)

運行結果：

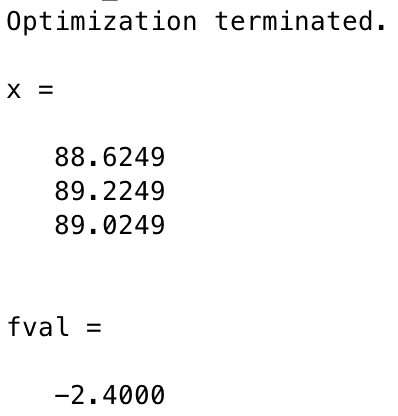
可以看到，目標方程的最優值是一樣的

線性規劃中的單純形法與內點法（原理、步驟以及matlab實現）（三）