雨流計數法的matlab實現,採用三點法與四點法
介紹
雨流計數法是20世紀50年代由英國的兩位工程師M.Matsuishi和T.Endo提出來的。該計數法的主要功能是把實測載荷歷程簡化為若干個載荷迴圈,供疲勞壽命估算和編制疲勞試驗載荷譜使用。它以雙引數法為基礎,考慮了動強度(幅值)和靜強度(均值)兩個變數,符合疲勞載荷本身固有的特性。雨流計數法主要用於工程界,特別在疲勞壽命計算中運用非常廣泛
計數規則
(1)雨流依次從載荷時間歷程的峰值位置的內側沿著斜坡往下流;(2)雨流從某一個峰值點開始流動,當遇到比其起始峰值更大的峰值時要停止流動;(3)雨流遇到上面流下的雨流時,必須停止流動;(4)取出所有的全迴圈,記下每個迴圈的幅度;(5)將第一階段計數後剩下的發散收斂載荷時間歷程等效為一個收斂發散型的載荷時間歷程,進行第二階段的雨流計數。計數迴圈的總數等於兩個計數階段的計數迴圈之和。
計算舉例
在圖1中,雨流法從1點開始,該點認為是最小值。雨流流至2點,豎直下滴到3與4點幅值間的2ˊ點,然後流到4點,最後停於比1點更負的峰值5的對應處。得出一個從1到4的半迴圈。下一個雨流從峰值2點開始,流經3點,停於4點的對面,因為4點是比開始的2點具有更正的最大值,得出一個半迴圈2-3。第三個流動從3點開始,因為遇到由2點滴下的雨流,所以終止於2ˊ點,得出半迴圈3-2ˊ。這樣,3-2和2-3就形成了一個閉合的應力-應變回路環,它們配成一個完全的迴圈2′-3-2。
- 下一個雨流從峰值4開始,流經5點,豎直下滴到6和7之間的5ˊ點,繼續往下流,再從7點豎直下滴到峰值10的對面,因為10點比4點具有更正的最大值。得出半迴圈4-5-7。
- 第五個流動從5點開始,流到6點,豎直下滴,終止於7點的對面,因為7點比5點具有更負的極小值。取出半迴圈5-6。第六個流動從6點開始,因為遇到由5點滴下的雨滴,所以流到5ˊ點終止。半迴圈6-5與5-6配成一個完全迴圈5ˊ-6-5,取出5ˊ-6-5。
- 第七個流動從7點開始,經過8點,下落到9-10線上的8ˊ點,然後到最後的峰值10,取出半迴圈7-8-10。第八個流動從8點開始,流至9點下降到10點的對面終止,因為10點比8點具有更正的最大值。取出半迴圈8-9。最後一個流動從9點開始,因為遇到由8點下滴的雨流,所以終止於8ˊ點。取出半迴圈9-8ˊ。把兩個半迴圈8-9和9-8ˊ配對,組成一個完全的迴圈8-9-8ˊ。
- 這樣,圖1所示的應變一時間記錄包括三個完全迴圈8-9-8ˊ,2-3-2ˊ,5-6-5ˊ和三個半迴圈1-2-4,4-5-7,7-8-10。圖1表明,雨流法得到的應變是與材料應力-應變特性相一致的。從圖1中看出,有三個完全的迴圈,與此對應,在圖2中有三個陰影線所示的閉合迴路。


matlab的三點法實現
clear;clc
C=xlsread('load_F');%%%%%%%%%在此修改載入的檔名,資料格式一直才可正確運算%%%
B=C;A=C;
q=length(A);
%三點迴圈計數法;部分參考SAE ASTM標準
%% 步驟一 %%
%對載荷時間歷程進行處理使它只包含峰谷峰谷交替出現
m=q;
for i=2:1:m-1
if A(i-1)<A(i)&&A(i)<A(i+1)
B(i)=NaN;
elseif A(i-1)>A(i)&&A(i)>A(i+1)
B(i)=NaN;
end
end
B(isnan(B))=[];
%% 步驟二 %%
%對載荷時間歷程再造,使從最大(小)值拆開,前後拼接,使從最值開始最值結束
[a,b]=max(B);
n=length(B);
B1=B(b:n);
B2=B(1:b);
B=[B1;B2];
%% 步驟三 %%
%再只留波峰波谷,防止拼接處出現不合理的資料
A=B;m=length(B);
for i=2:1:m-1
if A(i-1)<A(i)&&A(i)<A(i+1)
B(i)=NaN;
elseif A(i-1)>A(i)&&A(i)>A(i+1)
B(i)=NaN;
end
end
B(isnan(B))=[];n=length(B);
%%%%%%%%%%%%%%%%%%%%%%%% B為改造後載荷時間歷程 n為B中波峰波谷的個數
%% 步驟四 %%
%雨流計數記因素 1幅值F 2均值J 開啟無腦迴圈模式
F=[];J=[];D=B;
while length(B)>=1
n=length(B);
if n==1
break
elseif n>1
for j=1:n-2
s1=abs(B(j+1)-B(j));
s2=abs(B(j+1)-B(j+2));
e3=(B(j)+B(j+1))/2;
if s1<=s2
F=[F;s1];
J=[J;e3];
B(j)=[];
B(j)=[];
n=length(B);
break;
else
continue;
end
end
end
continue
end
%% 步驟五 %%
%畫影象 三維hist三維影象
X=[J,F];
figure;hist3(X,[30 30]);
xlabel('均值');
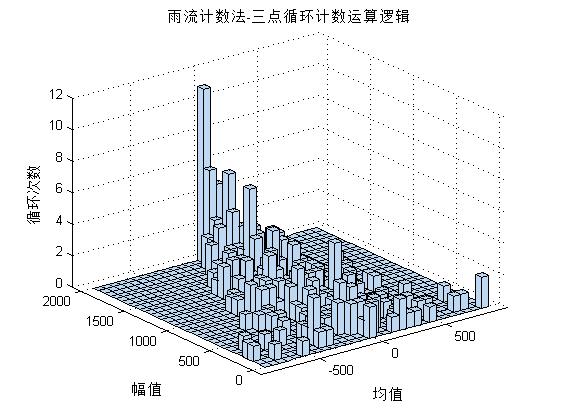
title('雨流計數法-三點迴圈計數運算邏輯');
ylabel('幅值');
zlabel('迴圈次數');
%% 檢驗說明 %%
% load_Ftest運算與手算一致,與其他語言的計算結果幅值F,均值J一直,其他的資料也證明是可以正確執行的
%%%%存在的問題
%拼接後可能會損失拼接處資料,未知是否會對結果有偏差
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 版權所有 轉載請註明原出處網址%
出來的結果圖,參考
四點法的實現
clear;clc
C=xlsread('load_F1');%%%%%%%%%在此修改載入的檔名,資料格式一直才可正確運算%%%
B=C;A=C;
q=length(A);
%四點迴圈計數法
%% 步驟一 %%
%對載荷時間歷程進行處理使它只包含峰谷峰谷交替出現
m=q;
for i=2:1:m-1
if A(i-1)<A(i)&&A(i)<A(i+1)
B(i)=NaN;
elseif A(i-1)>A(i)&&A(i)>A(i+1)
B(i)=NaN;
end
end
B(isnan(B))=[];n=length(B);
%% 步驟二 %%
F=[];J=[];D=B;
while fun(B)==1||fun(B)==0
if fun(B)==1
for j=1:n-4
s1=abs(B(j+1)-B(j+2));
s0=abs(B(j+3)-B(j));
e3=(B(j+2)+B(j+1))/2;
if s1<=s0
F=[F;s1];
J=[J;e3];
B(j+1)=[];
B(j+1)=[];
n=length(B);
break
else
continue
end
end
elseif fun(B)==0
break
end
continue
end
%% 步驟三 %%
%畫影象 三維hist三維影象
X=[J,F];
figure;hist3(X,[30 30]);
xlabel('均值');
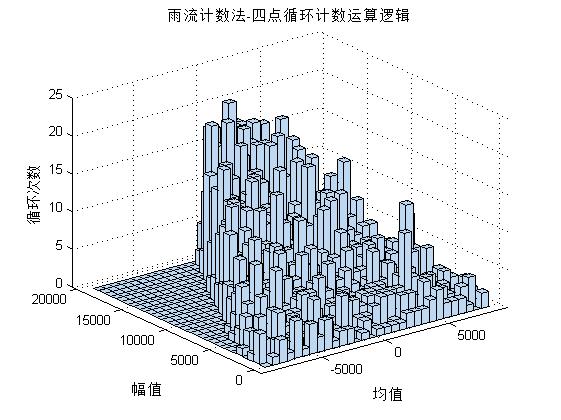
title('雨流計數法-四點迴圈計數運算邏輯');
ylabel('幅值');
zlabel('迴圈次數');出來的結果圖
其中應用的fun函式程式碼
function re=fun(B)
n=length(B);re=0;
for j=1:n-4
s1=abs(B(j+1)-B(j+2));
s0=abs(B(j+3)-B(j));
if s1<=s0
re=1;
break
else
re=0;
continue
end
end
return 以上就是所有的程式碼,下面提供原始檔的下載地址,包括三個函式,一些測試用的資料,一份word版的手算結果與兩者計算結果的簡單情況下的對比。下載網址為https://download.csdn.net/download/u011391128/10286545,或者可以在我本人的上傳檔案中去找。要2個c幣,我也不知道這是什麼東西,選不了0就選的2。
希望能和各位業內人士交流一下如何改進,如果有人能加個gui的介面,萬分感謝,我對gui不太熟,但你要把我的出處註上啊 。最後,如果你是龍凱老師的學生,代我向他問好,順便此題從此以後將不再成為題目。
。最後,如果你是龍凱老師的學生,代我向他問好,順便此題從此以後將不再成為題目。