在Python 中使用 Matplotlib 註釋繪制決策樹形圖

上次我們對數據生成決策樹有了一定了解，但樹是以字典的形式表達的，非常不易於理解；因此，通過決策樹的圖形可視化有助於我們對決策樹的理解和認識。利用強大的Matplotlib 庫就可以解決實際的需求。

1 生成決策樹的完整的代碼

新建一個test.py 文件，用於寫決策樹的建立代碼

  1 # coding=utf-8
  2 from math import log
  3 import operator
  4 def calcShannonEnt(dataSet):
  5     numEntries = len(dataSet)
 
  6     labelCounts = {}
  7     for featVec in dataSet:
  8         currentLabel = featVec[-1] # 提取類標號的屬性值
  9         # 把類標號不同的屬性值及其個數存入字典中
 10         if currentLabel not in labelCounts .keys():
 11             labelCounts [currentLabel ]=0
 12         labelCounts [currentLabel]+=1
 13     shannonEnt = 0.0
 14
 
     # 計算類標號的平均信息量，如公式中H（S）
 15     for key in labelCounts :
 16         prob = float(labelCounts [key])/numEntries
 17         shannonEnt -= prob * log(prob,2)
 18     return shannonEnt
 19 
 20 def createDataSet():
 21     dataSet = [[1, 1, ‘yes‘],
 22                [1, 1, ‘yes‘],
 23                [1, 0, ‘
 
no‘],
 24                [0, 1, ‘no‘],
 25                [0, 1, ‘no‘]]
 26     labels = [‘no surfacing‘,‘flippers‘]
 27     #change to discrete values
 28     return dataSet, labels
 29 def createDataSet1():
 30     dataSet = [[u‘小於等於5‘,u‘高‘,u‘否‘,u‘一般‘,u‘否‘],
 31                [u‘小於等於5‘, u‘高‘, u‘否‘, u‘好‘, u‘否‘],
 32                [u‘5到10‘, u‘高‘, u‘否‘, u‘一般‘, u‘否‘],
 33                [u‘大於等於10‘, u‘中‘, u‘否‘, u‘一般‘, u‘是‘],
 34                [u‘大於等於10‘, u‘低‘, u‘是‘, u‘一般‘, u‘是‘],
 35                [u‘5到10‘, u‘中‘, u‘否‘, u‘好‘, u‘否‘],
 36                [u‘5到10‘, u‘高‘, u‘是‘, u‘一般‘, u‘是‘],
 37                [u‘小於等於5‘, u‘中‘, u‘否‘, u‘一般‘, u‘否‘],
 38                [u‘5到10‘, u‘中‘, u‘否‘, u‘好‘, u‘否‘],
 39                [u‘大於等於10‘, u‘高‘, u‘是‘, u‘好‘, u‘是‘],
 40                [u‘5到10‘, u‘低‘, u‘是‘, u‘一般‘, u‘是‘],
 41                [u‘小於等於5‘, u‘中‘, u‘是‘, u‘一般‘, u‘是‘],
 42                [u‘小於等於5‘, u‘低‘, u‘是‘, u‘一般‘, u‘是‘],
 43                [u‘大於等於10‘, u‘中‘, u‘是‘, u‘好‘, u‘是‘]]
 44     labels = [u‘役齡‘,u‘價格‘,u‘是否關鍵部件‘,u‘磨損程度‘]
 45     return dataSet ,labels
 46 
 47 # 按照給定特征劃分數據集,把符合給定屬性值的對象組成新的列表
 48 def splitDataSet(dataSet,axis,value):
 49     retDataSet = []
 50     for featVec in dataSet:
 51         # 選擇符合給定屬性值的對象
 52         if featVec[axis] == value:
 53             reduceFeatVec = featVec[:axis] # 對對象的屬性值去除給定的特征的屬性值
 54             reduceFeatVec.extend(featVec[axis+1:])
 55             retDataSet.append(reduceFeatVec ) # 把符合且處理過的對象添加到新的列表中
 56     return retDataSet
 57 
 58 # 選取最佳特征的信息增益，並返回其列號
 59 def chooseBestFeaturesplit(dataSet):
 60     numFeatures = len(dataSet[0])-1  # 獲得樣本集S 除類標號之外的屬性個數，如公式中的k
 61     baseEntropy = calcShannonEnt(dataSet)  # 獲得類標號屬性的平均信息量，如公式中H(S)
 62 
 63     bestInfoGain = 0.0 # 對最佳信息增益的初始化
 64     bestFeature = -1 # 最佳信息增益的屬性在樣本集中列號的初始化
 65 
 66     # 對除類標號之外的所有樣本屬性一一計算其平均信息量
 67     for i in range(numFeatures ):
 68         featList = [example[i] for example in dataSet] # 提取第i 個特征的所有屬性值
 69         uniqueVals = set(featList ) # 第i 個特征所有不同屬性值的集合，如公式中 aq
 70         newEntropy = 0.0 # 對第i 個特征的平均信息量的初始化
 71         # 計算第i 個特征的不同屬性值的平均信息量，如公式中H（S| Ai）
 72         for value in uniqueVals:
 73             subDataSet = splitDataSet(dataSet,i,value ) # 提取第i 個特征，其屬性值為value的對象集合
 74             prob = len (subDataSet )/float(len(dataSet)) # 計算公式中P（Cpq）的概率
 75             newEntropy += prob * calcShannonEnt(subDataSet ) # 第i個特征的平均信息量，如 公式中H（S| Ai）
 76         infoGain = baseEntropy - newEntropy  # 第i 個的信息增益量
 77         if (infoGain > bestInfoGain  ): # 選取最佳特征的信息增益，並返回其列號
 78             bestInfoGain   = infoGain
 79 
 80             bestFeature = i
 81     return bestFeature
 82 
 83 # 選擇列表中重復次數最多的一項
 84 def majorityCnt(classList):
 85     classCount= {}
 86     for vote in classList :
 87         if vote not in classCount .keys():
 88             classCount [vote] =0
 89         classCount[vote] += 1
 90     sortedClassCount = sorted(classCount.iteritems() ,
 91                                   key=operator.itemgetter(1),
 92                                   reverse= True ) # 按逆序進行排列，並返回由元組組成元素的列表
 93     return sortedClassCount[0][0]
 94 
 95 # 創建決策樹
 96 def createTree(dataSet,labels):
 97     Labels = labels [:]  # 防止改變最初的特征列表
 98     classList = [example[-1] for example in dataSet ] # 獲得樣本集中的類標號所有屬性值
 99     if classList.count(classList [0]) == len(classList): # 類標號的屬性值完全相同則停止繼續劃分
100         return classList[0]
101     if len(dataSet[0]) == 1: # 遍歷完所有的特征時，仍然類標號不同的屬性值，則返回出現次數最多的屬性值
102         return majorityCnt(classList)
103     bestFeat = chooseBestFeaturesplit(dataSet) # 選擇劃分最佳的特征,返回的是特征在樣本集中的列號
104     bestFeatLabel = Labels[bestFeat]  # 提取最佳特征的名稱
105     myTree = {bestFeatLabel :{}} # 創建一個字典，用於存放決策樹
106     del(Labels[bestFeat]) # 從特征列表中刪除已經選擇的最佳特征
107     featValues = [example[bestFeat] for example in dataSet ] # 提取最佳特征的所有屬性值
108     uniqueVals = set(featValues ) # 獲得最佳特征的不同的屬性值
109     for value in uniqueVals :
110         subLabels = Labels[:] #  把去除最佳特征的特征列表賦值於subLabels
111         myTree [bestFeatLabel][value] = createTree(splitDataSet(dataSet ,bestFeat ,value ),
112                                                    subLabels ) # 遞歸調用createTree()
113     return myTree
114 
115 # 決策樹的存儲
116 def storeTree(inputTree,filename):
117     import pickle
118     fw = open(filename,‘w‘)
119     pickle.dump(inputTree ,fw)
120     fw.close()
121 
122 def grabTree(filename):
123     import pickle
124     fr = open(filename)
125     return pickle.load(fr)
126 
127 
128 # 使用決策樹的分類函數
129 def classify(inputTree,featLabels,testVec):
130     firstStr = inputTree.keys()[0]  # 獲得距離根節點最近的最佳特征
131     secondDict = inputTree[firstStr ]  # 最佳特征的分支
132     featIndex = featLabels .index(firstStr) # 獲取最佳特征在特征列表中索引號
133     for key in secondDict .keys(): # 遍歷分支
134         if testVec [featIndex ] == key: # 確定待查數據和最佳特征的屬性值相同的分支
135             if type(secondDict [key]).__name__ == ‘dict‘: # 判斷找出的分支是否是“根節點”
136                 classLabel = classify(secondDict[key],featLabels ,testVec) # 利用遞歸調用查找葉子節點
137             else:
138                 classLabel  = secondDict [key]  # 找出的分支是葉子節點
139     return classLabel

2 決策樹的圖形可視化

另外新建一個文件 treeplotter.py , 編寫決策樹圖形可視化的代碼。

 1 # coding=utf-8
 2 import matplotlib.pyplot as plt
 3 import sys
 4 import test
 5 reload(sys)
 6 sys.setdefaultencoding(‘utf-8‘)
 7 decisionNode = dict(boxstyle="sawtooth", fc="0.8")
 8 leafNode = dict(boxstyle="round4", fc="0.8")
 9 arrow_args = dict(arrowstyle="<-")
10 
11 # 獲得葉子節點的數目
12 def getNumLeafs(myTree):
13     numLeafs = 0
14     firstStr = myTree.keys()[0]
15     secondDict = myTree[firstStr]
16     for key in secondDict.keys():
17         if type(secondDict[key]).__name__==‘dict‘:#test to see if the nodes are dictonaires, if not they are leaf nodes
18             numLeafs += getNumLeafs(secondDict[key])
19         else:   numLeafs +=1
20     return numLeafs
21 
22 # 獲得決策樹的層數
23 def getTreeDepth(myTree):
24     maxDepth = 0
25     firstStr = myTree.keys()[0]
26     secondDict = myTree[firstStr]
27     for key in secondDict.keys():
28         if type(secondDict[key]).__name__==‘dict‘:#test to see if the nodes are dictonaires, if not they are leaf nodes
29             thisDepth = 1 + getTreeDepth(secondDict[key])
30         else:   thisDepth = 1
31         if thisDepth > maxDepth: maxDepth = thisDepth
32     return maxDepth
33 
34 def plotNode(nodeTxt, centerPt, parentPt, nodeType):
35     createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords=‘axes fraction‘,
36              xytext=centerPt, textcoords=‘axes fraction‘,
37              va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
38     
39 def plotMidText(cntrPt, parentPt, txtString):
40     xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
41     yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
42     createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
43 
44 def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
45     numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
46     depth = getTreeDepth(myTree)
47     firstStr = myTree.keys()[0]     #the text label for this node should be this
48     cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
49     plotMidText(cntrPt, parentPt, nodeTxt)
50     plotNode(firstStr, cntrPt, parentPt, decisionNode)
51     secondDict = myTree[firstStr]
52     plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
53     for key in secondDict.keys():
54         if type(secondDict[key]).__name__==‘dict‘:#test to see if the nodes are dictonaires, if not they are leaf nodes   
55             plotTree(secondDict[key],cntrPt,str(key))        #recursion
56         else:   #it‘s a leaf node print the leaf node
57             plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
58             plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
59             plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
60     plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
61 #if you do get a dictonary you know it‘s a tree, and the first element will be another dict
62 
63 def createPlot(inTree):
64     fig = plt.figure(1, facecolor=‘white‘)
65     fig.clf()
66     axprops = dict(xticks=[], yticks=[])
67     createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
68     #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
69     plotTree.totalW = float(getNumLeafs(inTree))
70     plotTree.totalD = float(getTreeDepth(inTree))
71     plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
72     plotTree(inTree, (0.5,1.0), ‘‘)
73     plt.show()
74 
75 
76 if __name__ == ‘__main__‘:
77     dataSet, labels = test.createDataSet1()
78     myTree = test.createTree(dataSet, labels)
79     createPlot(myTree)

3 運行結果顯示

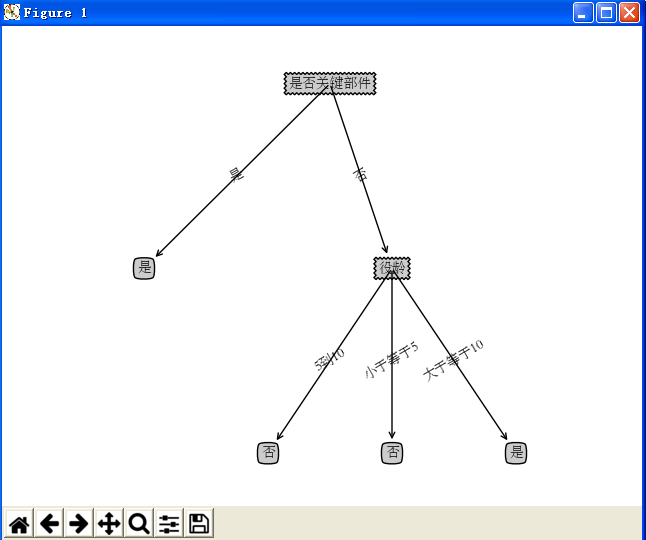
決策樹的圖形可視化