皇後問題

題目描述:

有一個n*n的棋盤，你要在這個棋盤上放上n個皇後，使得她們不能相互攻擊。當然為了使得問題更加有趣，我們在棋盤上限定了一些位置使得這些位置上不能放皇後。

輸入格式:

第一行兩個數n和m ，表示在一個n*n的棋盤上放n個皇後，有m個受限位置。

接下來m行每行兩個數，x和y，表示第x行，第y列這個位置不可以放皇後。

輸出格式:

一行一個數 ans，表示總的方案數。

樣例輸入:

4 1
1 2

樣例輸出:

1

樸素算法（60分）

#include<iostream>
using namespace std;
int n,m,b[20][20],l[20],pi[40],na[40
 
],x,y,ans;
int DFS(int i){
    if(i==n+1){ans++;return 0;}
    for(int j=1;j<=n;j++){
        if(b[i][j]==0 && l[j]==0 && pi[i+j]==0 && na[i-j+n]==0){
            l[j]=1;
            pi[i+j]=1;
            na[i-j+n]=1;
            DFS(i+1);
            l[j]=0;
            pi[i+j]=0
 
;
            na[i-j+n]=0;
        }
    }
    return 0;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        b[x][y]=1;
    }
    DFS(1);
    cout<<ans<<endl;
}

高級算法（位運算）（100分）

#include<iostream>
using namespace std;
int n,m,x,y,ans,a[20
 
];
void DFS(int row,int ld,int rd,int h)
{
    if(row!=(1 << n) - 1){
        int pos=((1<<n)-1)&~(row|ld|rd|a[h]);
        while(pos){
            int p=pos & -pos;
            pos-=p;
            DFS(row+p,(ld+p)<<1,(rd+p)>>1,h+1);
        }
    }
    else ans++;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        a[x]+=1<<(y-1);
    }
    DFS(0,0,0,1);
    cout<<ans<<endl;
}

高級算法（位運算）思路：

初始化：　upperlim = (1 << n)-1; Ans = 0;
調用參數：test(0, 0, 0);
和普通算法一樣，這是一個遞歸函數，程序一行一行地尋找可以放皇後的地方。函數帶三個參數row、ld和rd，分別表示在縱列和兩個對角線方向的限制條件下這一行的哪些地方不能放。位於該行上的沖突位置就用row、ld和rd中的1來表示。把它們三個並起來，得到該行所有的禁位，取反後就得到所有可以放的位置（用pos來表示）。 p = pos & (~pos + 1)其結果是取出最右邊的那個1。這樣，p就表示該行的某個可以放子的位置，把它從pos中移除並遞歸調用test過程。 註意遞歸調用時三個參數的變化，每個參數都加上了一個禁位，但兩個對角線方向的禁位對下一行的影響需要平移一位。最後，如果遞歸到某個時候發現row=upperlim了，說明n個皇後全放進去了，找到的解的個數加一。

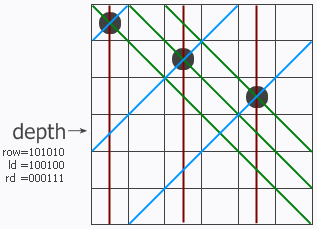
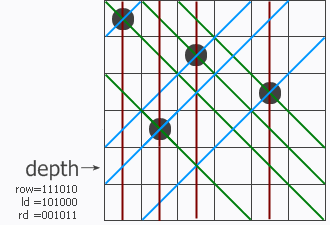
註：

upperlime：=（1 << n）-1 就生成了n個1組成的二進制數。

這個程序是從上向下搜索的。

pos & -pos 的意思就是取最右邊的 1 再組成二進制數，相當於 pos &（~pos +1），因為取反以後剛好所有數都是相反的（怎麽聽著像廢話），再加 1 ，就是改變最低位，如果低位的幾個數都是1，加的這個 1 就會進上去，一直進到 0 ，在做與運算就和原數對應的 1 重合了。舉例可以說明：

原數 0 0 0 0 1 0 0 0 原數 0 1 0 1 0 0 1 1

取反 1 1 1 1 0 1 1 1 取反 1 0 1 0 1 1 0 0

加1 1 1 1 1 1 0 0 0 加1 1 0 1 0 1 1 0 1

與運算 0 0 0 0 1 0 0 0 and 0 0 0 0 0 0 0 1

其中呢，這個取反再加 1 就是補碼，and 運算 與負數，就是按位和補碼與運算。

(ld | p)<< 1 是因為由ld造成的占位在下一行要右移一下；

(rd | p)>> 1 是因為由rd造成的占位在下一行要左移一下。

ld rd row 還要和upperlime 與運算 一下，這樣做的結果就是從最低位數起取n個數為有效位置，原因是在上一次的運算中ld發生了右移，如果不and的話，就會誤把n以外的位置當做有效位。

皇後問題(DFS)(位運算)