題目要求把整數集P的元素分成兩部分A與B，A集要求若x在其中，則a-x也必須在其中，B集要求若x在其中，則b-x也必須在其中。這個問題可以建模成一個二分圖的完美匹配問題。二分圖的左右兩個點集都是P，將x與a-x（若存在）連線，將x與b-x（若存在）連線，所求問題就是找該二分圖的完美匹配。但是此題如此構造的二分圖很特殊，每個頂點的度數至多為2，且連線有限制。所以除了使用二分圖完美匹配的通用算法之外，還可以考慮更簡單快速的特殊算法。

不妨假設a<b，P為整數集。對P中的元素x，分別稱a-x、b-x為x的a補、b補。首先，我們知道，對元素x，若既不存在a補也不存在b補，直接輸出“NO”。若只存在a補和b補中的一個，則x與這個補元必定要放到相應的A或B。若a補和b補均存在，這是比較麻煩的情況，我們要決定x到底該放入A還是B。比如a=10，b=12。如果P={4,6,8}，則A={}，B={4,6,8}。如果P={4,6,8,2}，則A={4,6,8,2}，B={}。所以x=4放入A或B都有可能。

為此，先對P中的元素從小到大排序，然後看最小元x，如果x只有一個補元，容易決定x該放入哪個集合。如果這個最小元x的a補和b補都存在呢？有如下結論：x的b補不可能有a補了！（如下圖所示）用反證法可證：假設y是b補的a補，即y=a-(b-x)=a-b+x<x，與x是最小元的事實矛盾。

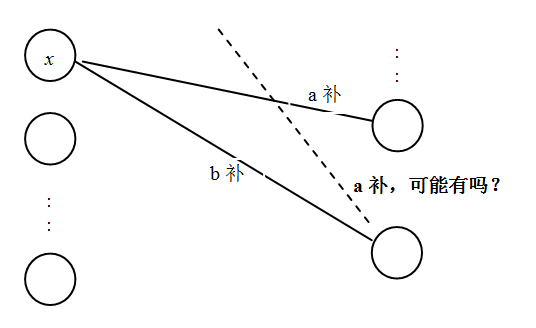
所以在最小元的a補和b補均存在的情況下，雖然不能決定x放哪裏，但是可以決定x的b補放哪裏，它必定只有b補，故可將b-x以及x一起放入B。然後對P的剩余元素再從最小元開始進行上述檢查操作，直至P空為止。

算法需要先對P排序，然後對P進行一趟掃描，每個x需要查找兩個補元，二分查找需要O(logn)時間，所以算法的計算復雜性是O(nlogn)。

如果a=b，簡單地檢查每個元素x，看a-x是否也在P中即可。

參考代碼：

#include <stdio.h>
#include <set>
#include <vector>
using namespace std;

int main()
{
    int n, a, b, x;
    set<int> P, A;
    set<int>::const_iterator it;
    vector<int> V;
    vector<int>::const_iterator itv;
    
 
bool swap, b1, b2;
        
    scanf("%d%d%d", &n, &a, &b);
    for (int i = 0; i < n; i++) {
        scanf("%d", &x);
        P.insert(x);
        V.push_back(x);
    }
    swap = 0;
    if (a == b) {
        for (it = P.begin(); it != P.end(); it++) {
            x = *it;
            if (P.find(a-x) == P.end()) {
                printf("NO\n");
                return 0;
            }
        }
        A = P;
    } else {
        if (a > b) {
            int t = a;
            a = b;
            b = t;
            swap = 1;
        }
        while (!P.empty()) {
            x = *P.begin();
            b1 = (P.find(a-x) != P.end());
            b2 = (P.find(b-x) != P.end());
            if (!b1 && !b2) {    // x沒有補元 
                printf("NO\n");
                return 0;
            } else if (b1 && b2) {    // x有兩個補元 
                P.erase(x);
                P.erase(b-x);
            } else {    // x恰有一個補元 
                P.erase(x);
                if (b1) {
                    P.erase(a-x);
                    A.insert(x);
                    A.insert(a-x);
                } else {
                    P.erase(b-x);
                }
            }
        }
    }
    printf("YES\n");
    for (itv = V.begin(); itv != V.end(); itv++)
        printf("%d ", (A.find(*itv) == A.end() ? 1 : 0) ^ swap);
    printf("\n");
    return 0;
}

CodeForces468B Two Sets 解題報告