實驗四-圖的實現與應用

圖的實現與應用-1

實驗要求：

用鄰接矩陣實現無向圖（邊和頂點都要保存），實現在包含添加和刪除結點的方法，添加和刪除邊的方法，size(),isEmpty()，廣度優先叠代器，深度優先叠代器

實驗過程：

1. 用二維數組構建鄰接矩陣
2. 添加刪除邊的方法和添加頂點的方法的較為簡單，在此不做介紹
3. （重點）刪除頂點：利用兩個for循環；外層循環遍歷列，內層循環遍歷排。
   偽代碼如下：

public void removevertice(int A){
for（int i = 0； i < 數組長度;i++）{
    for（int i = 0； i < 數組長度;i++){
        if (i 等於 A 並且 該二維數組的值為真)
        該二維數組的值為假
        if(s 等於 A)
        該二維數組的值為假
    }
}
}
 

4.廣度遍歷：參考書上代碼：在書上代碼的基礎進行微調。偽代碼：

定義一個數組visited，用於存放已標記頂點
for 將頂點放入visited數組中並將其標註為未訪問
將頂點入隊並標記為已訪問
while（隊列不為空）｛
從隊列中取出第一個頂點，並將頂點放入list中
，將當前頂點中未被標記為以訪問的所有鄰接點入隊，同時將這些頂點標記為已訪問
｝

5.深度遍歷：用棧替換隊列

實驗結果：

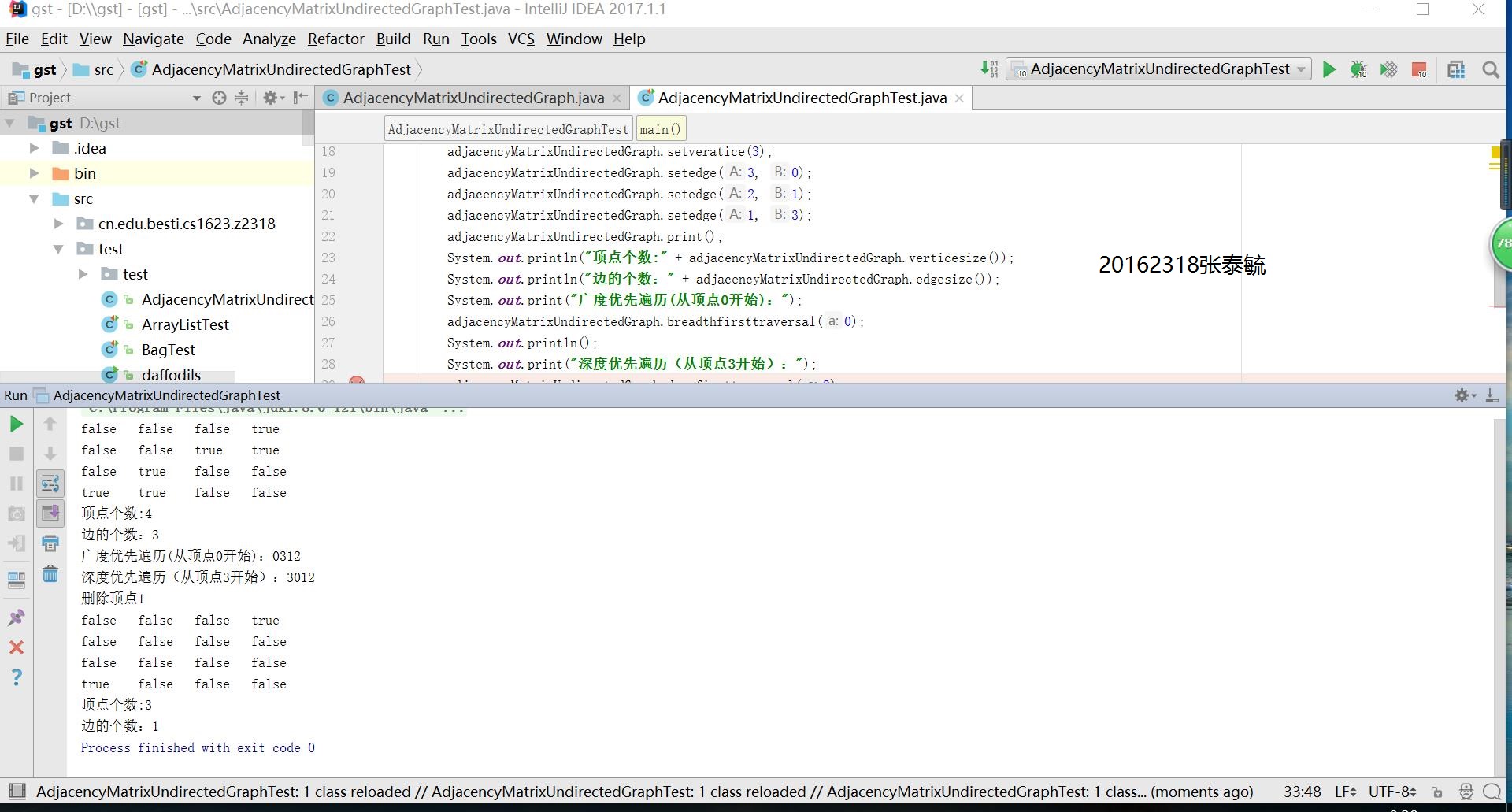
代碼鏈接

圖的實現與應用-2

實驗要求：

用十字鏈表實現無向圖（邊和頂點都要保存），實現在包含添加和刪除結點的方法，添加和刪除邊的方法，size(),isEmpty()，廣度優先叠代器，深度優先叠代器

實驗過程：

剛開始對十字鏈表這個結構不是十分的了解，簡單的來說十字鏈表就是兩個鏈表結合在一塊，織成一張網。或者可以這樣理解：它其實也是一個鄰接矩陣，只不過它是特殊的：

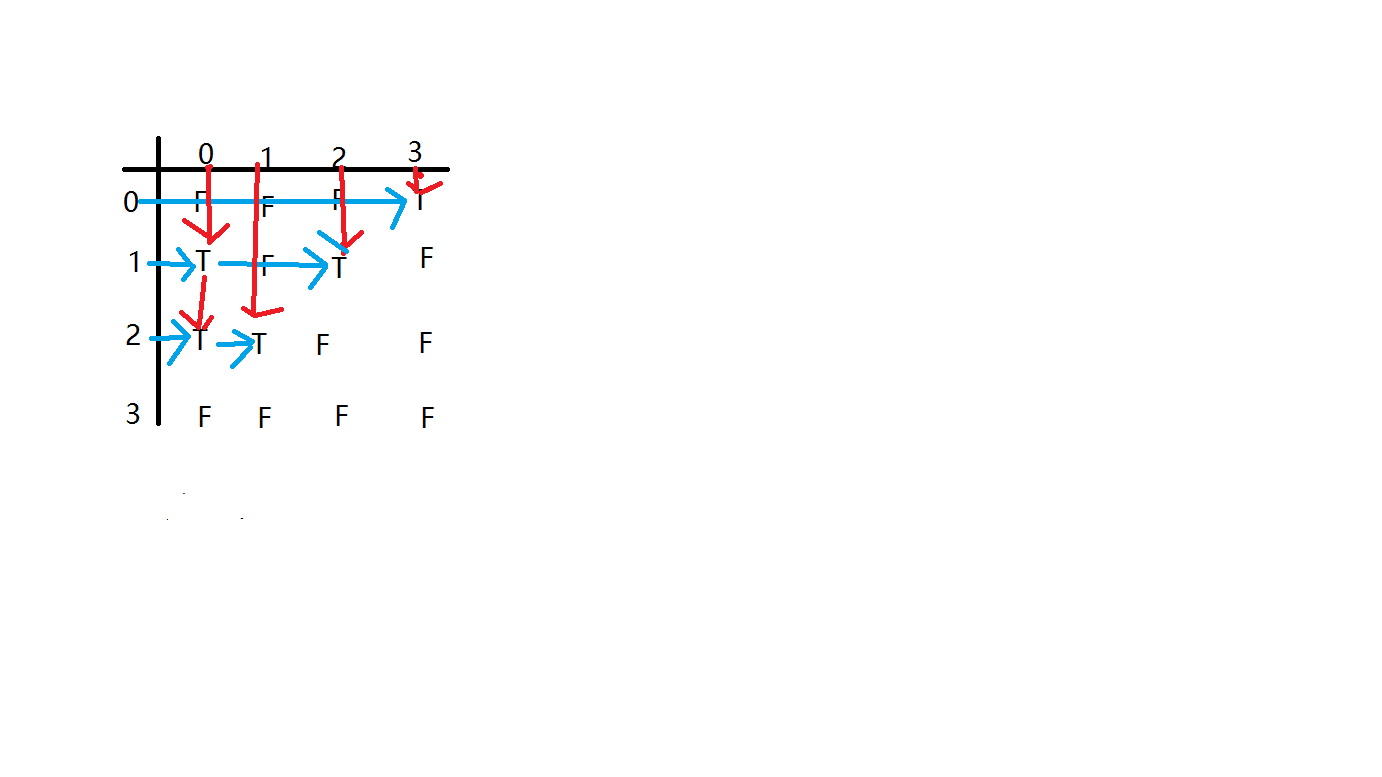
定義頂點結構：

定義邊結構：

構件圖思路與構建鏈表的思路換湯不換藥，其中較為麻煩的便是刪除頂點，下面給出源代碼：

public void removeVertic(VertexNode node) {
        list.remove(node.getVertex());
        EdgeNode edgeNode1 = node.firstOut;
        EdgeNode edgeNode2 = node.firsstIn;
        while (edgeNode1 != null) {
            removeEdge(edgeNode1);  //刪除邊
            edgeNode1 = edgeNode1.taillink;
        }
        while (edgeNode2 != null) {
            removeEdge(edgeNode2); //刪除邊
            edgeNode2 = edgeNode2.headllink;

        }
    }
 

實驗結果：

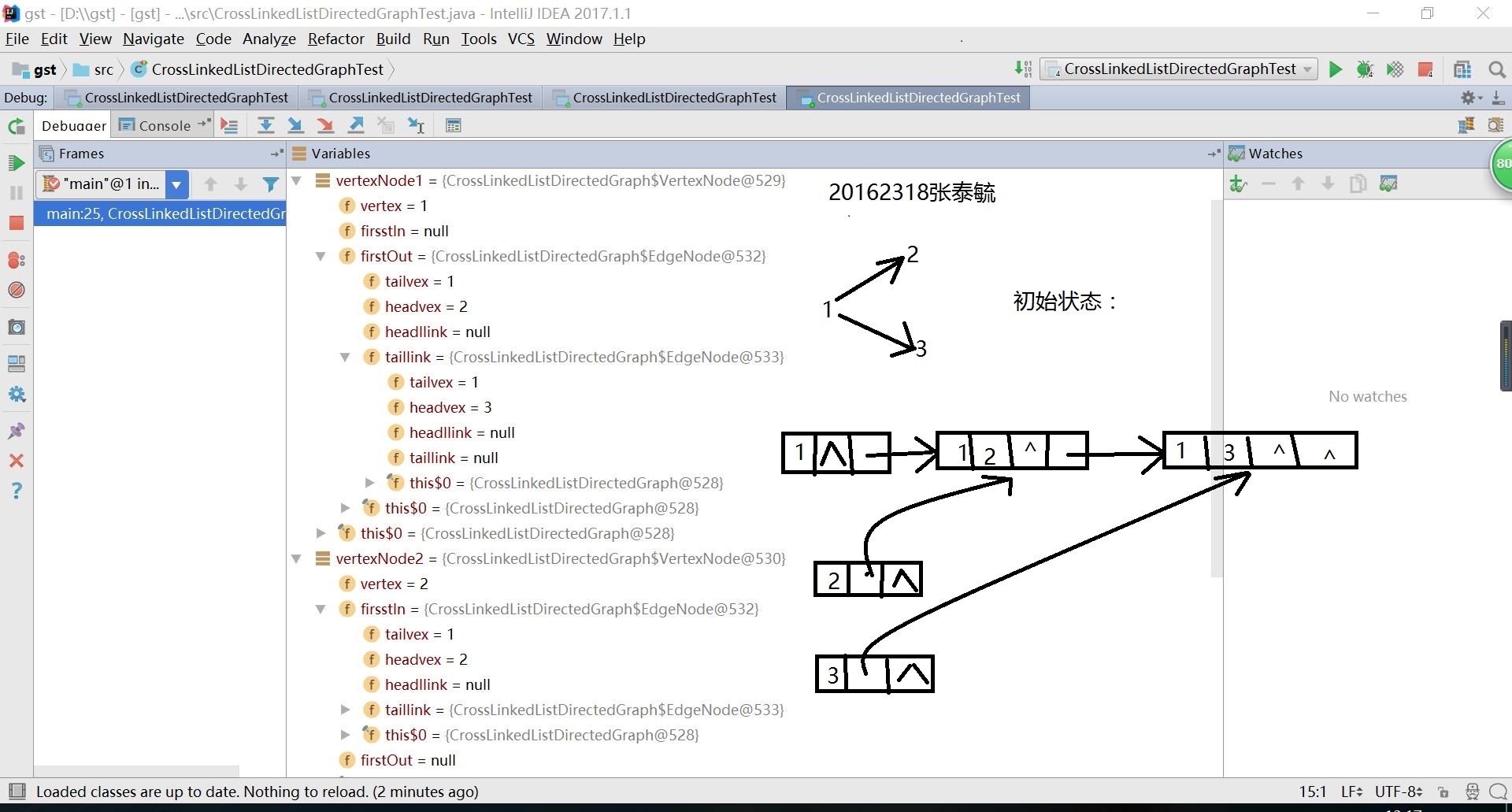
代碼鏈接

圖的實現與應用-3

實驗要求：

實現PP19.9

實驗過程

此題我選用弗洛伊德算法

弗洛伊德算法：通過一個圖的權值矩陣求出它的每兩點間的最短路徑矩陣。

偽代碼：

（1）設Dist(u, v)為結點u到結點v的距離，中間點w，
（2）若有Dist(u, w) + Dis(w, v) < Dis(u, v)，則Dis(u, v) = Dis(u, w) + Dis(w, v)，
（3）遍歷所有頂點w，Dis(u, v)中記錄的便是u到v的最短路徑的距離

核心代碼：

for (int k = 0; k < dis.length; k++) {
            for (int i = 0; i < dis.length; i++) {
                for (int j = 0; j < dis.length; j++) {
                    int mn = dis[i][j];
                    int mk = dis[i][k];
                    int kn = dis[k][j];
                    int addedPath = (mk == MAX_WEIGHT || kn == MAX_WEIGHT) ? MAX_WEIGHT : mk + kn;

                    if (mn > addedPath) {
                        //如果經過k頂點路徑比原兩點路徑更短，將兩點間權值設為更小的一個
                        dis[i][j] = addedPath;
                        //前驅設置為經過下標為k的頂點
                        path[i][j] = path[i][k];
                    }
                }
            }
        }

實驗結果：

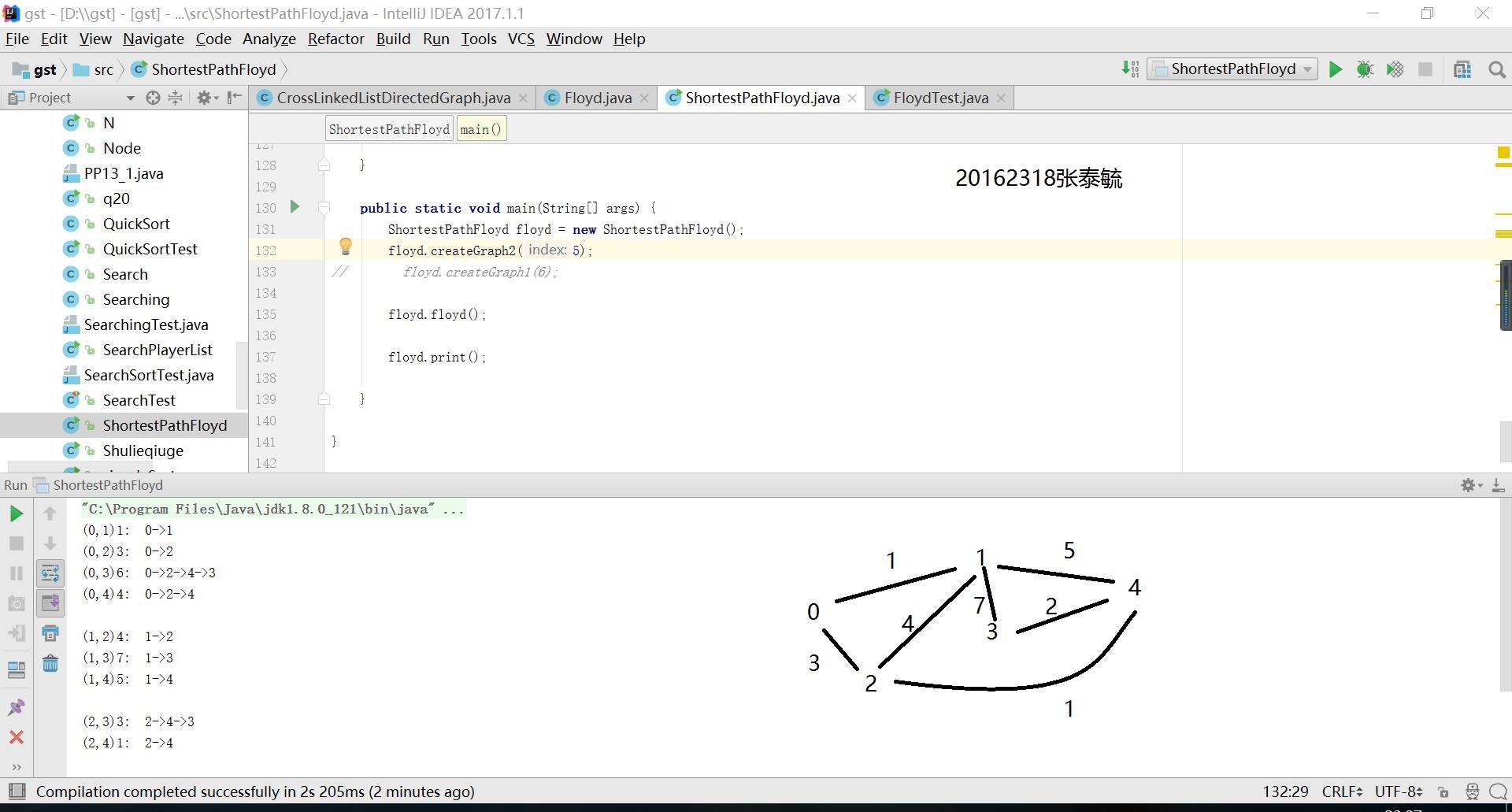
代碼鏈接

實驗四-圖的實現與應用