當數組基本有序時，插入排序法效率很高，而希爾排序法就是充分利用插入排序法這一特長的高速算法。希爾排序法中，程序會重復進行以間隔為g的元素為對象的插入排序。

設g的集合為G，集合G中的數一般是降序排列，最後一個數必須為1。具體流程如下：

• 對集合G中的每一個g，執行如下操作：

1. 將數組中以g為間隔的數使用插入排序法進行排序

以數組{4, 8, 9, 1, 10, 6, 2, 5, 3, 7}進行G={4, 3, 1}為例使用希爾排序，過程如下圖所示：

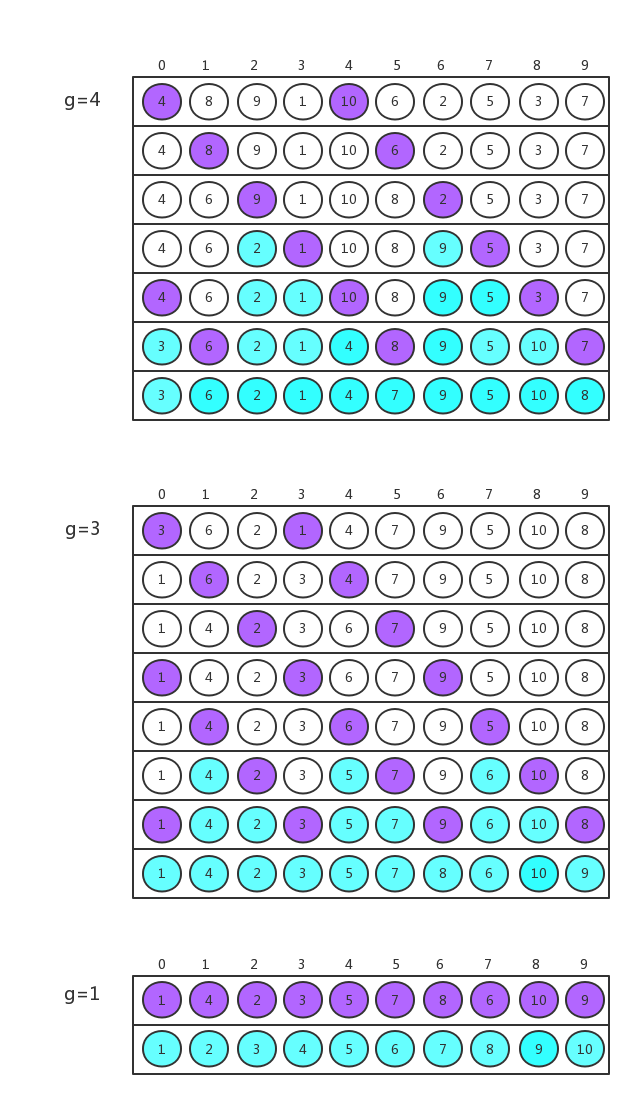
圖中的紫色表示每次要排序的序列，藍色表示在一次間隔中確定位置的數。要註意的一點是，程序的處理順序與組的順序無關。

g的選擇方法很多，例如：當g=1, 4, 13, 40···即\(g_{n+1}=3*g_{n}+1\)

參考代碼如下：

    import java.util.ArrayList;
    import java.util.List;

    //希爾排序
    //插入排序法可以高速處理順序較整齊的數據，而希爾排序法就是充分發揮插入排序法這一特長的高速算法。
    public static void shellSort(int[] num){
        if (num==null || num.length==0)
            return;

        //生成數組G，表示間隔。因為G的大小不能確定，所以使用list
        List<Integer> G = new ArrayList<>();
        int h = 1;
        while (h<num.length){
            G.add(h);
            h = 3*h + 1;
        }

        for (int i=G.size()-1; i>=0; i--){
            insertionSortShell(num, G.get(i));
        }
    }

    public static void insertionSortShell(int[] num, int g){
        for (int i=g; i<num.length; i++){
            int temp = num[i];
            int j = i-g;
            while (j>=0 && num[j]>temp){
                num[j+g] = num[j];
                j -= g;
            }
            num[j+g] = temp;
        }
    }
 

希爾排序不是穩定排序，時間復雜度也因g的選取和數組序列的順序的不同而不同。

希爾排序法