4. 推斷

高效的推斷算法對條件隨機場的訓練和序列預測都非常重要。主要有兩個推斷問題：第一，模型訓練之後，為新的輸入\(\mathbf{x}\)確定最可能的標記\(\mathbf{y}^* = \arg \max_{\mathbf{y}} p(\mathbf{y}|\mathbf{x})\)；第二，如第5部分所述，參數估計常要求計算標記子集上的邊緣分布，例如節點的的邊緣分布\(p(y_t|\mathbf{x})\)和邊上的邊緣分布\(p(y_t,y_{t-1}|\mathbf{x})\)。這兩個推斷問題可被看作同一基本問題上的兩個不同的操作過程[1]。也就是說，若要將求邊緣分布問題轉化為最大化問題，僅需要將求和換作求最大化即可。

對於離散的變量，邊緣分布可以通過暴力求和來計算，但是計算量會隨著\(Y\)的增大指數增長。實際上，兩個推斷問題在任意圖結構上都不容易，因為任何命題的可滿足性問題（propositional satisfiability problem）都可以很容易地表示為一個因子圖。

在線性鏈條件隨機場中，兩種推斷問題都有高效、精確的動態規劃方法（僅需對HMM中的動態規劃方法稍作變動）。我們首先介紹這些方法——計算邊緣分布的前向後向算法和計算輸出序列的維特比算法（4.1節）。這兩個算法是樹結構圖模型中信念傳播算法（belief propagation algorithm）的特例。對於更復雜的模型，則需要使用近似推斷。

從某種意義上來說，條件隨機場的推斷問題也其他圖模型沒什麽不同，因此可以使用任何圖模型的推斷算法，如文獻[57,79]。不過，在條件隨機場中，需要記住兩個問題。第一個問題，推斷子程序在參數估計過程中會被重復調用（原因見5.1.1節），其計算量是指數級的，因此我們需要在計算精度和效率之間進行權衡。第二個問題，如果使用了近似推斷，推斷過程和參數估計過程可能會產生復雜的相互影響作用。我們在第5部分中介紹參數估計時再討論這個問題，但是在這裏也需要註意它，因為它會嚴重影響對推斷算法的選擇。

4.1 線性鏈條件隨機場

本節，我們簡要回顧HMM的標準推斷算法，前向-後向算法和維特比算法，並且討論它們在條件隨機場中的應用。關於HMM中的這些算法參見綜述文獻Rabiner[111]。這兩個算法都是4.2.2節中的信念傳播算法的特例。我們對線性鏈算法進行深入分析，一方面使得下文的分析更具體，另一方面它們在實際中的確非常有用。

首先，我們介紹簡化前向-後向叠代算法中所用的符號。HMM可被看作一個因子圖\(p(\mathbf{y},\mathbf{x})=\prod_t \Psi_t(y_t,y_{t-1},x_t)\)，其中\(Z=1\)，因子定義為：
\[ \Psi_t(j,i,x)\overset{\text{def}}{=}p(y_t=j | y_{t-1}=i)p(x_t=x|y_t=j). \tag{4.1} \]
如果HMM被看作加權有限狀態機（weighted finite state machine），那麽\(\Psi_t(j,i,x)\)為當前觀測為\(x\)時狀態\(i\)向狀態\(j\)轉移的權值。

現在我們回顧HMM的前向算法，用於計算觀測概率\(p(\mathbf{x})\)。前向-後向算法背後的思想是首先利用下面的分配律重寫樸素假設\(p(\mathbf{x})=\sum_{\mathbf{y}}p(\mathbf{x},\mathbf{y})\)：
\[ \begin{align} p(\mathbf{x})&=\sum_{\mathbf{y}}\prod_{t=1}^T \Psi_t(y_t,y_{t-1},x_t) \tag{4.2} \&= \sum_{y_T}\left\{ \sum_{y_{T-1}} \left\{ \Psi_T(y_T, y_{T-1}, x_T) \sum_{y_{T-2}}\left\{ \Psi_{T-1}(y_{T-1},y_{T-2},x_{T-1}) \sum_{y_{T-3}} \cdots \right\}\right\}\right\} \tag{4.3} \end{align} \]

原文式中沒有花括號

觀察上式，可知式中的每個求和都會被外部的求和使用多次，因此若能將內部求和結果保存下來將能夠節省指數級的計算量。

於是，定義前向變量\(\alpha_t\)為長度為\(M\)的向量（\(M\)為狀態的數量），用於表示式（4.3）內部的求和。定義為：
\[ \begin{align} \alpha_t(j) & \overset{\text{def}}{=} p(\mathbf{x}_{\langle 1 \dots t \rangle}, y_t = j) \tag{4.4} \&= \sum_{\mathbf{y}_{\langle 1 \dots t-1\rangle}} \Psi_t(j,y_{t-1}, x_t) \prod_{t‘=1}^{t-1}\Psi_{t‘}(y_{t‘}, y_{t‘-1}, x_{t‘}), \tag{4.5} \end{align} \]
其中，\(\mathbf{y}_{\langle 1\dots t-1 \rangle}\)上的求和範圍為隨機變量\(y_1,y_2,\dots,y_{t-1}\)上的所有取值。\(\alpha\)的值可以用叠代方式求解
\[ \alpha_t(j)=\sum_{i\in S} \Psi_t(j,i,x_t)\alpha_{t-1}(i), \tag{4.6} \]
初始值為\(\alpha_1(j)=\Psi_1(j,y_0,x_1)\)。（回想式（2.10），\(y_0\)為HMM中的初始狀態）。於是，\(p(\mathbf{x})=\sum_{y_T} \alpha_T(y_T)\)。將式（4.6）代入並遞歸替換，可得到式（4.3）。數學歸納法可給出嚴格的證明。

反向遞歸過程基本一樣，區別在於按相反的順序處理式（4.3）中的求和。定義
\[ \begin{align} \beta_t(i) &\overset{\text{def}}{=}p(\mathbf{x}_{\langle t+1 \dots T\rangle}|y_t=i) \tag{4.7}\&= \sum_{\mathbf{y}_{\langle t+1\dots T\rangle}} \prod_{t‘=t+1}^T \Psi_{t‘}(y_{t‘}, y_{t‘-1}, x_{t‘}), \tag{4.8} \end{align} \]
叠代公式
\[ \beta_t(i)=\sum_{j \in S} \Psi_{t+1}(j,i,x_{t+1})\beta_{t+1}(j), \tag{4.9} \]
其中初始值\(\beta_T(i)=1\)。與前向過程類似，也可以利用後向變量計算\(p(\mathbf{x})=\beta_0(y_0)\overset{\text{def}}{=}\sum_{y_1}\Psi_1(y_1,y_0,x_1)\beta_1(y_1)\)。

為了計算邊緣分布\(p(y_{t-1},y_t|\mathbf{x})\)（在參數估計中有重要應用），需要將前向叠代和後向叠代相結合。可以從概率的視角去分析，也可以從因子分解的角度去分析。首先，從概率的角度
\[ \begin{align} p(y_{t-1},y_t|\mathbf{x}) & = \frac{ p(\mathbf{x}|y_{t-1},y_t)p(y_{t-1},y_t) }{p(\mathbf{x})} \tag{4.10} \&= \frac{p(\mathbf{x}_{\langle 1 \dots t-1 \rangle}, y_{t-1}) p(y_t|y_{t-1}) p(x_t|y_t) p(\mathbf{x}_{\langle t+1 \dots T \rangle} | y_t) }{p(\mathbf{x})} \tag{4.11} \&= \frac{1}{p(\mathbf{x})} \alpha_{t-1}(y_{t-1}) \Psi_t(y_t, y_{t-1},x_t)\beta_t(y_t), \tag{4.12} \end{align} \]
其中，第二行利用了在給定\(y_{t-1}, y_t\)的條件下， \(\mathbf{x}_{\langle 1 \dots t-1 \rangle}\)與\(\mathbf{x}_{\langle t+1 \dots T \rangle}\)以及\(x_t\)相互獨立的事實。

註：$p(\mathbf{x}|y_{t-1},y_t) =p(\mathbf{x}{\langle 1 \dots t-1 \rangle}|y{t-1},y_t)p(x_t|y_{t-1},y_t)p(\mathbf{x}{\langle t+1 \dots T \rangle}|y{t-1},y_t) $，由於馬爾可夫假設及輸出僅依賴於當前狀態的假設，於是有如下三式成立：
\[ \begin{align} p(\mathbf{x}_{\langle 1 \dots t-1 \rangle}|y_{t-1},y_t)&=p(\mathbf{x}_{\langle 1 \dots t-1 \rangle}|y_{t-1}) = p(\mathbf{x}_{\langle 1 \dots t-1 \rangle},y_{t-1})\frac{1}{p(y_{t-1})} \p(x_t|y_{t-1},y_t)&=p(x_t|y_t) \p(\mathbf{x}_{\langle t+1 \dots T \rangle}|y_{t-1},y_t) &=p(\mathbf{x}_{\langle t+1 \dots T\rangle}|y_t) \end{align} \]
代入式（4.10）即可得到式（4.11）。

等價地，從因子分解的角度，應用分配率，可得
\[ \begin{align} p(y_{t-1},y_t|\mathbf{x}) = & \frac{1}{p(\mathbf{x})} \Psi_t(y_t,y_{t-1},x_t) \times \left( \sum_{\mathbf{y}_{\langle 1 \dots t-2 \rangle}} \prod_{t‘=1}^{t-1} \Psi_{t‘}(y_{t‘}, y_{t‘-1},x_{t‘}) \right) \& \times \left( \sum_{\mathbf{y}_{\langle t+1 \dots T \rangle}} \prod_{t‘=t+1}^T \Psi_{t‘}(y_{t‘}, y_{t‘-1},x_{t‘}) \right). \end{align} \tag{4.13} \]
利用\(\alpha\)和\(\beta\)的定義替換，可以得到同樣的結果，即
\[ p(y_{t-1},y_t|\mathbf{x})=\frac{1}{p(\mathbf{x})} \alpha_{t-1}(y_{t-1}) \Psi_t(y_t, y_{t-1},x_t)\beta_t(y_t). \tag{4.14} \]
因子\(1/p(\mathbf{x})\)為分布的歸一化常量。可以利用\(p(\mathbf{x})=\beta_0(y_0)\)或者\(p(\mathbf{x})=\sum_{i\in S}\alpha_T(i)\)求得。

綜合上述分析，前向-後向算法過程為：首先利用式（4.6）計算\(\alpha_t\)，然後利用式（4.9）計算\(\beta_t\)，接下來利用式（4.14）計算邊緣分布。

最後，為了確定最可能的狀態序列\(\mathbf{y}^*=\arg \max_{\mathbf{y}}p(\mathbf{y}|\mathbf{x})\)，我們將式（4.3）中所有的求和換為求最大值。於是，很容易理解，在式（4.3）中利用的技巧依舊有效。這就是維特比叠代。類假於前向變量\(\alpha\)，定義
\[ \delta_t(j) \overset{\text{def}}{=} \underset{\mathbf{y}_{\langle 1\dots t-1\rangle}}{\max} \Psi_t(j, y_{t-1}, x_t) \prod _{t‘=1}^{t-1} \Psi_{t‘}(y_{t‘}, y_{t‘-1},x_{t‘}). \tag{4.15} \]
同樣，也可以采用叠代方法計算
\[ \delta_t(j) =\max_{i\in S} \Psi_t(j,i,x_t) \delta_{t-1}(i). \tag{4.16} \]
一旦所有的\(\delta\)都計算完畢，最可能的狀態序列通過回溯來確定
\[ \begin{align} y_T^* &=\arg \max_{i\in S} \delta_T(i) \y_t^* &=\arg \max_{i \in S} \Psi_t(y_{t+1}^*, i, x_{t+1}) \delta_t(i) \qquad \text{for} \ t < T \end{align} \]
\(\delta_t\)和\(y_t^*\)的叠代過程，稱為__維特比算法__。

前向-後向算法和維特比算法可以直接推廣至線性鏈條件隨機場，與HMM基本一致，僅轉移權重\(\Psi_t(j,i,x_t)\)的定義不同。式（2.18）的條件隨機場可寫為：
\[ p(\mathbf{y}|\mathbf{x})=\frac{1}{Z(\mathbf{x})} \prod_{t=1}^T \Psi_t(y_t,y_{t-1},\mathbf{x}_t), \tag{4.17} \]
其中，
\[ \Psi_t(y_t,y_{t-1},\mathbf{x}_t) =\exp \left\{ \sum_k \theta_k f_k(y_t,y_{t-1}, \mathbf{x}_t)\right\}. \tag{4.18} \]
利用該定義，前向叠代（4.6）、後代叠代（4.9），以及維特比叠代（4.16）可以不加改變直接用於線性鏈條件隨機場。只是其含義解釋起來稍有區別。在條件隨機場中，\(\alpha_t(j)=p(\mathbf{x}_{\langle 1\dots t \rangle}, y_t=j)\)不再有HMM中那樣的概率解釋。需要從因子分解的角度來定義變量\(\alpha\)、\(\beta\)和\(\delta\)，即式（4.5）、式（4.8）和式（4.15）。此外，前向-後向叠代中的\(p(\mathbf{x})\)需替換為\(Z(\mathbf{x})\)，即\(Z(\mathbf{x})=\beta_0(y_0)\)， \(Z(\mathbf{x})=\sum_{i \in S} \alpha_T(i)\) 。

對於邊緣分布，將式（4.14）中的\(p(\mathbf{x})\)替換為\(Z(\mathbf{x})\)依舊成立
\[ \begin{align} p(y_{t-1},y_t|\mathbf{x})&=\frac{1}{Z({\mathbf{x})}} \alpha_{t-1}(y_{t-1}) \Psi_t(y_t,y_{t-1},\mathbf{x}_t) \beta_t(y_t). \tag{4.19} \p(y_t|\mathbf{x}) &= \frac{1}{Z(\mathbf{x})} \alpha_t(y_t) \beta_t(y_t). \tag{4.20} \end{align} \]
另外還有三個特殊的推斷任務也可以通過直接推廣HMM的算法完成。第一，從後驗概率\(p(\mathbf{y}|\mathbf{x})\)中獨立對\(\mathbf{y}\)取樣，可以利用前向算法與後向取樣相結合，與HMM完全一樣。第二，找到前\(k\)個最可能的序列而不僅是可能性最大的序列\(\arg \max_{\mathbf{y}} p(\mathbf{y}|\mathbf{x})\)，也可以利用HMM的算法[129]。第三，有時候需要計算下標為\(S \subset [1,2,\dots, T]\)的節點集合（可能不連續）上的邊緣概率\(p(\mathbf{y}_S|\mathbf{x})\)。例如，要度量模型根據輸入片段預測相應標記的信度。該邊緣概率可以直接利用前向後向相結合的方法高效計算，詳細內容參見Culotta和McCallum[30]。

4.2 圖模型上的推斷

對於任意結構圖模型，有多種精確推斷算法。盡管這些算法在最差情況下計算量是指數級的，但是在實際應用中大部分情況下還是比較有效的。最著名的精確算法是連接樹算法（junction tree algorithm），它不斷將變量分組直到圖變成一顆樹。一旦構建好一個等價樹，其邊緣分布即可使用針對樹的精確算法來計算。不過，對某些復雜的圖，連接樹算法會需形成很大的簇，這也是最壞情況下其計算量為指數級的原因。精確推斷的詳細內容參見Koller和Friedman[57]。

由於精確推斷的比較復雜，因此很多研究關註近似推斷算法。其中有兩類近似推斷算法獲得了比較多的關註：蒙特卡羅算法（Monte Carlo Algorithms）和__變分算法__（Variational Algorithms）。蒙特卡羅算法是一種隨機算法，它試圖從目標分布中近似地生成樣本。變分算法通過尋找一個與復雜邊緣分布非常接近的較簡單的近似分布，將推斷問題轉換成一個尋找該近似分布的優化問題。一般情況下，蒙特卡羅法在取樣時間足夠長的情況下是無偏的。而變分算法盡管速度要快得多，但卻是有偏的。原因是近似過程中產生的固有的誤差源，而且其影響也很難通過增加計算時間降低。盡管如此，變分算法對條件隨機場來說非常有用，因為參數估計過程中要求大量運行推斷算法，快速推斷過程對高效的訓練至關重要。關於MCMC（馬爾可夫鏈蒙特卡羅）的詳細內容請參考Robert和Casella[116]，關於變分方法請參考Wainwright和Jordan[150]。

本部分內容不僅能用於條件隨機場，而且能用於任意可根據因子圖進行因子分解的分布，無論是聯合分布\(p(\mathbf{y})\)還是條件分布\(p(\mathbf{y}|\mathbf{x})\)（如條件隨機場）。為了強調這一點，同時簡化符號標記，在下面的分析中我們暫時忽略對\(\mathbf{x}\)的依賴，僅討論因子圖\(G=(V,F)\)對應的聯合分布\(p(\mathbf{y})\)的推斷，即
\[ p(\mathbf{y})=Z^{-1}\prod_{a\in F} \Psi_a(\mathbf{y}_a). \]
若要推廣至條件隨機場，僅需簡單地將上式中的\(\Psi_a(\mathbf{y}_a)\)替換為\(\Psi_a(\mathbf{y}_a,\mathbf{x}_a)\)，並且將\(Z\)和\(p(\mathbf{y})\)修改為依賴於\(\mathbf{x}\)的條件概率形式。這種改變不僅從符號表示上有效，而且在實現設計上也是行得通的。推斷算法可以實現為能夠處理一般因子圖的形式，推斷過程不用關心它所處理的是無向的聯合分布\(p(\mathbf{y})\)、條件隨機場\(p(\mathbf{y}|\mathbf{x})\)，乃至有向圖模型。

本節其余的部分中給出兩個近似算法：蒙特卡羅算法和變分算法。關於近似算法有非常多的研究，由於空間所限不能在這裏一一介紹。相反，我們的目的是突出條件隨機場近似算法的共性問題。本節我們僅關註於推斷算法本身，第5部分將會討論它們在條件隨機場中的應用。

4.2.1 馬爾可夫鏈蒙特卡羅

目前，復雜模型中最常用的蒙特卡羅法是馬爾可夫鏈蒙特卡羅（Markov Chain Monte Carlo, MCMC）[116]。MCMC並不直接估計邊緣分布\(p(y_s)\)，而是從聯合分布\(p(\mathbf{y})\)中生成近似樣本。MCMC方法的核心是要構建一個馬爾可夫鏈，其狀態空間與\(Y\)相同。當該馬爾可夫鏈仿真運行的時間足夠長時，其狀態的分布接近\(p(y_s)\)。假設我們要近似求得函數\(f(\mathbf{y})\)在分布\(p(\mathbf{y})\)上的期望。給定MCMC方法中馬爾可夫鏈的采樣\(\mathbf{y}^1, \mathbf{y}^2, \dots, \mathbf{y}^M\)，可以通過下式近似求得該期望：
\[ \sum_{\mathbf{y}}p(\mathbf{y})f(\mathbf{y}) \approx \frac{1}{M}\sum_{j=1}^M f(\mathbf{y}^j). \tag{4.21} \]
在第5部分中，我們會使用這種方法在CRF訓練過程中計算期望值。

吉布斯采樣是MCMC方法的一種。在算法的每次叠代中，樣本的每個變量都在保持其他變量不變的情況下獨立地重新采樣。假設在第\(j\)次叠代中得到的樣本為\(\mathbf{y}^j\)。接下來生成下一個樣本\(\mathbf{y}^{j+1}\)，

• （1）令\(\mathbf{y}^{j+1} \leftarrow \mathbf{y}^j\).
• （2）對於每個\(s\in V\)，對\(Y_s\)重新采樣。從分布\(p(y_s|\mathbf{y}_{\backslash s},\mathbf{x})\)中采樣得到\(\mathbf{y}_s^{j+1}\).
• （3）返回結果\(\mathbf{y}_s^{j+1}\)。

註意，\(\mathbf{y}_{\backslash s}\)為\(\mathbf{y}\)中除\(y_s\)之外其余所有分量所構成的向量。而在2.1.1節中，求和符號\(\sum_{\mathbf{y}\backslash y_s}\)的含義是，對變量\(Y_s\)的值等於\(y_s\)的所有\(\mathbf{y}\)求和，註意不要混淆。

上述采樣過程定義了一個馬爾可夫鏈，可以用於近似求解式（4.21）的期望。在一般因子圖中，條件概率由下式計算
\[ p(y_s|\mathbf{y}_{\backslash s}) = \kappa \prod_{a\in F}\Psi_a(\mathbf{y}_a), \tag{4.22} \]
其中，\(\kappa\)為歸一化常量。（在下文中，\(\kappa\)表示一般歸一化常量，它在不同式子中形式可能不同）。式（4.22）中歸一化常量\(\kappa\)的計算要比聯合分布\(p(\mathbf{y}|\mathbf{x})\)中要容易得多，因為計算\(\kappa\)僅需對所有\(y_s\)的可能取值求和，而不必對整個向量\(\mathbf{y}\)求和。

吉布斯采樣主要的優點是實現簡單。實際上，像BUGS這樣的軟件包就可以輸入一個圖模型自動地生成相應的吉布斯采樣[78]樣本。它的主要缺點，是\(p(\mathbf{y})\)中有強依賴關系的情況下性能較差，而序列數據正是這種情況。這裏，“性能較差”是指馬爾可夫鏈需要叠代很多次才能到達穩定的分布\(p(\mathbf{y})\)。

關於MCMC算法的文獻很多。Robert和Casella[116]的書對其進行了綜述。然而，MCMC算法在條件隨機場中使用不多。或許是因為我們在前邊提到的缺點。在利用極大似然估計法進行參數估計時，邊緣分布計算的進行次數很多。最直接的情況下，梯度下降算法過程中訪問的每個參數配置中的每個訓練實例都需要運行MCMC算法。由於MCMC鏈需要數千次叠代才能收斂，以致於計算量大到無法接受。不過，也有辦法解決這個問題，比如不必要求MCMC鏈一直運行到收斂（參見5.4.3節）。

4.2.2 信念傳播

本部分介紹一種重要的變分推斷算法——信念傳播（Belief Propagation, BP）算法。BP算法是線性鏈條件隨機場中精確推斷算法的直接推廣，這點很有意思。

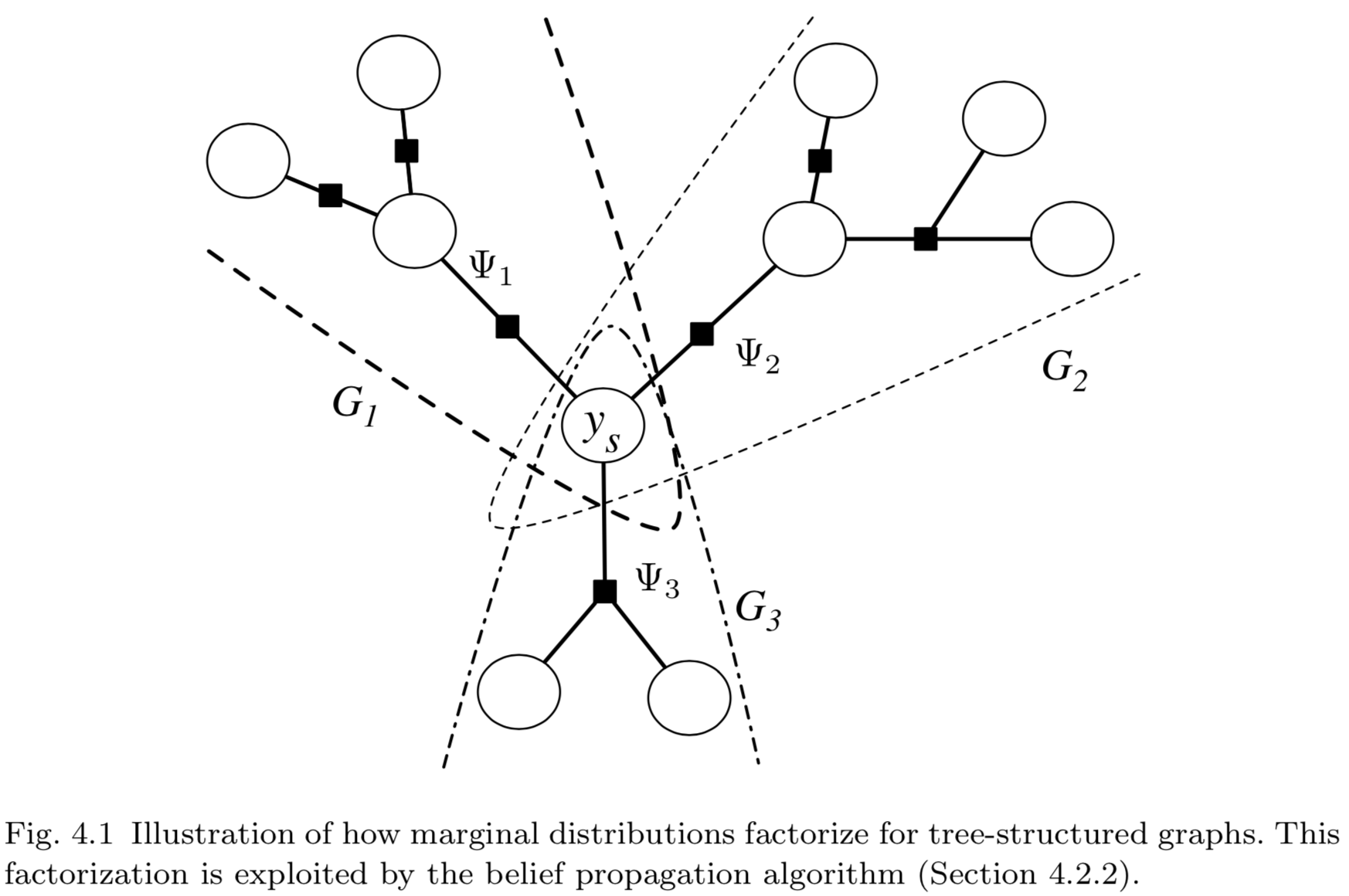
假設因子圖\(G=(V,F)\)是樹狀結構的，需要計算其中的變量\(Y_s\)的邊緣分布。BP算法的思想是，\(Y_s\)相鄰的因子以__消息__（message）乘積的形式對其邊緣分布產生作用。由於因子圖為樹狀結構，因此每個消息都可以獨立地計算。更正式地，對於每個下標為\(a \in N(s)\)的因子，記\(G_a=(V_a,F_a)\)為包含\(Y_s\)、\(\Psi_a\)以及\(G\)中\(\Psi_a\)的全部上遊節點（upstream）所組成的子圖。這裏，上遊節點（upstream）的含義是\(V_a\)包含了被\(\Psi_a\)從\(Y_s\)分割下來的所有節點，\(F_a\)則包含了被\(\Psi_a\)從\(Y_s\)分割下來的所有因子，如圖4.1所示。由於\(G\)是樹狀結構的，因此所有集合\(V_a \backslash Y_s \ \big(a\in N(s)\big)\)之間沒有交集，因子集合\(F_a\)之間同樣也沒有交集。這意味著，可以將求解邊緣分布的求和運算分解為多個獨立子問題之積：
\[ \begin{align} p(y_s) & \propto \sum_{\mathbf{y}\backslash y_s} \prod_{a\in F} \Psi_a(\mathbf{y}_a) \tag{4.23} \&= \sum_{\mathbf{y}\backslash y_s} \prod_{a\in N(s)} \prod_{\Psi_b \in F_a} \Psi_b(\mathbf{y}_b) \tag{4.24} \&= \prod_{a\in N(s)} \sum_{\mathbf{y}_{V_a} \backslash y_s} \prod_{\Psi_b \in F_a} \Psi_b(\mathbf{y}_b) \tag{4.25} \end{align} \]

註意：上式中，求和符號都是為了求相應變量\(Y_s\)的邊緣分布。其核心思想是，將各待求和部分的公因子提取到求和符號之外。

盡管式中的符號沒有明確標出，但要註意變量\(y_s\)包含在所有的\(y_a\)中，式（4.25）的兩側都包含了\(y_s\)。

將式（4.25）中的每個成分記為\(m_{as}\)，
\[ m_{as}(y_s)=\sum_{\mathbf{y}_{V_a}\backslash y_s} \prod_{\Psi_b\in F_a} \Psi_b(\mathbf{y}_b). \tag{4.26} \]
每個\(m_{as}\)只是變量\(y_s\)在子圖\(G_a\)中的邊緣分布。在整個圖\(G\)中，變量\(y_s\)的邊緣分布為所有子圖中邊緣分布的乘積。我們可以將每個\(m_{as}(y_s)\)比喻為因子\(a\)發給變量\(Y_s\)的消息（message），該消息反應了\(a\)的上遊（變量和因子）對變量\(Y_s\)邊緣分布的影響。類似地，我們可也可以將變量發送至因子的消息定義為
\[ m_{sa}(y_s)=\sum_{\mathbf{y}_{V_s}} \prod_{\Psi_b\in F_s} \Psi_b(\mathbf{y}_b). \tag{4.27} \]
於是，根據式（4.25），可知邊緣分布\(p(y_s)\)與\(Y_s\)接收到的消息之積成正比。類似地，因子的邊緣分布為
\[ p(\mathbf{y}_a) \propto \Phi_a(\mathbf{y}_a) \prod_{s\in N(a)}m_{sa}(\mathbf{y}_a). \tag{4.28} \]
若僅根據式（4.26）計算網絡中的消息是不可行的，因為還需要對所有的\(y_{V_a}\)求和，而\(V_a\)也可能非常大。幸運地，消息可以通過對局部求和進行叠代遞歸的方式計算。叠代公式為
\[ \begin{align} m_{as}(y_s)&=\sum_{\mathbf{y}_a \backslash y_s} \Psi_a(\mathbf{y}_a)\prod_{t\in a \backslash s}m_{ta}(y_t)\m_{sa}(y_s)&=\prod_{b\in N(s)\backslash a} m_{bs}(y_s). \end{align} \tag{4.29} \]
通過不斷的重復替換可看出，這個遞歸過程與\(m\)的顯式定義一致，可以用歸納法來證明。在樹狀網絡中，通過合理的安排，首先從根結點開始發送消息，將前項消息的計算總是放在依賴於它們的消息計算之前。這就是信念傳播算法[103]。

除了計算單個變量的邊緣分布，有時候我們還需要計算因子的邊緣分布\(p(\mathbf{y}_a)\)，以及給定取值\(\mathbf{y}\)的聯合概率\(p(\mathbf{y})\)。（回想前文所述，後者的計算很困難，因為要計算配分函數\(\log Z\)）。首先，為了計算因子的邊緣分布，我們可以利用與單變量邊緣分布同樣的分解方法，可得到
\[ p(\mathbf{y}_a)=\kappa \Psi_a(\mathbf{y}_a)\prod_{s\in N(a)} m_{sa}(y_s), \tag{4.30} \]
其中\(\kappa\)為歸一化常數。實際上，可以利用類似的方法計算任意相連接的變量集（可能不屬於同一因子）的邊緣分布。不過如果變量集合過大，對\(\kappa\)的計算依舊會非常困難。

BP也可以用於計算規範化常量\(Z\)。可以直接利用傳播算法，以一種4.1節介紹的前向-後向算法的擴展的形式進行。另一方法僅從算法最終得到的近似邊緣分布中計算\(Z\)。在樹狀結構的分布\(p(\mathbf{y})\)中，聯合分布可分解為
\[ p(\mathbf{y})=\prod_{s\in V}p(y_s) \prod_a \frac{p(\mathbf{y}_a)}{ \prod_{t\in a} p(y_t) }. \tag{4.31} \]

上式按圖4.1展開，或者將圖4.1中各節點和因子編號代入上式，即可明白

在線性鏈結構中
\[ p(\mathbf{y})=\prod_{t=1}^T p(y_t)\prod_{t=1}^T\frac{p(y_t,y_{t-1})}{p(y_t)p(y_{t-1})}, \tag{4.32} \]
上式通過調整，即為我們熟悉的形式\(p(\mathbf{y})=\prod_t p(y_t|y_{t-1})\)。利用這個特點，可以根據每個變量和每個因子的邊緣分布，計算任意取值下的\(p(\mathbf{y})\)。同時也求得\(Z=p(\mathbf{y})^{-1} \prod_{a\in F}\Psi_a (\mathbf{y}_a)\)。

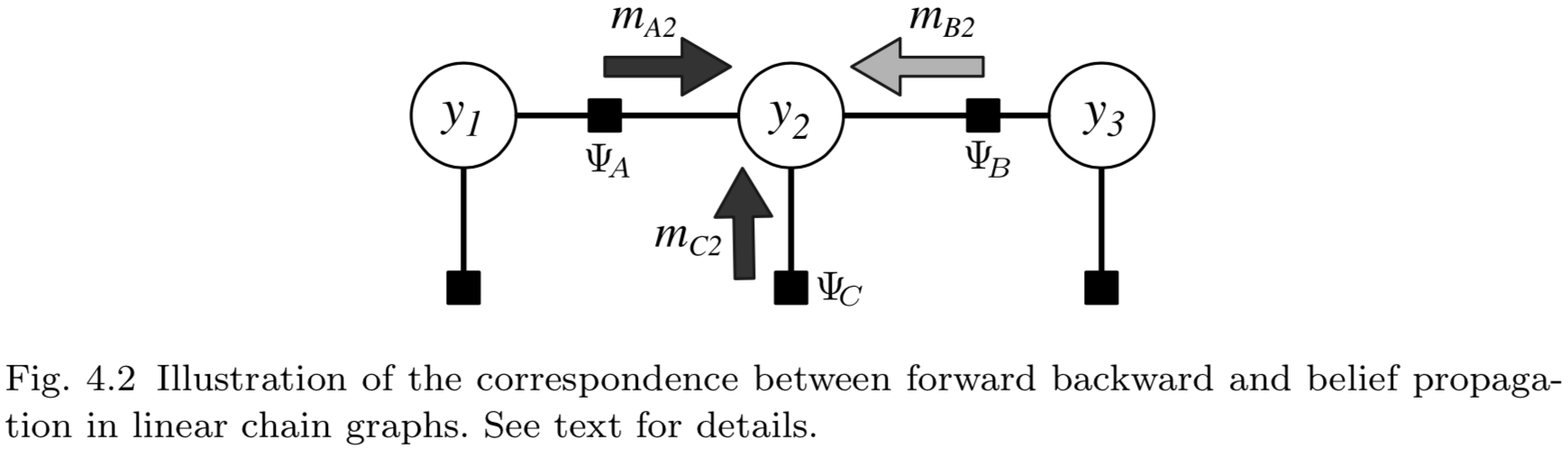
如果圖\(G\)是樹狀結構的，信念傳播算法能夠精確的計算邊緣分布。實際上，若\(G\)是一個線性鏈，BP算法退化為前向-後向算法（4.1節）。要理解這點，參考圖4.2。該圖是三節點線性鏈上BP消息的傳遞。為了看出其與前向-後向算法的一致性，4.1節中定義的前向變量\(\alpha_2\)等價於消息\(m_{A2}\)與\(m_{C2}\)之積（圖中的深灰色箭頭）。後向變量\(\beta_2\)等價於消息\(m_{B2}\)（淺灰色箭頭）。實際上，邊緣分布\(p(\mathbf{y}_a)\)的分解（式4.30）是線性鏈情況下（式4.14）的擴展。

若\(G\)不是樹狀結構，式（4.29）的消息更新不能保證得到精確的邊緣分布，甚至連算法的收斂性也不能保證。但是，依舊可以通過叠代以達到一個固定點（a fixed point）。該過程稱為環路信念傳播（loopy belief propagation）算法。為了強調該過程的近似性本質，我們將環路信念傳播算法得到的近似邊緣分布稱為信念（beliefs）而不是邊緣分布，標記為\(q(y_s)\)。

另一個問題是，在消息更新的叠代過程中如何調度計算順序。在樹狀結構中，何意的調度都能收斂至正確的邊緣分布，但是網絡中存在環路的情況下不再如此：計算順序不但影響環路信念傳播算法的結果，而且還影響算法的收斂性。實際中表現良好的一種簡單的辦法是對消息更新進行隨機的叠代。例如，按隨機的順序計算每個因子，通過式（4.29）接收並發送消息。不過，文獻[35,135,152]提出了其他巧妙、有效的方法。

令人驚訝的是，環路BP可被看作是一種變分推斷方法。其含義是，存在一個關於信念的目標函數，BP叠代過程使得該目標函數實現近似最小化。下面我們對這種解釋進行簡要的介紹，更詳細的內容請參考[150,158]。

變分算法的一般思想為：

• （1）定義一個容易處理的近似分布族\(\mathcal{Q}\)，以及目標函數\(\mathcal{O}(q)\ (\text{for}\ q\in\mathcal{Q} )\)。其中的每個\(q\)，要麽是邊緣分布容易計算的分布（如樹狀結構的分布），要麽是一個近似邊緣分布集合。如果是後者，這些近似邊緣分布稱為偽邊緣分布（pseudomarginals），因為它們不必與任何\(\mathbf{y}\)上的邊緣分布相一致。目標函數\(\mathcal{O}\)衡量\(q\in \mathcal{Q}\)對\(p\)的近似程度。
• （2）找到“最接近”的近似\(q^*=\min_{q\in \mathcal{Q}}\mathcal{O}(q)\)。
• （3）利用\(q^*\)作為邊緣分布\(p\)的近似。

例如，假設\(\mathcal{Q}\)為\(\mathbf{y}\)上所有可能分布的集合，目標函數為
\[ \begin{align} \mathcal{O}(q) &=\text{KL} (q||p) -\log Z \tag{4.33}\&= -H(q)-\sum_a \sum_{\mathbf{y}_a}q(\mathbf{y}_a)\log \Psi_a(\mathbf{y}_a), \tag{4.34} \end{align} \]
一旦通過最小化目標函數得到了\(q\)的最優解\(q^*\)，我們可以利用\(q^*\)的邊緣分布來近似\(p\)的邊緣分布。實際上，該變分問題在\(q^*=q\)時的最優值為\(\mathcal{O}(q^*)=-\log Z\)。因此，求解該變分公式等價於精確推斷。若要進行近似推斷，可以改變集合\(\mathcal{Q}\)（例如，要求\(q\)是完全因子分解的），或者對目標函數\(\mathcal{O}\)進行修改。例如，平均場方法添加了\(q\)完全因子分解的條件，即對特定\(q_s\)的選擇【簡單地講，將\(y_s\)根據因子分組】，有\(q(\mathbf{y})=\prod_s q_s(y_s)\)，然後找到使式（4.34）最小化的\(q\)。

下面，我們分析如何在變化法的背景下理解信念傳播算法。在變分推斷中需要做出兩種近似。第一種近似，是對式（4.34）中表示熵的項\(H(q)\)的近似，因為使用標準方法計算\(H(q)\)非常困難。如果\(q\)為樹狀結構的分布，熵可以精確的寫為
\[ H_{BETHE}(q)=-\sum_{a}\sum_{\mathbf{y}_a}q(\mathbf{y}_a)\log q(\mathbf{y}_a) + \sum_i \sum_{y_i}(d_i -1)q(y_i)\log q(y_i), \tag{4.35} \]
其中，\(d_i\)為\(i\)的度，也就是依賴於\(y_i\)的因子的數量。接下來，將式（4.31）所示的樹狀結構因子分解的聯合分布代入熵的定義之中。如果\(q\)不是樹，我們依舊將\(H_{\text{BETHE}}\)作為\(H\)的近似來計算變分目標函數\(\mathcal{O}\)。於是得到Bethe自由能（Bethe free energy）：
\[ \mathcal{O}_\text{BETHE}(q)=-H_\text{BETHE}(q)-\sum_a\sum_{\mathbf{y}_a}q(\mathbf{y}_a)\log\Psi_a(\mathbf{y}_a) \tag{4.36} \]
目標函數\(\mathcal{O}_\text{BETHE}(q)\)僅通過其邊緣分布依賴於\(q\)，因此我們可以在所有邊緣向量的空間上優化，而不是在整個概率分布\(q\)上優化。具體地，每個分布\(q\)有一個對應的信念向量（belief vector）\(\mathbf{q}\)，其元素為\(q_{a;y_a}\)（所有的因子\(a\)和變量取值\(y_a\)）和\(q_{i;y_i}\)（所有變量\(i\)及取值\(y_i\)）。所有可能信念向量的空間稱為邊緣多胞形（marginal polytope）[150]。不過，對於難以處理的模型，邊緣多胞形具有極其復雜的結構。這就引出了第二種利用環路BP的近似，即目標函數\(\mathcal{O}_\text{BETHE}\)在一個放松了的邊緣多胞形上進行優化。這種放松要求信念僅需局部一致（locally consistent），即
\[ \sum_{\mathbf{y}_a \backslash y_i } q_a(\mathbf{y}_a)=q_i(y_i) \ \ \forall a,i \in a. \tag{4.37} \]
作為一個技術點（technial point），如果一個假定的邊緣分布集滿足式（4.37），並不意味著它們是全局一致的，也就是說存在單一聯合分布\(q(\mathbf{y})\)滿足這些邊緣分布。由於同樣的原因，分布\(q_a(\mathbf{y}_a)\)也稱為偽邊緣分布。

Yedidia等[157]的研究表明，約束（4.37）下\(\mathcal{O}_\text{BETHE}\)的受限靜止點是環路BP的固定點。因此，我們也可以將Bethe能\(\mathcal{O}_\text{BETHE}\)看作環路BP的固定點所要優化的目標函數。

變分角度的解釋與從消息傳遞的角度解釋相比，有著更深理解深度。從中得到的要點之一是，它展示了如何利用環路BP來近似\(\log Z\)。因為我們將\(\min_q\mathcal{Q}_\text{BETHE}(q)\)作為\(\min_q\mathcal{O}(q)\)的近似，而且已知\(\min_q\mathcal{O}(q)=\log Z\)，因此定義\(\log Z_\text{BETHE}=\min_q\mathcal{O}_\text{BETHE}(q)\)為\(\log Z\)的近似看來是合理的。這在5.4.2節中討論利用BP估計條件隨機場參數時很重要。

4.3 實現問題

本節討論條件隨機場實現過程中的兩個重要技術問題：稀疏性和數值下溢。

第一，通常可以利用模型中的稀疏性提高推斷的效率。主要涉及到兩種類型的稀疏性：因子取值的稀疏性和特征的稀疏性。首先討論因子取值，回憶在線性鏈情況下，每個前向更新（式4.6）和向後更新（式4.9）的計算時間復雜度為\(O(M^2)\)，\(M\)為標記的數量。類似地，在任意結構條隨機場中，環路BP中一對因子的更新時間復雜度也為\(O(M^2)\)。然而，在某些模型中可以更有效的進行推斷，原因在於並非所有\((y_t,y_{t-1})\)上的因子都有取值，或者說因子\(\Psi_t(y_t,y_{t+1,\mathbf{x}_t})\)的取值常常是0。這種情況下，消息傳遞算法中可以利用稀疏矩陣運算大大降低計算量。

特征向量上取值的稀疏性也能達到提高遠算效率的目的。回憶式（2.26），計算因子\(\Psi_c(\mathbf{x}_c, \mathbf{y}_c)\)的過程中需要計算參數向量\(\theta_p\)和特征向量\(\mathbf{f}_c=\{f_{pk}(y_c, \mathbf{x}_c)| \forall p, \forall k\}\)的點積。而向量\(\mathbf{f}_c\)中的取值常常為0。例如，自然語言應用中常使用二值特征標識一個詞。這種情況下，因子\(\Psi_c\)的計算量可以利用稀疏向量大大的降低。同樣，我們也可以利用稀疏性提高似然梯度（likelihood gradient）的計算效率，如第5部分所示。

相關的另一個提高前向後向計算效率的技巧，是將特定轉移子集的參數綁定[24]。其作用是降低模型轉移矩陣的有效大小，從而降低對標記集大小的二次依賴性（quadratic dependence）。

第二個推斷算法實現的問題是如何避免數值下溢。前向-後向算法和信念傳播算法中的概率，即\(\alpha_t\)和\(m_{sa}\)，取值常常非常之小，以至於計算機中數值精度不能表示（在HMM中\(\alpha_t\)會隨時間\(t\)以指數速度向0減小）。有兩種標準的方法來解決這個問題。一種方法是將向量\(\alpha_t\)的求和有及向量\(\beta_t\)的求和調整至1（歸一化），使較小的值放大。這種調整不會影響\(Z(\mathbf{x})\)的計算，因為\(Z(\mathbf{x})=p(\mathbf{y}‘|\mathbf{x}‘)^{-1}\prod_t\big(\Psi_t(y_t‘,y_{t+1}‘,\mathbf{x}_t) \big)\)（對任意\(\mathbf{y}‘\)），其中\(p(\mathbf{y}‘|\mathbf{x})^{-1}\)利用式（4.31）基於邊緣分布計算。不過，Rabiner[111]提出了一種更有效的方法，該方法涉及到保存每個局部標度因子。在任何情況下，標度技巧都可被用於前向-後向算法或環路BP算法，並且不會影響最終的結果。

另一種避免數值下溢的方法是在對數域計算，即式（4.6）的前向叠代變為
\[ \log \alpha_t(j)=\bigoplus_{i\in S} \big( \log \Psi_t(j,i,x_t) + \log \alpha_{t-1}(i)\big), \tag{4.38} \]
其中\(\oplus\)的運算\(a \oplus b = \log(e^a +e^b)\)。最初看不出這種方法的作用，因為數值精度在計算\(e^a\)和\(e^b\)時丟失了。但\(\oplus\)可用下式計算
\[ a \oplus b = a + \log(1+ e^{b-a}) = b + \log(1+e^{a-b}), \tag{4.39} \]
如果我們用較小的指數來選取恒等式的話，上式的數值穩定會更好。

初看起來歸一化方法要優於對數方法，原因在於後者中\(\log\)和\(\exp\)的計算量達到\(O(TM^2)\)，這帶來了很大的計算開銷。這種情況在HMM中的確如此，但是在條件隨機場中並非如此。在條件隨機場中，即便是歸一化方法依舊要求調用\(\exp\)函數來計算式（4.18）的\(\Psi_t(y_t,y_{t+1},\mathbf{x}_t)\)。因此無法避免對指數函數的調用。在最壞的情況下，\(\Psi_t\)的計算次數達\(TM^2\)，與歸一化方法對指數的調用次數類似。不過，有些特殊情況下，歸一化方法可以帶來速度的提升，例如當轉移特征不依賴觀測時，僅有\(M^2\)個不同的\(\Psi_t\)取值。

條件隨機場介紹（4）—— An Introduction to Conditional Random Fields