前言

其實這是一個很玄學的算法，我也不是很懂。但是慢慢地寫，就慢慢地懂了。

例子

我們先看到這樣一個例子：
現有n個男生和n個女生，每一個女生對於一個男生都有一個期望值。現在想知道期望值最大是多少。

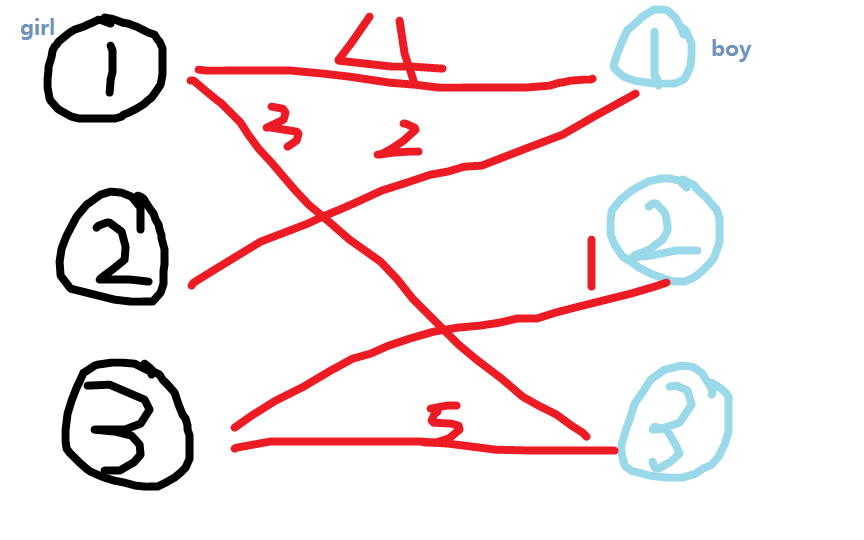
算法

那麽顯然,我們需要一種算法來完成這個任務,KM騰空出世!

在此之前,我們需要了解一些東西:

前置知識

期望值：女生連的邊中邊權最大的值，稱之為女生的期望值

l(x)+l(y)>=w(i,j)

當l(x)+l(y)=w(i,j)時，是M圖的完美匹配！

過程

原則

• 能換就換(思想很像匈牙利求二分圖最大匹配)

做法

1. 對於每一個妹子,選擇她最喜歡的男生
2. 如果無法達到以上要求,前往4
3. 如果可以,遞歸修改她人男友.前往1
4. 所有訪問過的女生值域減去
5. 訪問過的男生值域加上

代碼實現

復雜度及優化

以上代碼的復雜度為O(n^4)

有一些優化可以使代碼復雜度降為O(n^3)，由EK提出

顯然，每一次修改，我們都不停地在計算l(x)+l(y)-w(x,y)，不妨設一個變量slack表示l(x)+l(y)-w(x,y)，那麽顯然，我們每一次查詢就從O(n^2)變成了O(n)，每一次修改的復雜度為O(1)

例題

KM算法(二分圖完美匹配)