二分圖最大匹配：

問題描述：給出一個二分圖，找一個邊數最大的匹配。就是選擇儘量多的邊，使得選中的邊中任意兩條邊均沒有公共點。如果所有的點都是匹配點那就是一個完美匹配。

解決方案：增廣路定理

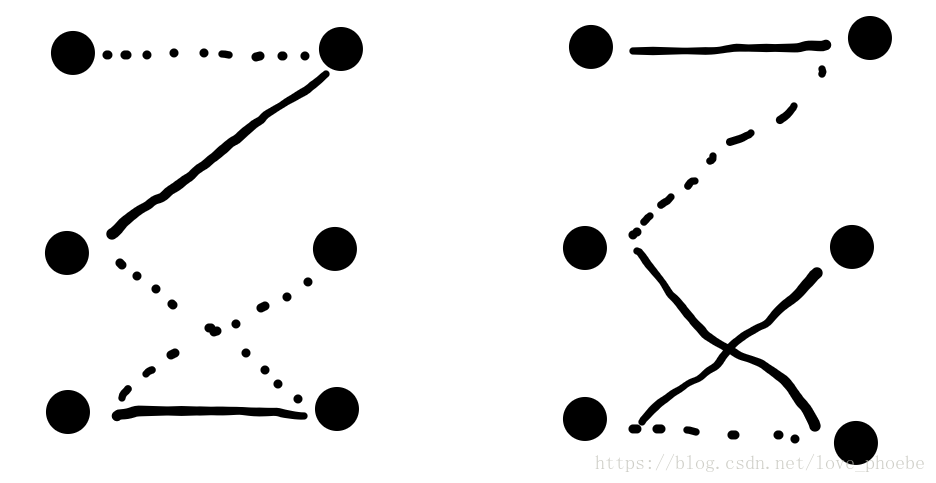
增廣路：從一個未匹配的點開始，依次走過未匹配邊，匹配邊，未匹配邊，匹配邊，。。。。。。 如果最後的終點是一個未匹配點（即最後一條邊是一條未匹配邊），那麼這條路就是一條增廣路。而將增廣路上的未匹配邊和匹配邊進行互換，就會使得匹配邊多一條，如圖：

由此可知，存在一條增廣路就可以將匹配的邊數加一。那麼一個匹配是最大匹配的充要條件便是不存在增廣路。此定理不僅僅適用於二分圖。

經典例子：n*m 的棋盤上放著一些棋子，要求保留最多的棋子使得任意兩枚棋子都不在同一行或者同一列。這時候可以將二分圖的左圖表示每一行，右圖表示每一列。棋盤（x,y）位置有棋子則表示左圖中代表x行的點與右圖中代表y列的點有一條邊相連。若兩條邊同時依賴於同一點則表示兩個棋子在同一行或者同一列，最多的棋子數就是最大匹配數。

關於最大匹配數的一些結論：

1，最大匹配數 = 最小頂點覆蓋（選取最少的點，使得點集中的點能覆蓋所有的邊） 

證明：首先要明確的一點是最小頂點覆蓋一定不會小於最大匹配數。顯而易見，最大匹配中的每一個匹配都是不相鄰的一條邊，如果最大匹配數為n，那麼至少需要n個頂點來覆蓋這n條邊。

剩下的證明相等，學習時看了許多部落格，怎麼形容呢，一頭霧水，no picture you say a jb？ 

兩種情況：

2，頂點數 - 最小頂點覆蓋 = 最小邊覆蓋 （邊最少的情況下，邊集中的邊覆蓋所有的點）

證明：設頂點數為 n ，最大匹配為 a。因為要使得邊最少，所以先選擇最大匹配的邊（一次可以覆蓋兩個點） ，剩下的每個點都需要一條邊去覆蓋，設剩下的為 b = n -2 * a  。而最小邊覆蓋此時等於 a + b =n - a，證完。

3，頂點數 = 最大匹配 + 最大獨立集 （點集，其中的點互不相連）

證明：頂點中去除最大匹配的點剩下的就是孤立的點，就是最大獨立集

匈牙利演算法（二分圖最大匹配演算法）

給出模板及例題 poj3041

題意：在網格上給出一些點，每次可以清除一行或一列的點，清除次數最少的情況下清除所有的點。用第一個結論最小頂點覆蓋 = 最大匹配數。

/*zhizhaozhuo 匈牙利演算法模板 && poj3041*/
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=1e3;
int Map[maxn][maxn],vis[maxn],pre[maxn];
void init(){
	memset(Map,0,sizeof(Map));
	memset(pre,0,sizeof(pre));
}
bool find(int x,int m){
	int i,j;
	for(int i=1;i<=m;i++){  //遍歷右圖 
		if(Map[x][i] && !vis[i]){ //x->i 有邊且 i 未被訪問 
			vis[i]=1;
			if(pre[i]==0 || find(pre[i],m)){ //i 未匹配且 通過 i 結點可以找到增廣路 
				pre[i]=x;
				return true;
			}
		}
	}
	return false;
}
int solve(int n,int m){
	int sum=0;
	for(int i=1;i<=n;i++){  //遍歷左圖 
		memset(vis,0,sizeof(vis));//清空標記 
		if(find(i,m))sum++;  
	}
	return sum;
}
int main(){
	int n,k;
	scanf("%d%d",&n,&k);
	init();
	while(k--){
		int a,b;
		scanf("%d%d",&a,&b);
		Map[a][b]=1;
	}
	int ans=solve(n,n);
	printf("%d\n",ans);
	return 0;
}
 

二分圖最大權匹配：

前面所說的最大匹配可以看做是權值均為1的最大權匹配，最大權匹配就是帶權的最大匹配。

原理及證明：

完備（美）匹配：二分圖中左右子圖中的各點都有對應的匹配。

KM演算法是通過給每一個點一個頂標來把求最大權匹配的問題轉換為求完備匹配的問題。

設左圖的頂標為A[i] ,右圖的頂標為B[j] ,頂點之間的邊權為 w[i] [j]。可行性頂標 A[i] +B[j] >= w(i,j)，即頂標始終滿足對於任意的一條邊，它連線的兩個頂點的頂標和大於等於該邊的邊權，初始時左圖中點的頂標等於與該點相連的邊中邊權最大的值，右圖中點的頂標等於0.而將最大權匹配轉換為完備匹配的關鍵定理就是：若由二分圖中所有滿足A[i] +b[j]=w[i][j] 的邊<i,j> 構成的子圖(也稱相等子圖) 有完備匹配，那麼這個完備匹配就是二分圖的最大權匹配。 因為完備匹配中的邊都是等於兩端點的頂標和的，而根據之前對頂標的定義可知非完備匹配中的邊小於等於兩端點的頂標和。

如果當前的子圖中不存在完備匹配，就修改頂標的值再求完備匹配。

頂標的修改方法：在增廣路徑（交錯樹）上的左圖集合中的點 i 減去一個值alter ，右圖集合中的點 j 加上alter。

分為四種情況：1，i，j都屬於增廣路，A[i] - alter + B[j] + alter =w(i,j) 邊的可行性不變，即原來是相等子圖的邊現在仍是，不是仍不是。

                         2，i屬於增廣路，j不屬於增廣路，A[i] - alter + B[j] ,值就變小了，那麼此時這條不屬於相等子圖的邊（屬於早就被 j 遍歷到了）就有可能加入到相等子圖中。

                         3，如果i不屬於增廣路，j屬於增廣路，A[i] + B[j] +alter ,值變大了，這條不屬於相等子圖的邊就更不可能加入了。

                          4，i，j都不屬於增廣路則不對其進行任何操作，可行性不變。

修改量alter的取值：因為修改頂標是為了將邊加入構成相等子圖，所以可以看出是選擇上面的第二種情況。而且要滿足

A[i] +B[j] >= w(i,j)    即：     A[i] - alter + B[j] >= w(i,j)   即：alter >= A[i] +B[j] - w(i,j) 即 alter =min（ A[i] +B[j] - w(i,j) ）

（注意此時要求i屬於增廣路，j不屬於增廣路  ）

模板及例題： Hdu-2255，直接套就行

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=1e3,INF=1e9;

int W[maxn][maxn],n;
int Lx[maxn],Ly[maxn];//頂標 
int Left[maxn];//右邊第i個點對應的左邊的點的編號 
bool S[maxn],T[maxn];//是否在增廣路 

bool match(int i){
	S[i]=true;
	for(int j=1;j<=n;j++)if(Lx[i]+Ly[j]==W[i][j] && !T[j]){//i到j可行 且 j未被訪問 
		T[j]=true;
		if(!Left[j] || match(Left[j])){ //j未標記 或者 通過j可以找打增廣路 
			Left[j]=i;return true;
		}
	}
	return false;
}
void update(){//更新頂標 
	int a=INF;
	for(int i=1;i<=n;i++)if(S[i]){
		for(int j=1;j<=n;j++)if(!T[j])a=min(a,Lx[i]+Ly[j]-W[i][j]);//i在增廣路 且 j不在增廣路中 
	}
	for(int i=1;i<=n;i++){
		if(S[i])Lx[i]-=a;
		if(T[i])Ly[i]+=a;
	}
}
void KM(){
	for(int i=1;i<=n;i++){
		Left[i]=Lx[i]=Ly[i]=0;
		for(int j=1;j<=n;j++)Lx[i]=max(Lx[i],W[i][j]);
	}
	for(int i=1;i<=n;i++){
		for(;;){
			for(int j=1;j<=n;j++)S[j]=T[j]=0;
			if(match(i))break;else update();
		}
	}
}

int main(){
	while(~scanf("%d",&n)){
		for(int i=1;i<=n;i++){
		    for(int j=1;j<=n;j++)scanf("%d",&W[i][j]);
	    }
	    KM();
	    int sum=0;
	    for(int i=1;i<=n;i++)sum+=W[Left[i]][i];
		printf("%d\n",sum);
	}
	return 0;
}