題目地址：

https://leetcode.com/problems/longest-palindromic-substring/description/

題目：

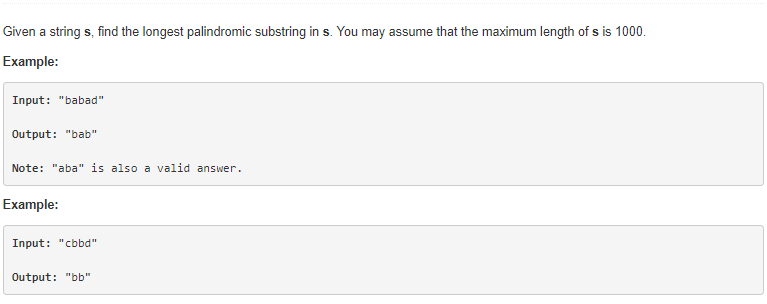
其實就是求一個字符串的最長回文子字符串。

解法：

我首先采取了暴力解法，不出意料地TLE了。這是超時的TLE解法：

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() == 0) return "";
        string str;
        string longest;
        int max = 0
 
;
        for (int i = 0; i < s.size(); i++) {
            str = "";
            for (int j = i; j < s.size(); j++) {
                str += s[j];
                if (isPalindrome(str) && str.size() > max) {
                    longest = str;
                    max = str.size();
                }
            }
        }
        
 
return longest;
    }
    bool isPalindrome(string s) {
        for (int i = 0; i < s.size() / 2; i++) {
            if (s[i] != s[s.size() - i - 1]) return false;
        }
        return true;
    }
};

這類題目一看就是用動態規劃解決的問題。我們可以使用一個二維布爾數組dp[i][j]來表示字符串s從i到j這個子字符串是否一個子字符串。

它的狀態轉移方程是這樣的：

i == j ：dp[i][j] = true

j - i == 1：if (s[i] == s[j]) dp[i][j] = true

else dp[i][j] = false

j - i >= 1: if (s[i] == s[j] && dp[i + 1][j - 1]) dp[i][j] = true

else dp[i][j] = false

由於遞推的時候dp[i][j]需要看dp[i + 1][j - 1]的值，因此要註意循環中i和j的變化順序。

代碼如下：

class Solution {
public:
    string longestPalindrome(string s) {
        bool ispalindrome[s.size()][s.size()] = {false};
        int left, right, len = -1;
        for (int i = s.size(); i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (i == j) ispalindrome[i][j] = true;
                else if (j - i == 1) ispalindrome[i][j] = s[i] == s[j] ? true : false;
                else ispalindrome[i][j] = (s[i] == s[j] && ispalindrome[i + 1][j - 1]) ? true : false;
                if (ispalindrome[i][j] && j - i + 1 > len) {
                    len = j - i + 1;
                    left = i;
                    right = j;
                }
            }
        }
        return s.substr(left, right - left + 1);
    }
};

[LeetCode] 5 Longest Palindromic Substring