卡特蘭數相關問題
一、什麽是Catalan數
說到Catalan數，就不得不提及Catalan序列，Catalan序列是一個整數序列，其通項公式是
遞推公式是
C(n) = C(1)*C(n-1) + C(2)*C(n-2) + ... + C(n-1)C(1)，n>=2
我們從中取出的
就叫做第n個Catalan數，前幾個Catalan數如下：
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …
咋看之下沒什麽特別的，但是Catalan數卻是許多計數問題的最終形式。
二、Catalan數在組合計算中的應用
1、矩陣鏈乘：
P=a1×a2×a3×……×an，依據乘法結合律，不改變其順序，只用括號表示成對的乘積，有幾種括號化的方案？
2、一個棧(無窮大)的進棧序列為1，2，3，…，n，有多少個不同的出棧序列?
3、n個節點構成的二叉樹，共有多少種情形？
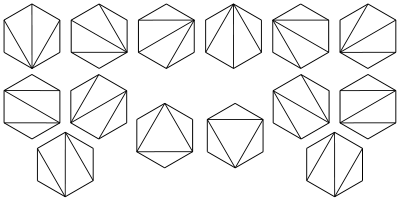
4、求一個凸多邊形區域劃分成三角形區域的方法數？
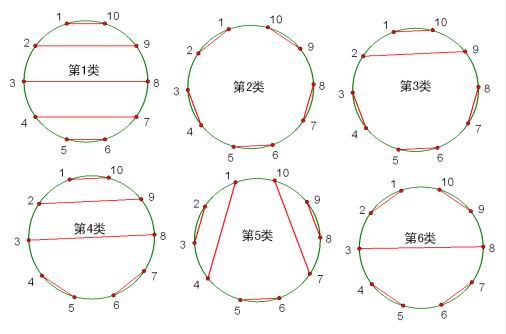
5、在圓上選擇2n個點，將這些點成對鏈接起來使得所得到的n條線段不相交，一共有多少種方法？(下圖供參考)
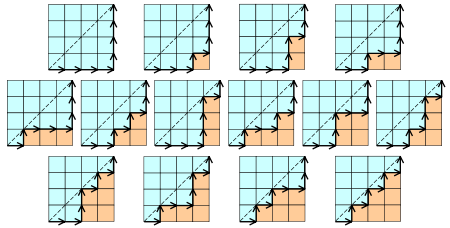
6、n*n的方格地圖中，從一個角到另外一個角，不跨越對角線的路徑數為h(n).例如，
4×4方格地圖中的路徑有：
7、n層的階梯切割為n個矩形的切法數也是。如下圖所示：
8、有2n個人排成一行進入劇場。入場費5元。其中只有n個人有一張5元鈔票，另外n人只有10元鈔票，劇院無其它鈔票，問有多少中方法使得只要有10元的人買票，售票處就有5元的鈔票找零？
9、甲乙兩人比賽乒乓球，最後結果為20∶20，問比賽過程中甲始終領先乙的計分情形的種數。
10、2n個高矮不同的人，排成兩排，每排必須是從矮到高排列，而且第二排比對應的第一排的人高，問排列方式有多少種？
以上題目的最終解均與卡特蘭數相關，具體的求解分析見“參考資料”。
參考資料：
從《編程之美》買票找零問題說起，娓娓道來卡特蘭數——兼爬坑指南
卡特蘭數相關問題