在程式設計之美上又看到卡特蘭數的題目，所以就把這類題目做個總結。

至此，已經遇到過得卡特蘭數的題目有：

1、12個高矮不同的人，排成兩排，每排必須是從矮到高排列，而且第二排比對應的第一排的人高，問排列方式有多少種？

解答：12個高矮不同，則可以編號1 2 3 4 5 6 7 8 9 10 11 12 ，現在0代表第一排，1代表第二排 

000000111111是一個合法序列，010101010101也是一個合法序列，可以看到對於每個1，只要前面的0的個數大於等於1的個數就是一個合法序列，011000001111，由於第2個1，前面0只有1個，1有兩個，不符合。

換個角度，1號1的位置大於1號0的位置，2號1的位置大於2號0的位置。。。。，6號1的位置大於6號0的位置

2、用S表示入棧，X表示出棧，那麼合法的序列有多少個(S的個數為n)

解答：出棧X前必須要有大於等於X個數的S操作，SSSSXXXX合法，SXSXSXSX合法，但是SXXSSXSX就不合法，和上題一樣，1號X的位置要大於1號S的位置，2號X的位置要大於2號S的位置，以此類推

3、括號化問題。矩陣鏈乘： P=A1×A2×A3×……×An，依據乘法結合律，不改變其順序，只用括號表示成對的乘積，試問有幾種括號化的方案？

解答：每個右括號前面要有大於等於左括號的個數，和前面題目一樣，1號右括號位置大於1號左括號，2號右括號位置大於2號左括號。。。

4、假設有2N個人在排隊買票，其中有N個人手持50元的鈔票，另外有N個人手持100元的鈔票，假設開始售票時，售票處沒有零錢，問這2N個人有多少種排隊方式，不至使售票處出現找不開錢的局面？

解答：每個持100的前面必須要有大於等於持50的人的個數，即1號100必須在1號50右邊，2號100必須在2號50右邊。。。直到n號

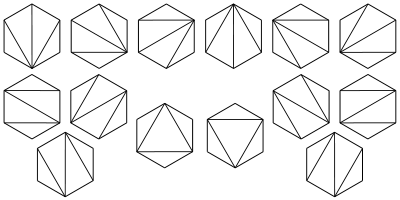
5、將多邊行劃分為三角形問題。將一個凸多邊形區域分成三角形區域(劃分線不交叉)的方法數?

類似：在圓上選擇2n個點,將這些點成對連線起來使得所得到的n條線段不相交的方法數?

6、給頂節點組成二叉樹的問題。
　　給定N個節點，能構成多少種形狀不同的二叉樹？

這六道題目看似不同，實則是一樣的， 即對每種合法排列來說，裡面的每個元素都必須滿足某個條件（常常是前面的某個個數要多於自己型別元素的個數）

     解答：(一定是二叉樹！先取一個點作為頂點，然後左邊依次可以取0至N-1個相對應的，右邊是N-1到0個，兩兩配對相乘，就是h(0)*h(n-1) + h(2)*h(n-2) + ...... + h(n-1)h(0)=h(n))   （能構成h（N）個）

卡特蘭數

原理：
令h(1)＝1,catalan數滿足遞迴式：
h(n)= h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1) (其中n>=2)
另類遞迴式：
h(n)=((4*n-6)/(n))*h(n-1);
該遞推關係的解為：
h(n)=C(2n,n)/(n + 1) (n=1,2,3,...)

talk is cheap，show the code：

#include <iostream>
using namespace std;

int bit_cnt(int n)//計算非負整數中二進位制數中1的個數
{
	int result = 0;
	for (; n; n &= n-1, ++result);
	return result;
}

int main(void)
{
	int F[6], B[6];//F代表前排 B代表後排
	int i,j,k,state,ok,ans = 0;
	for (state = 0; state < (1 << 12); ++state)
	{
		if (bit_cnt(state) == 6)
		{
			i = j = 0;
			for (int k = 0; k < 12; ++k)//確定每個0和1所在的位置
			{
				if(state&(1<<k))
					F[i++] = k;
				else
					B[j++] = k;
			}
			ok = 1;
			for (k = 0; k < 6; ++k)//篩選滿足條件的排列
			{
				if (B[k] < F[k])
				{
					ok = 0;
					break;
				}
			}
			ans += ok;
		}
	}
	cout << ans << endl;
	return 0;
}