頻分復用(Frequency Division Multiplexer)
作者:桂。
時間:2017年12月19日20:43:04
鏈接:http://www.cnblogs.com/xingshansi/p/8067839.html
前言
主要記錄基本的頻分復用原理,以及仿真實現。
一、頻分復用原理
頻分復用FDM:
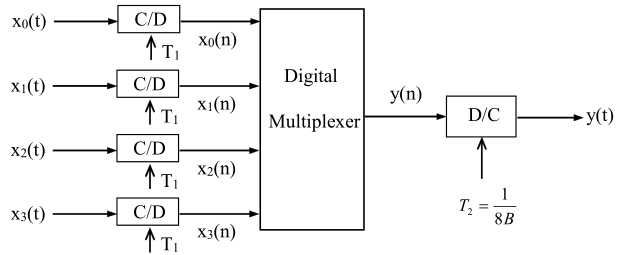
通常x1..4(t)可以是同一個序列的串並轉化,也可以是不同序列,頻分復用示意圖:
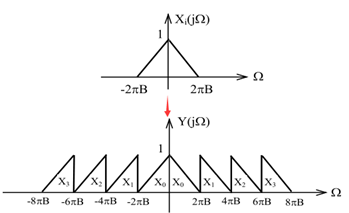
主要包含三個操作:1)上采樣(up-sample); 2)濾波(fir);3)累加(sum)。
頻分復用:將多個不同頻段的信號拼接為一個寬帶信號,主要包含三個操作:1)上采樣(up-sample); 2)濾波(fir);3)累加(sum)。
- 上采樣
T1/T2 = 4,故上采樣倍數為4,上采樣有原數據保持、插值、補零等方法,這裏采用最基本的補零方法。不失一般性,X0(n)、X1(n)、X2(n)、X3(n)分別按不同頻率的正弦信號處理。
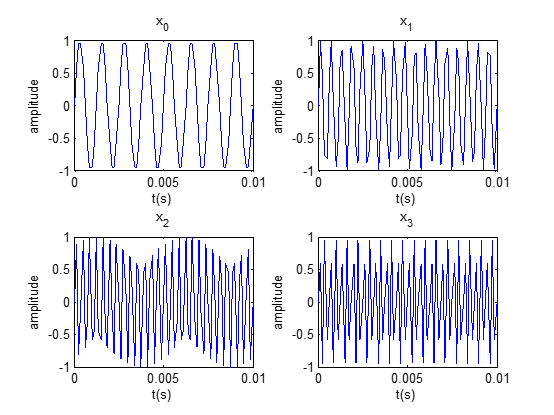
以x1(n) 的頻域變換:
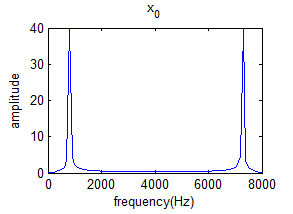
4倍插值後的頻譜:
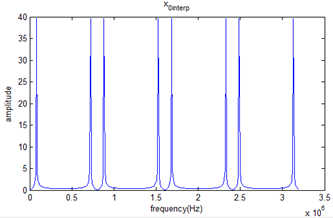
可以看出插值後出現了多個重復周期,因此需要借助低通濾波以保留單一周期,如下圖所示:
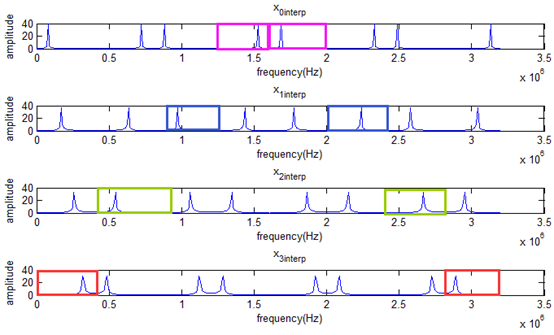
因此需要構造不同頻段的濾波器,四個藍色陰影部分拼接(累加)即可。
- 濾波器
這裏prototype濾波器:
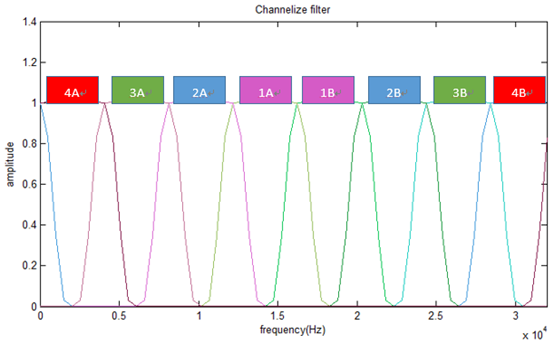
共構造8個濾波器,分成四組,輸出y(n)為:
Y(n) = y0(n)+ y1(n)+ y2(n)+ y3(n)
ym
Ym(n) = xm_interpl(n)*[ha (n) exp((-im*2*pi*(m*n))/8)+ ha(n) exp((-im*2*pi*((8-m)*n))/8)]
= 2*xm_interpl(n)*[ha(n)cos((-2*pi*(m*n))/8)]
其中ha (n) = h(n)* exp((-im*pi*n)/8)為prototype filter,至此便完成了信號的頻分多路復用(FDM)理論推導.
- 累加
濾波後的各個輸出累加,即得到調制的y(n),仿真圖如圖所示:
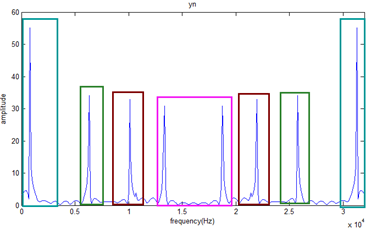
結果與上文一致。
二、仿真結果
頻分復用的接收端是發射的逆過程,分別利用 基本濾波器、多相濾波器實現:
基本濾波器:
%recovery signal: x
clc;clear all;close all;
load fir2.mat;
fir = fir2;
B = 4000;%4KHz
fs1 = 2*B;
D = 4;
t1 = 0:1/fs1:(128-1)/fs1;
f = [800 1600 2200 2800];%frequency
x0 = sin(2*pi*t1*f(1));
x1 = sin(2*pi*t1*f(2));
x2 = sin(2*pi*t1*f(3));
x3 = sin(2*pi*t1*f(4));
x_shape = [x0;x1;x2;x3];
%% interp
x0_interp = [x0;zeros(3,length(t1))];
x0_interp = x0_interp(:)‘;
x1_interp = [x1;zeros(3,length(t1))];
x1_interp = x1_interp(:)‘;
x2_interp = [x2;zeros(3,length(t1))];
x2_interp = x2_interp(:)‘;
x3_interp = [x3;zeros(3,length(t1))];
x3_interp = x3_interp(:)‘;
%%prototype filter
x_all = [x0_interp;x1_interp;x2_interp;x3_interp;flipud([x0_interp;x1_interp;x2_interp;x3_interp])];
im = sqrt(-1);
iseq = 1:length(fir);
for j = 1:D
h_channel(j,:) = fir.*cos((2*pi*((j-1/2)*(iseq-1)))/8);
% h_channel(j,:) = fir.*exp((1j*2*pi*((j-1/2)*(iseq-1)))/8);
end
%%add signal
yn = zeros(1,length(x3_interp));
for i = 1:D
yn = filter(h_channel(i,:),1,x_all(i,:))+yn;
end
%%demultiplex
x_channel = zeros(D,length(yn)/D);
for i = 1:D
x_channel(i,:) = downsample(filter(h_channel(i,:),1,yn),D);
end
figure()
for i = 1:D
subplot(2,2,i)
plot(linspace(0,fs1,length(t1)),abs(fft(x_channel(i,:))));
xlabel(‘frequency(Hz)‘);ylabel(‘amplitude‘);title(‘direct filter -> x‘);
end
%%plot mse
figure()
for i = 1:4
x_channel(i,:) = x_channel(i,:)/max(abs( x_channel(i,:)));
subplot (2,2,i)
plot(linspace(0,fs1,length(t1)),x_channel(i,:));hold on;
plot(linspace(0,fs1,length(t1)),x_shape(i,:),‘r--‘);hold on;
% plot(linspace(0,fs1,length(t1)),abs(x_shape(i,:)-x_channel(i,:)).^2,‘k‘);
xlabel(‘frequency(Hz)‘);title(‘MSE‘);
% legend(‘recovery‘,‘orignal‘,‘MSE‘);
end
多相濾波器,推導:
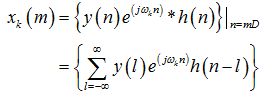
令l = iD+p,D表示分解後信號路數,此處D = 4:
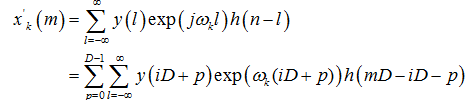
令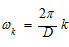 ,
,
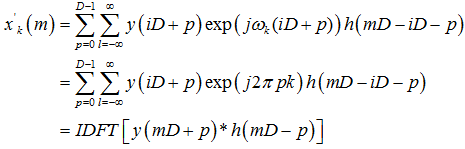
再將結果取實部即可得解。
%recovery signal by polyphase filter: x
clc;clear all;close all;
load fir2.mat;
fir = fir2;
B = 4000;%4KHz
fs1 = 2*B;
D = 4;
t1 = 0:1/fs1:(128-1)/fs1;
f = [800 1600 2200 2800];%frequency
x0 = sin(2*pi*t1*f(1));
x1 = sin(2*pi*t1*f(2));
x2 = sin(2*pi*t1*f(3));
x3 = sin(2*pi*t1*f(4));
x_shape = [x0;x1;x2;x3];
%% interp
x0_interp = [x0;zeros(3,length(t1))];
x0_interp = x0_interp(:)‘;
x1_interp = [x1;zeros(3,length(t1))];
x1_interp = x1_interp(:)‘;
x2_interp = [x2;zeros(3,length(t1))];
x2_interp = x2_interp(:)‘;
x3_interp = [x3;zeros(3,length(t1))];
x3_interp = x3_interp(:)‘;
%%prototype filter
x_all = [x0_interp;x1_interp;x2_interp;x3_interp;flipud([x0_interp;x1_interp;x2_interp;x3_interp])];
im = sqrt(-1);
iseq = 1:length(fir);
for j = 1:D
h_channel(j,:) = fir.*cos((-2*pi*((j-1/2)*(iseq-1)))/8);
% h_channel(j,:) = fir.*exp((1j*2*pi*((j-1/2)*(iseq-1)))/8);
end
%%add signal
yn = zeros(1,length(x3_interp));
for i = 1:D
yn = filter(h_channel(i,:),1,x_all(i,:))+yn;
end
%%demultiplex
%prototype filter
h0 = fir.*exp((-1j*2*pi*((-1/2)*(iseq-1)))/8);
h_py = fliplr(reshape(h0,D,length(h0)/D));
y_py = (reshape(yn,D,length(yn)/D));
x_channel = zeros(D,length(yn)/D);
for i = 1:D
x_channel(i,:) = filter(h_py(i,:),1,y_py(i,:));
end
x_channel = real(ifft(x_channel));
x_channel = x_channel([1,4,2,3],:);
%%plot mse
figure()
for i = 1:4
x_channel(i,:) = x_channel(i,:)/max(abs( x_channel(i,:)));
subplot (2,2,i)
plot(linspace(0,fs1,length(t1)),x_channel(i,:));hold on;
plot(linspace(0,fs1,length(t1)),x_shape(i,:),‘r--‘);hold on;
% plot(linspace(0,fs1,length(t1)),abs(x_shape(i,:)-x_channel(i,:)).^2,‘k‘);
xlabel(‘frequency(Hz)‘);title(‘MSE‘);
% legend(‘recovery‘,‘orignal‘,‘MSE‘);
end
三、其他
原型濾波器信道化思路:
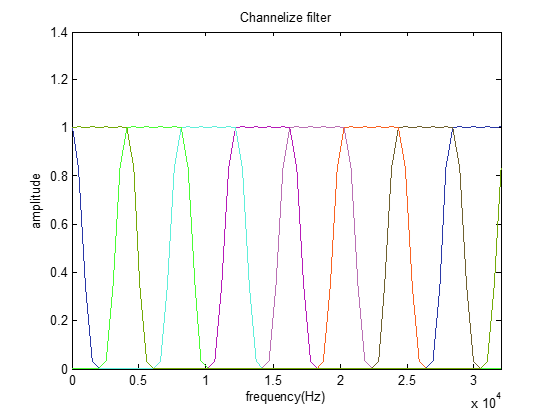
信道化與頻分復用略有不同,頻分復用主要是余弦函數,理論上相鄰無衰減,得到的余弦曲線並不理想:
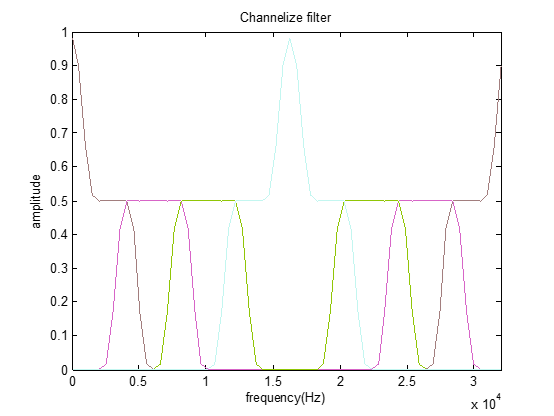
當有一定的過渡帶時,余弦曲線:
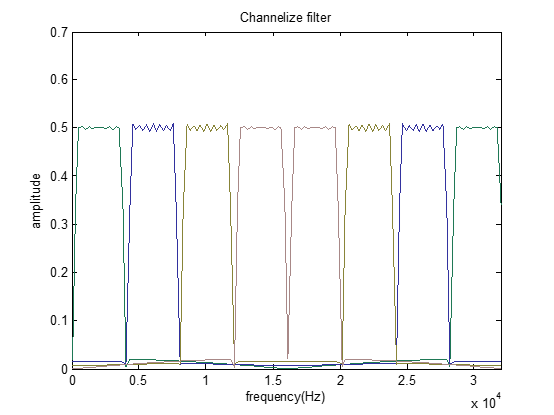
可見此時應該有一個過渡帶才更加合理,而不是像信道化體系常用的約束:相鄰信道無縫連接。
頻分復用(Frequency Division Multiplexer)
