算法之遞歸

阿新 • • 發佈：2017-12-22

第一次關系 href str cti 後來 dom ast 對象

什麽是遞歸？

百度百科：程序調用自身的編程技巧稱為遞歸（ recursion）。遞歸做為一種算法在程序設計語言中廣泛應用。一個過程或函數在其定義或說明中有直接或間接調用自身的一種方法，它通常把一個大型復雜的問題層層轉化為一個與原問題相似的規模較小的問題來求解，遞歸策略只需少量的程序就可描述出解題過程所需要的多次重復計算，大大地減少了程序的代碼量。遞歸的能力在於用有限的語句來定義對象的無限集合。一般來說，遞歸需要有邊界條件、遞歸前進段和遞歸返回段。當邊界條件不滿足時，遞歸前進；當邊界條件滿足時，遞歸返回。

一個比喻：知乎上的某位同行對遞歸覺得最恰當的比喻，就是查詞典。我們使用的詞典，本身就是遞歸，為了解釋一個詞，需要使用更多的詞。當你查一個詞，發現這個詞的解釋中某個詞仍然不懂，於是你開始查這第二個詞，可惜，第二個詞裏仍然有不懂的詞，於是查第三個詞，這樣查下去，直到有一個詞的解釋是你完全能看懂的，那麽遞歸走到了盡頭，然後你開始後退，逐個明白之前查過的每一個詞，最終，你明白了最開始那個詞的意思（來源——知乎李鵬

）

幾個小案例原地址 階乘的運算描述： n! = n*(n-1)*...2*1

function test(n){
    if(n <= 1){
        return 1;
    }else{
        return n*test(n-1);
    }
}
console.log(test(5));  //120

//下面使用arguments.callee來代替被遞歸的函數，
//目的是為了防止函數名的緊密耦合。同時簡化了代碼
function test(n){
    if(n <= 1) return 1;
    return n*arguments.callee(n-1);
}
console.log(test( 
5)); //120

斐波那契數列描述：斐波納契數列，又稱黃金分割數列，指的是這樣一個數列：1、1、2、3、5、8、13、21、……求第n個數是多少

function test(n){
    if(n <= 0) return 0;
    if(n <= 1) return 1;
    return arguments.callee(n-1) + arguments.callee(n-2);
}
console.log(test(6)); //8

走樓梯問題

描述：樓梯有n階臺階，上樓可以一步上1階，也可以一步上2階或者3階，計算共有多少種不同的走法。

function 
 test(n){
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 2;
    if(n == 3) return 4;
    return arguments.callee(n-1) + arguments.callee(n-2)+arguments.callee(n-3);
}
console.log(test(6)); //24


思路：
這其實就是一個斐波那契數列的一種實現。我們分析的時候，可以轉化成小規模的子類問題。
當到達指定階梯的最後一步的時候，可以有三種種情況，一是上一步，二是上兩步，三是上三步。
所以總的方法是F(n) = F(n-1) + F(n-2) + F(n-3)。然後自然就成了各自的小計算，不斷循環下去，直到判斷條件的發生。

最大公約數

描述：給兩個數，如果兩個數相等，最大公約數是其本身。如果不等，取兩個數相減的絕對值和兩個數中最小的數比較，相等則為最大公約數，不等則繼續上面的算法，直到相等。

function test(a,b){
    if(a == b) return a;
    return arguments.callee(Math.abs(a-b),Math.min(a,b));
}
console.log(test(15,12)); //3

漢諾塔

描述：百度百科

function test(n,src,aux,dest){
    if(n > 0){
        test(n-1,src,dest,aux);
        console.log("移動第"+n+"個圓盤從"+src+"到"+dest);
        test(n-1,aux,src,dest);
        }
}
console.log(test(3,"A","B","C")); 

思路：
在我沒有體會到遞歸的精粹前，我對這個問題簡直百思不得其解。我一直問自己，我怎麽知道下一個該去哪裏？
後來，我就知道，我其實更關心的是，最後那一個該怎麽走。這個怎麽說呢？我們可以從頭想起，我們如果只有1個盤，
我們可以讓它到C柱，也可以到B柱。自然兩個盤，也可以實現。3個盤，也是可以的吧。那我們就講4個盤的情況。
4個盤要完成就要將A上的圓盤，完全轉移到C上。我們把前3個盤當作一個整體放到B上，然後第4個盤就可以到C上了，
然後我們再將前三個放到C上，就成功了。那前三個盤，又可以重新當作一個新遊戲，讓前兩個盤，當一個整體，依次類推。
這樣我們只需要關心大的整體的事，其它的就轉成小規模問題解決就好了。

二分法快排

描述：使用二分法，對一個數組進行由小到大的排序。參考博客

<!DOCTYPE html>
<html>
  <head>
    <meta charset="UTF-8">
    <title></title>
  </head>
  <body>
    <script>
      function quickSort(arr) {
        if(arr.length <= 1) return arr;
        var leftArr = [];
        var rightArr = [];
        var pivot = Math.random(arr.length / 2);
        var baseNum = arr.splice(pivot, 1);

        arr.forEach(function(num) {
          if(num < baseNum) {
            leftArr.push(num);
          } else {
            rightArr.push(num);
          }
        });
        return quickSort(leftArr).concat(baseNum, quickSort(rightArr));
      }
      console.log(quickSort([1, 4, 5, 6, 2, 7, 13, 8, 9]));
    </script>
  </body>
</html>

DOM樹的遞歸描述：獲取一個節點的所有父節點的tagName

<!DOCTYPE html>
<html>
  <head>
    <meta charset="UTF-8">
    <title></title>
  </head>
  <body>
    <div id="box">
      <div id="content">
        <div id="last"></div>
      </div>
    </div>

    <script>
      var arr = [];
      var getParent = function(node) {
        node = node.parentNode;
        if(node.tagName) {
          arr.push(node.tagName);
          getParent(node);
        }
      }
      getParent(document.getElementById("last"));
      console.log(arr); //["DIV", "DIV", "BODY", "HTML"]
    </script>
  </body>
</html>

看了以上這麽多算法題，不知道各位老鐵掌握了多少。如果還是暈暈的，沒關系，接下來還有大量的習題加強理解。 1、一個遞歸算法必須包括（）？技術分享圖片

終止條件和遞歸部分

View Code 2、任何一個遞歸過程是否都可以轉換成非遞歸過程？技術分享圖片

正確
詳細討論地址：https://www.zhihu.com/question/20418254

View Code

3、給定下列程序，那麽執行的結果為多少？

function foo(x,y){
   if(x <= 0||y <= 0){
          return 1;
   }else{
          return 3*foo(x-6,y/2);
   }          
}
console.log(foo(20,13));

解析：
foo(20, 13) = 3 * foo(14, 6) = 3 * 3 * foo(8, 3) = 3 * 3 * 3 * foo(2, 1) = 3 * 3 * 3 * 3 * foo(-4, 0) =3 * 3 * 3 * 3 * 1 = 81

View Code

4、給定下列程序，那麽執行的結果為多少？

function f(x){
     if(x <= 2){
          return 1;
      }else{
          return f(x-2)+f(x-4)+1;
     }
}
console.log(f(10));

針對這樣的題目在別的地方看到的比較好的方法是用樹來表示
                                     10
                             8                  6
                       6         4        4       2
                   4     2    2  0    2   0
                2   0
圖中樹的節點數是15，所以是調用了15次

View Code

5、只有那種使用了局部變量的遞歸過程在轉換成非遞歸過程時才必須使用棧？

錯誤
解析：遞歸工作棧裏面包括返回地址、本層的局部變量和遞歸調用的形參代換用實參，所以正常情況下，無論遞歸過程有沒有使用局部變量，轉換為非遞歸過程都需要用棧來模擬這個遞歸調用過程

View Code

6、有一段樓梯臺階有15級臺階，以小明的腳力一步最多只能跨3級，請問小明登上這段樓梯有多少種不同的走法?

解析：請查看案例“走樓梯問題”

7、4個圓盤的Hanoi塔,總的移動次數為多少？

設f(n)為n個圓盤的hanoi塔總的移動次數，其遞推方程為f(n)=f(n-1)+1+ f(n-1)=2*f(n-1)+1。理解就是先把上面n-1個圓盤移到第二個柱子上(共f(n-1)步），再把最後一個圓盤移到第三個柱子(共1步），再把第二柱子上的圓盤移動到第三個柱子上（共f(n-1)步）。
而f（1）=1；於是f(2)=3,f(3)=7,f(4)=15。故答案為C。
進一步，根據遞推方程其實可以得出f(n) = 2^n - 1。

View Code

8、下列函數的執行結果為多少？

function f(i){
     if(i>1){
          return i*f(i-1);
    }else{
          return 1;
    }
}
console.log(f(5));

這裏展開如下：
f(5) = 5*f(4)
      = 5*4*f(3)
      = 5*4*3*f(2)
      = 5*4*3*2*f(1)
      = 5*4*3*2*1
      = 120

View Code

9、遞歸次數與各元素的初始排列有關。如果每一次劃分後分區比較平衡，則遞歸次數少；如果劃分後分區不平衡，則遞歸次數多。遞歸次數與處理順序無關。

10、n！後面有多少個0,6！=1*2*3*4*5*6=720.720後面有1個0，n=10000，求n！

10000/5=2000 有2000個能被5整除
2000/5=400     這2000個裏面能被5整除有400個（2000個已被5除過1次。能除第二次的有400）
400/5=80         同理 80個
80/5=16           同理 16個
16/5=3余1        同理 3個
結果2000+400+80+16+3=2499

View Code

11、對遞歸程序的優化的一般的手段是什麽？

尾遞歸優化

View Code

12、一個遞歸算法如下，那麽f(f(9))需要計算多少次f函數（註：這種題目，畫樹圖最直觀快速）

function f(i){
    if(i<=3){
          return 1;
    }else{
          return f(i-2)+f(i-6)+1;
   }
}

一、先算內層f(9)
    [1] 計算 f(9) = f(7) + f(3) + 1;
    [2] 計算[1]中 f(7) = f(5) + f(1) + 1;
    [3] 計算[2]中 f(5) = f(3) + f(-1) + 1;
    [4] 計算[3]中 f(3) = 1;
    [5] 計算[3]中 f(-1) = 1;
        {至此f(5)可計算得： f(5) = 1 + 1 + 1 = 3}
    [6] 計算(1)中f(1) = 1;
        {至此f(7)可計算得 ：f(7) = 3 + 1 + 1 = 5}
    [7] 計算[1]中f(3) = 1;
        {至此f(9)可計算得：f(9) = 5 + 1 + 1 = 7}
    計算f(9)一共調用了7次函數

二、計算外層f(7)
    由上面步驟可知，計算f(7)調用了5次函數
    所以一共調用了函數7+5=12次

View Code

13、遞歸函數最終會結束，那麽這個函數一定有一個分支不調用自身。 14、對n個記錄的線性表進行快速排序為減少算法的遞歸深度,每次分區後,先處理較短的部分。 15、當n=5時，下列函數的返回值是多少

function f(i){
    if(i<2){
          return i;
   }else{
          return f(i-1)+f(i-2);
   }
}
console.log(f(5));

解法一：
f(0)=0;
f(1)=1;
f(2)=f(1)+f(0)=1;
f(3)=f(2)+f(1)=2;
f(4)=f(3)+f(2)=3;
f(5)=f(4)+f(3)=5;

View Code

解法二：

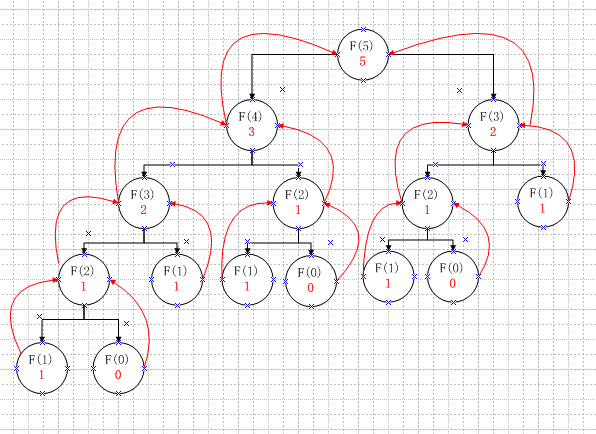
技術分享圖片

16、設有遞歸算法如下，那麽f(f(8))時需要計算多少次f函數？

function x(i){
   if(i<=3){
          return i;
   }else{
          return x(i-n)+x(i-4)+1;
   }
}

解法一：
x(8)=x(6)+x(4)+1  遞歸計算x(8)第一次調用
x(6)=x(4)+x(2)+1  遞歸計算x(6)第二次調用
x(4)= x(2)+x(0)+1  遞歸計算x(4)第三次調用
x(4)= x(2)+x(0)+1   遞歸計算x(4)第四次調用 
之後再調用x()計算黑體部分的結果(5次，加上前面4次，一共9次)，最後x(8)返回值為9

接著計算x(9)
x(9)=x(7)+x(5)+1  遞歸計算x(9)第一次調用
x(7)=x(5)+x(3)+1  遞歸計算x(7)第二次調用
x(5)=x(3)+x(1)+1  遞歸計算x(5)第三次調用
x(5)=x(3)+x(1)+1  遞歸計算x(5)第四次調用
之後再調用x()計算黑體部分的結果(5次，加上前面4次，一共9次)，最後x(8)返回值為9

解法二：
根據題意，易得x(3) = x(2) = x(1) = x(0) = 1
x(8) = x(6) +x(4) +1
       = x(4) + x(2) +1 + x(2) + x(0) +1 + 1 
       = x(2) + x(0) +1 + 1 + 1 +1 + 1 +1 + 1 
       = 9 
x(8)  這個就調用了9次函數x(int n)
同理可得x(9)也是調用了9次函數x(int n)
所以總共18次。

View Code

17、在遞歸算法執行過程中，計算機系統必定會用到的數據結構是棧 18、遞歸函數中的形參是自動變量

算法之遞歸

第一次關系 href str cti 後來 dom ast 對象什麽是遞歸？百度百科：程序調用自身的編程技巧稱為遞歸（ recursion）。遞歸做為一種算法在程序設計語言中廣泛應用。一個過程或函數在其定義或說明中有直接或間接調用自身的一種方法，它通常把一個大型復雜

算法之遞歸

算法之遞歸

算法學習——遞歸之排隊購票問題

算法學習——遞歸之快速排序

動態規劃和分治法，貪心算法以及遞歸的再一次深刻理解和體會

八大排序算法之七-歸並排序

【算法】遞歸

回溯法之遞歸回溯和迭代回溯

what' the python之遞歸函數與二分算法

基礎算法之三——遞歸法

遞歸算法之漢諾塔

《算法圖解》之遞歸

PHP開發之遞歸算法的三種實現方法

Java學習筆記——排序算法之進階排序（堆排序與分治並歸排序）

SparkMLlib學習分類算法之邏輯回歸算法

SparkMLlib回歸算法之決策樹

排序算法之歸並排序

算法之歸並排序

排序算法之歸並排序（Merge Sort）

從零開始學習算法之歸並排序[1]（2.2歸並排序）

day5-python之遞歸與二分法

算法之遞歸

相關推薦