前端學算法之算法復雜度
前面的話
本文將詳細介紹算法復雜度
大O表示法
大O表示法是描述算法的性能和復雜程度。 分析算法時,時常遇到以下幾類函數
符號 名稱 O(1) 常數的 O(log(n)) 對數的 O((log(n))c) 對數多項式的 O(n) 線性的 O(n2) 二次的 O(nc) 多項式的 O(cn) 指數的
如何衡量算法的效率?通常是用資源,例如CPU(時間)占用、內存占用、硬盤占用和網絡占用。當討論大O表示法時,一般考慮的是CPU(時間)占用
下面用一些例子來理解大O表示法的規則
【O(1)】
function increment(num){ return ++num; }
假設運行increment(1)函數,執行時間等於X。如果再用不同的參數(例如2)運行一次increment函數,執行時間依然是X。和參數無關,increment函數的性能都一樣。因此,我們說上述函數的復雜度是O(1)(常數)
【O(n)】
現在以順序搜索算法為例:
function sequentialSearch(array, item){ for (var i=0; i<array.length; i++){if (item === array[i]){ //{1} return i; } } return -1; }
如果將含10個元素的數組([1, ..., 10])傳遞給該函數,假如搜索1這個元素,那麽,第一次判斷時就能找到想要搜索的元素。在這裏我們假設每執行一次行{1} ,開銷是1。
現在,假如要搜索元素11。行{1}會執行10次(遍歷數組中所有的值,並且找不到要搜索的元素,因而結果返回 -1)。如果行{1}的開銷是1,那麽它執行10次的開銷就是10,10倍於第一種假設
現在,假如該數組有1000個元素([1, ..., 1000])。搜索1001的結果是行{1}執行了1000次(然後返回-1)
sequentialSearch函數執行的總開銷取決於數組元素的個數(數組大小),而且也和搜索的值有關。如果是查找數組中存在的值,行{1}會執行幾次呢?如果查找的是數組中不存在的值,那麽行{1}就會執行和數組大小一樣多次,這就是通常所說的最壞情況
最壞情況下,如果數組大小是10,開銷就是10;如果數組大小是1000,開銷就是1000。可以得出sequentialSearch函數的時間復雜度是O(n),n是(輸入)數組的大小
回到之前的例子,修改一下算法的實現,使之計算開銷:
function sequentialSearch(array, item){ var cost = 0; for (var i=0; i<array.length; i++){ cost++; if (item === array[i]){ //{1} return i; } } console.log(‘cost for sequentialSearch with input size ‘ + array.length + ‘ is ‘ + cost); return -1; }
用不同大小的輸入數組執行以上算法,可以看到不同的輸出
【O(n2)】
用冒泡排序做O(n2)的例子:
function swap(array, index1, index2){ var aux = array[index1]; array[index1] = array[index2]; array[index2] = aux; } function bubbleSort(array){ var length = array.length; for (var i=0; i<length; i++){ //{1} for (var j=0; j<length-1; j++ ){ //{2} if (array[j] > array[j+1]){ swap(array, j, j+1); } } } }
假設行{1}和行{2}的開銷分別是1。修改算法的實現使之計算開銷:
function bubbleSort(array){ var length = array.length; var cost = 0; for (var i=0; i<length; i++){ //{1} cost++; for (var j=0; j<length-1; j++ ){ //{2} cost++; if (array[j] > array[j+1]){ swap(array, j, j+1); } } } console.log(‘cost for bubbleSort with input size ‘ + length + ‘ is ‘ + cost); }
如果用大小為10的數組執行bubbleSort,開銷是100(102)。如果用大小為100的數組執 行bubbleSort,開銷就是10 000(1002)。需要註意,我們每次增加輸入的大小,執行都會越來越久
時間復雜度O(n)的代碼只有一層循環,而O(n2)的代碼有雙層嵌套循環。如 果算法有三層遍歷數組的嵌套循環,它的時間復雜度很可能就是O(n3)
時間復雜度
下圖比較了前述各個大O符號表示的時間復雜度:
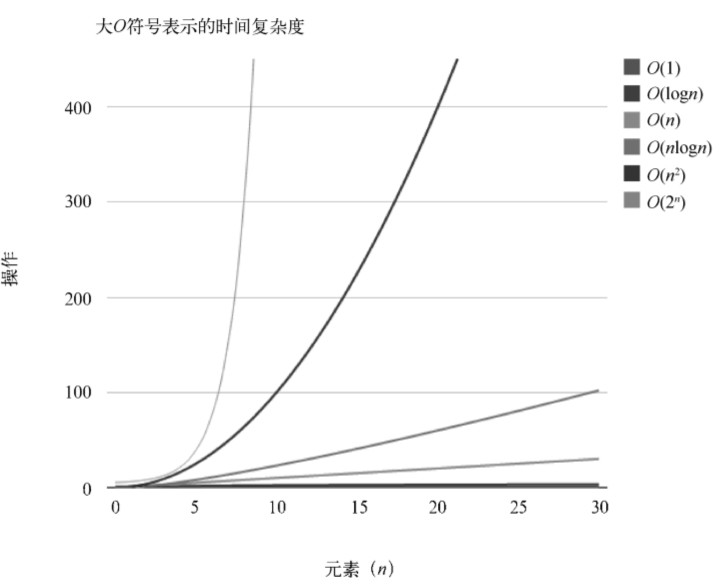
下表是常用數據結構的時間復雜度
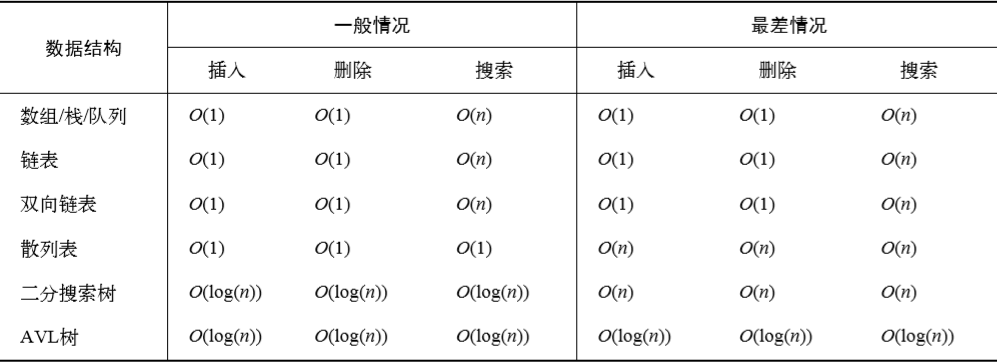
下表是圖的時間復雜度:

下表是排序算法的時間復雜度:
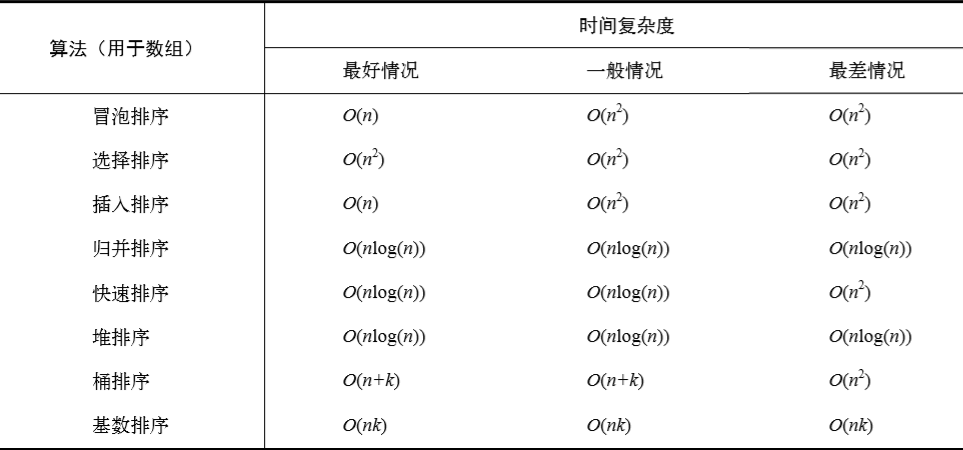
下表是搜索算法的時間復雜度:

NP
一般來說,如果一個算法的復雜度為O(nk),其中k是常數,我們就認為這個算法是高效的,這就是多項式算法
對於給定的問題,如果存在多項式算法,則計為P(polynomial,多項式)
還有一類NP(nondeterministicpolynomial,非確定性多項式)算法。如果一個問題可以在多項式時間內驗證解是否正確,則計為NP。如果一個問題存在多項式算法,自然可以在多項式時間內驗證其解。因此,所有的P都是NP。然而,P=NP是否成立,仍然不得而知。NP問題中最難的是NP完全問題,它滿足以下兩個條件:(1)是NP問題,也就是說,可以在多項式時間內驗證解,但還沒有找到多項式算法;(2)所有的NP問題都能在多項式時間內歸約為它。為了理解問題的歸約,考慮兩個決策問題L和M。假設算法A可以解決問題L,算法B可以驗證輸入y是否為M的解。目標是找到一個把L轉化為M的方法,使得算法B可以用於構造算法A
還有一類問題,只需滿足NP完全問題的第二個條件,稱為NP困難問題。因此,NP完全問題也是NP困難問題的子集
下面是滿足P < > NP時,P、NP、NP完全和NP困難問題的歐拉圖:
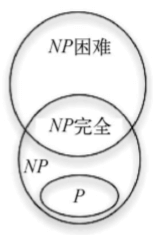
非NP完全的NP困難問題的例子有停機問題和布爾可滿足性問題(SAT)。 NP完全問題的例子有子集和問題、旅行商問題、頂點覆蓋問題等等
我們提到的有些問題是不可解的。然而,仍然有辦法在符合要求的時間內找到一個近似解。啟發式算法就是其中之一。啟發式算法得到的未必是最優解,但足夠解決問題了。啟發式算法的例子有局部搜索、遺傳算法、啟發式導航、機器學習等
前端學算法之算法復雜度
