八皇後問題(N皇後問題)
阿新 • • 發佈:2018-02-12
template 坐標 name pla std obj move 結構 cas 首先來看看這張模擬八皇後的圖。
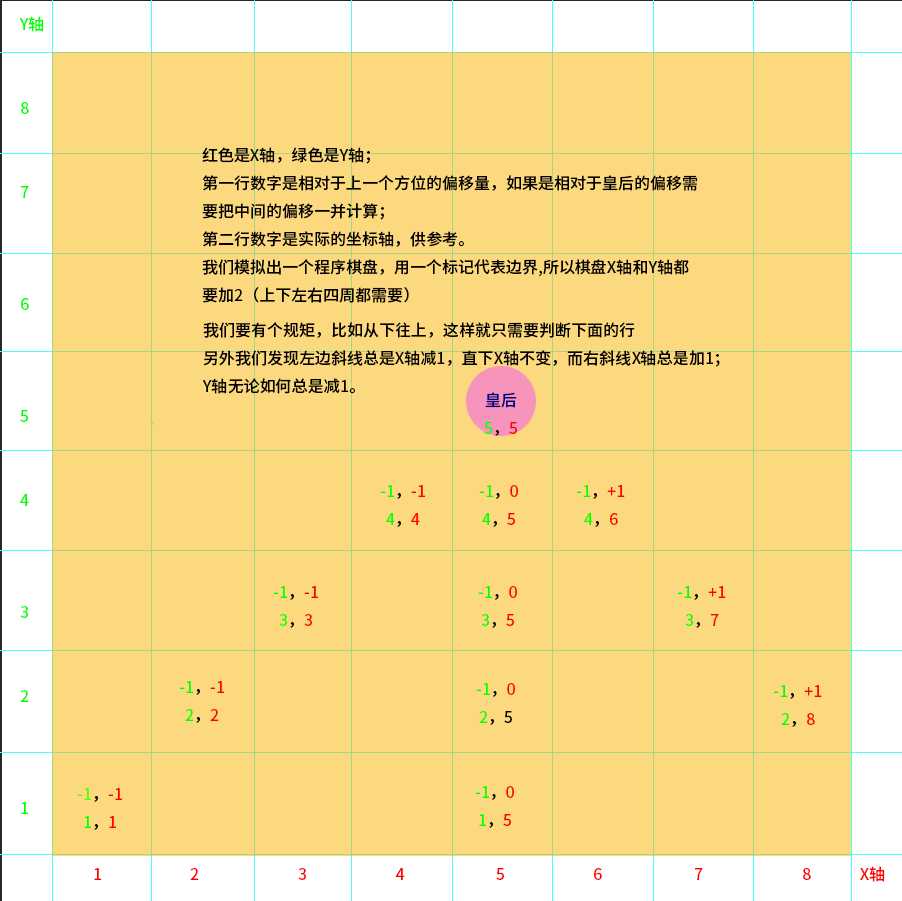 下面這張黑色背景是其中一個方案的截圖,第一行代表皇後的坐標;後面的是棋盤,其中*是邊界,空格是空區,#是皇後。
下面這張黑色背景是其中一個方案的截圖,第一行代表皇後的坐標;後面的是棋盤,其中*是邊界,空格是空區,#是皇後。
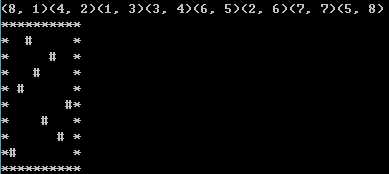
 下面這張黑色背景是其中一個方案的截圖,第一行代表皇後的坐標;後面的是棋盤,其中*是邊界,空格是空區,#是皇後。
下面這張黑色背景是其中一個方案的截圖,第一行代表皇後的坐標;後面的是棋盤,其中*是邊界,空格是空區,#是皇後。

#include <iostream> #include <cstring> #include "DTString.h" #include "LinkList.h" // 這裏使用鏈表存儲皇後位置 using namespace std; using namespace DTLib; template <int SIZE> // N皇後問題,SIZE表示皇後個數或者棋盤大小 class QueenSolution : publicObject { protected: enum { N = SIZE + 2 }; // 為了邊界識別,棋盤四周都要加一格 struct Pos : public Object // 方位結構體 { Pos(int px = 0, int py = 0) : x(px), y(py) { } int x; int y; }; int m_chessboard[N][N]; // 棋盤,0表示空位,1表示皇後,2表示邊界 Pos m_direction[3]; // 方向-1,-1表示左斜線;0,-1表示下方;1,-1表示右斜線;首先從最下方開始,所以只需考慮前面的行。LinkList<Pos> m_solution; // 用鏈表記錄解決方案 int m_count; // 記錄有效方案數量 void init() { m_count = 0; // 有效方案初始化為0 for(int i=0; i<N; i+=(N-1)) // 遍歷第0行和最後一行 { for(int j=0; j<N; j++) // 遍歷每一列 { m_chessboard[i][j]= 2; // 給棋盤的上下設置邊界 m_chessboard[j][i] = 2; // 給棋盤的左右設置邊界 } } for(int i=1; i<=SIZE; i++) // 初始化棋盤為空位 { for(int j=1; j<=SIZE; j++) { m_chessboard[i][j] = 0; } } m_direction[0].x = -1; // 初始化方向數據 m_direction[0].y = -1; m_direction[1].x = 0; m_direction[1].y = -1; m_direction[2].x = 1; m_direction[2].y = -1; } void print() // 打印有效方案,方案記錄了坐標值 { for(m_solution.move(0); !m_solution.end(); m_solution.next()) // 打印坐標 { cout << "(" << m_solution.current().x << ", " << m_solution.current().y << ")" ; } cout << endl; // 坐標打印換行 for(int i=0; i<N; i++) // 打印棋盤 { for(int j=0; j<N; j++) { switch(m_chessboard[i][j]) { case 0: cout << " "; break; // 空位 case 1: cout << "#"; break; // 皇後 case 2: cout << "*"; break; // 邊界 } } cout << endl; } cout << endl; // 棋盤打印完換行 } bool check(int x, int y, int d) // 檢查是否可放置皇後 { bool flag = true; do { x += m_direction[d].x; y += m_direction[d].y; flag = flag && (m_chessboard[x][y] == 0);// 查看坐標位置是否有空位 } while( flag ); // 本次循環後不會再有空位 return (m_chessboard[x][y] == 2); // 返回真就是到邊界,否則就是有皇後 } void run(int j) // 檢查當前行有沒有可放置皇後的位置 { if( j <= SIZE ) // 檢查當前行在棋盤內,註意不要跑到邊界上 { for(int i=1; i<=SIZE; i++) { if( check(i, j, 0) && check(i, j, 1) && check(i, j, 2) ) // 如果if為真表示可以放置皇後 { m_chessboard[i][j] = 1; // 標記該處有皇後 m_solution.insert(Pos(i, j)); // 記錄皇後的位置到鏈表 run(j + 1); // 遞歸判斷下一行 m_chessboard[i][j] = 0; // 回溯後要把棋盤當前位置的皇後清除,避免下一次調用時還有上次的皇後位置 m_solution.remove(m_solution.length() - 1); // 回溯後記錄皇後位置的鏈表長度也要減少 } } } else // 如果j大於SIZE就表示一輪檢查結束,方案計數加1並打印方案 { m_count++; print(); } } public: QueenSolution() { init(); } void run() { run(1); // 從第一行開始,註意邊界占用的行數(本例四周都占用了1行或列記錄邊界,所以從1開始) cout << "Total: " << m_count << endl; // 輸出方案個數 } }; int main() { QueenSolution<8> qs; qs.run(); return 0; }
八皇後問題(N皇後問題)
