題目描述

n 皇后問題研究的是如何將 n 個皇后放置在 n×n 的棋盤上，並且使皇后彼此之間不能相互攻擊。

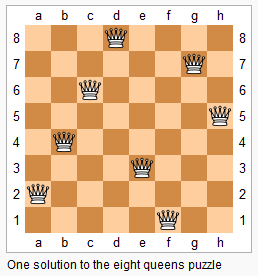
給定一個整數 n，返回 n 皇后不同的解決方案的數量。

解題思路

嗯，這題就是上一題（51.N皇后）的翻版，上一題要求輸出所有解法，這一題卻只要求數量就行了。
所以。。。當然是選擇在51題的基礎上套一層皮啦（滑稽）
51題解法參照：
51.N皇后（N-Queens）

實現程式碼

class Solution {
    public int totalNQueens(int n) {
        boolean[] l = new boolean[n]
 
;
        boolean[] x1 = new boolean[2*n-1];
        boolean[] x2 = new boolean[2*n-1];
        
        List<List<String>> list = new ArrayList();
        List<String> tmp = new ArrayList();
        
        if(n==0)    return 0;
        
        find(list, tmp, n, l, x1, x2);
        
        return
 
 list.size();
    }
    
    public static void find(List<List<String>> list, List<String> tmpList, int n, boolean[] l, boolean[] x1, boolean[] x2){
        if(tmpList.size()==n){
            list.add(new ArrayList<>(tmpList));
            return;
        }
        int i = tmpList.
 
size();
        for(int j=0;j<n;j++){
            if(l[j]==false && x1[j+i]==false && x2[n-1+i-j]==false){
                tmpList.add(append(j, n));
                l[j]=true;
                x1[j+i]=true;
                x2[n-1+i-j]=true;
                find(list, tmpList, n, l, x1, x2);
                l[j]=false;
                x1[j+i]=false;
                x2[n-1+i-j]=false;
                tmpList.remove(tmpList.size()-1);
            }
        }

    }
    
    public static void println(List<String> list){
        for(int i=0;i<list.size();i++)
            System.out.print(list.get(i)+" ");
        System.out.println();
        return;
    }
    
    public static String append(int ind, int n){
        StringBuilder res = new StringBuilder("");
        for(int i=0;i<ind;i++){
            res.append(".");
        }
        res.append("Q");
        for(int i=ind+1;i<n;i++){
            res.append(".");
        }
        return res.toString();
    }
}