普裏姆Prim算法介紹
阿新 • • 發佈:2018-02-24
例如 連通圖 void ron main 二維數組 oid img 介紹
此時,U={A}。
第2步:將頂點B加入到U中。
上一步操作之後,U={A}, V-U={B,C,D,E,F,G};因此,邊(A,B)的權值最小。將頂點B添加到U中;此時,U={A,B}。
第3步:將頂點F加入到U中。
上一步操作之後,U={A,B}, V-U={C,D,E,F,G};因此,邊(B,F)的權值最小。將頂點F添加到U中;此時,U={A,B,F}。
第4步:將頂點E加入到U中。
上一步操作之後,U={A,B,F}, V-U={C,D,E,G};因此,邊(F,E)的權值最小。將頂點E添加到U中;此時,U={A,B,F,E}。
第5步
上一步操作之後,U={A,B,F,E}, V-U={C,D,G};因此,邊(E,D)的權值最小。將頂點D添加到U中;此時,U={A,B,F,E,D}。
第6步:將頂點C加入到U中。
上一步操作之後,U={A,B,F,E,D}, V-U={C,G};因此,邊(D,C)的權值最小。將頂點C添加到U中;此時,U={A,B,F,E,D,C}。
第7步:將頂點G加入到U中。
上一步操作之後,U={A,B,F,E,D,C}, V-U={G};因此,邊(E,G)的權值最小。將頂點G添加到U中;此時,U=V。 



普裏姆(Prim)算法,和克魯斯卡爾算法一樣,是用來求加權連通圖的最小生成樹的算法。
基本思想
對於圖G而言,V是所有頂點的集合;現在,設置兩個新的集合U和T,其中U用於存放G的最小生成樹中的頂點,T存放G的最小生成樹中的邊。
從所有u?U,v?(V-U) (V-U表示出去U的所有頂點)的邊中選取權值最小的邊(u, v),將頂點v加入集合U中,將邊(u,
v)加入集合T中,如此不斷重復,直到U=V為止,最小生成樹構造完畢,這時集合T中包含了最小生成樹中的所有邊。
普裏姆算法圖解
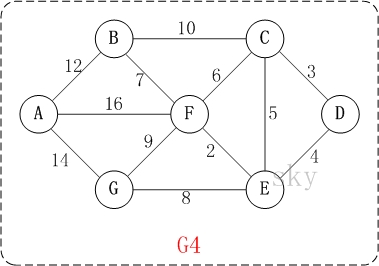
以上圖G4為例,來對普裏姆進行演示(從第一個頂點A開始通過普裏姆算法生成最小生成樹)。

初始狀態:V是所有頂點的集合,即V={A,B,C,D,E,F,G};U和T都是空!
第1步
此時,U={A}。
第2步:將頂點B加入到U中。
上一步操作之後,U={A}, V-U={B,C,D,E,F,G};因此,邊(A,B)的權值最小。將頂點B添加到U中;此時,U={A,B}。
第3步:將頂點F加入到U中。
上一步操作之後,U={A,B}, V-U={C,D,E,F,G};因此,邊(B,F)的權值最小。將頂點F添加到U中;此時,U={A,B,F}。
第4步:將頂點E加入到U中。
上一步操作之後,U={A,B,F}, V-U={C,D,E,G};因此,邊(F,E)的權值最小。將頂點E添加到U中;此時,U={A,B,F,E}。
第5步
上一步操作之後,U={A,B,F,E}, V-U={C,D,G};因此,邊(E,D)的權值最小。將頂點D添加到U中;此時,U={A,B,F,E,D}。
第6步:將頂點C加入到U中。
上一步操作之後,U={A,B,F,E,D}, V-U={C,G};因此,邊(D,C)的權值最小。將頂點C添加到U中;此時,U={A,B,F,E,D,C}。
第7步:將頂點G加入到U中。
上一步操作之後,U={A,B,F,E,D,C}, V-U={G};因此,邊(E,G)的權值最小。將頂點G添加到U中;此時,U=V。
此時,最小生成樹構造完成!它包括的頂點依次是:A B F E D C G
普裏姆算法的代碼說明
以"鄰接矩陣"為例對普裏姆算法進行說明,對於"鄰接表"實現的圖在後面會給出相應的源碼。
1. 基本定義

// 鄰接矩陣
typedef struct _graph
{
char vexs[MAX]; // 頂點集合
int vexnum; // 頂點數
int edgnum; // 邊數
int matrix[MAX][MAX]; // 鄰接矩陣
}Graph, *PGraph;
// 邊的結構體
typedef struct _EdgeData
{
char start; // 邊的起點
char end; // 邊的終點
int weight; // 邊的權重
}EData;

Graph是鄰接矩陣對應的結構體。
vexs用於保存頂點,vexnum是頂點數,edgnum是邊數;matrix則是用於保存矩陣信息的二維數組。例如,matrix[i][j]=1,則表示"頂點i(即vexs[i])"和"頂點j(即vexs[j])"是鄰接點;matrix[i][j]=0,則表示它們不是鄰接點。
EData是鄰接矩陣邊對應的結構體。
2. 普裏姆算法

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF (~(0x1<<31))
typedef struct Graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
} Graph,*PGraph;
typedef struct EdgeData
{
char start;
char end;
int weight;
} EData;
static int get_position(Graph g,char ch)
{
int i;
for(i=0; i<g.vexnum; i++)
if(g.vexs[i]==ch)
return i;
return -1;
}
Graph* create_graph()
{
char vexs[]= {‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘};
int matrix[][7]=
{
{0,12,INF,INF,INF,16,14},
{12,0,10,INF,INF,7,INF},
{INF,10,0,3,5,6,INF},
{INF,INF,3,0,4,INF,INF},
{INF,INF,5,4,0,INF,8},
{16,7,6,INF,2,0,9},
{14,INF,INF,INF,8,9,0}
};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int i,j;
Graph *pG;
if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
return NULL;
memset(pG,0,sizeof(pG));
pG->vexnum=vlen;
for(i=0; i<pG->vexnum; i++)
pG->vexs[i]=vexs[i];
for(i=0; i<pG->vexnum; i++)
for(j=0; j<pG->vexnum; j++)
pG->matrix[i][j]=matrix[i][j];
for(i=0; i<pG->vexnum; i++)
{
for(j=0; j<pG->vexnum; j++)
{
if(i!=j&&pG->matrix[i][j]!=INF)
pG->edgnum++;
}
}
pG->edgnum/=2;
return pG;
}
void print_graph(Graph G)
{
int i,j;
printf("Matrix Graph: \n");
for(i=0; i<G.vexnum; i++)
{
for(j=0; j<G.vexnum; j++)
printf("%10d ",G.matrix[i][j]);
printf("\n");
}
}
EData* get_edges(Graph G)
{
EData *edges;
edges=(EData*)malloc(G.edgnum*sizeof(EData));
int i,j;
int index=0;
for(i=0; i<G.vexnum; i++)
{
for(j=i+1; j<G.vexnum; j++)
{
if(G.matrix[i][j]!=INF)
{
edges[index].start=G.vexs[i];
edges[index].end=G.vexs[j];
edges[index].weight=G.matrix[i][j];
index++;
}
}
}
return edges;
}
void prim(Graph G,int start)
{
int min,i,j,k,m,n,sum;
int index=0;
char prim[MAX];
int weight[MAX];
prim[index++]=G.vexs[start];
for(i=0; i<G.vexnum; i++)
weight[i]=G.matrix[start][i];
weight[start]=0;
for(i=0; i<G.vexnum; i++)
{
//i用來控制循環的次數,每次加入一個結點,但是因為start已經加入,所以當i為start是跳過
if(start==i)
continue;
j=0;
k=0;
min=INF;
for(k=0; k<G.vexnum; k++)
{
if(weight[k]&&weight[k]<min)
{
min=weight[k];
j=k;
}
}
sum+=min;
prim[index++]=G.vexs[j];
weight[j]=0;
for(k=0; k<G.vexnum; k++)
{
if(weight[k]&&G.matrix[j][k]<weight[k])
weight[k]=G.matrix[j][k];
}
}
// 計算最小生成樹的權值
sum = 0;
for (i = 1; i < index; i++)
{
min = INF;
// 獲取prims[i]在G中的位置
n = get_position(G, prim[i]);
// 在vexs[0...i]中,找出到j的權值最小的頂點。
for (j = 0; j < i; j++)
{
m = get_position(G, prim[j]);
if (G.matrix[m][n]<min)
min = G.matrix[m][n];
}
sum += min;
}
printf("PRIM(%c)=%d: ", G.vexs[start], sum);
for (i = 0; i < index; i++)
printf("%c ", prim[i]);
printf("\n");
}
int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
prim(*pG,0);
}

運行結果:

普裏姆Prim算法介紹
