數據算法與結構
http://dongxicheng.org/structure/structure-algorithm-summary/
https://www.cnblogs.com/zhuzhenwei918/p/6227448.html 略
http://blog.csdn.net/l_215851356/article/details/77659462
http://blog.fishc.com/category/structure/page/10 小甲魚
http://www.cnblogs.com/alex3714/articles/5474411.html
.算法定義
算法(Algorithm)是指解題方案的準確而完整的描述,是一系列解決問題的清晰指令,算法代表著用系統的方法描述解決問題的策略機制。也就是說,能夠對一定規範的輸入,在有限時間內獲得所要求的輸出。如果一個算法有缺陷,或不適合於某個問題,執行這個算法將不會解決這個問題。不同的算法可能用不同的時間、空間或效率來完成同樣的任務。一個算法的優劣可以用空間復雜度與時間復雜度來衡量。
一個算法應該具有以下七個重要的特征:
①有窮性(Finiteness):算法的有窮性是指算法必須能在執行有限個步驟之後終止;
②確切性(Definiteness):算法的每一步驟必須有確切的定義;
③輸入項(Input):一個算法有0個或多個輸入,以刻畫運算對象的初始情況,所謂0個輸 入是指算法本身定出了初始條件;
④輸出項(Output):一個算法有一個或多個輸出,以反映對輸入數據加工後的結果。沒 有輸出的算法是毫無意義的;
⑤可行性(Effectiveness):算法中執行的任何計算步驟都是可以被分解為基本的可執行 的操作步,即每個計算步都可以在有限時間內完成(也稱之為有效性);
⑥高效性(High efficiency):執行速度快,占用資源少;
⑦健壯性(Robustness):對數據響應正確。
2. 時間復雜度
計算機科學中,算法的時間復雜度是一個函數,它定量描述了該算法的運行時間,時間復雜度常用大O符號(大O符號(Big O notation)是用於描述函數漸進行為的數學符號。更確切地說,它是用另一個(通常更簡單的)函數來描述一個函數數量級的漸近上界。在數學中,它一般用來刻畫被截斷的無窮級數尤其是漸近級數的剩余項;在計算機科學中,它在分析算法復雜性的方面非常有用。)表述,使用這種方式時,時間復雜度可被稱為是漸近的,它考察當輸入值大小趨近無窮時的情況。
大O,簡而言之可以認為它的含義是“order of”(大約是)。
無窮大漸近
大O符號在分析算法效率的時候非常有用。舉個例子,解決一個規模為 n 的問題所花費的時間(或者所需步驟的數目)可以被求得:T(n) = 4n^2 - 2n + 2。
當 n 增大時,n^2; 項將開始占主導地位,而其他各項可以被忽略——舉例說明:當 n = 500,4n^2; 項是 2n 項的1000倍大,因此在大多數場合下,省略後者對表達式的值的影響將是可以忽略不計的。
數學表示掃盲貼 http://www.cnblogs.com/alex3714/articles/5910253.html
|
定義:如果一個問題的規模是n,解這一問題的某一算法所需要的時間為T(n),它是n的某一函數 T(n)稱為這一算法的“時間復雜性”。 當輸入量n逐漸加大時,時間復雜性的極限情形稱為算法的“漸近時間復雜性”。 我們常用大O表示法表示時間復雜性,註意它是某一個算法的時間復雜性。大O表示只是說有上界,由定義如果f(n)=O(n),那顯然成立f(n)=O(n^2),它給你一個上界,但並不是上確界,但人們在表示的時候一般都習慣表示前者。 此外,一個問題本身也有它的復雜性,如果某個算法的復雜性到達了這個問題復雜性的下界,那就稱這樣的算法是最佳算法。 “大O記法”:在這種描述中使用的基本參數是 n,即問題實例的規模,把復雜性或運行時間表達為n的函數。這裏的“O”表示量級 (order),比如說“二分檢索是 O(logn)的”,也就是說它需要“通過logn量級的步驟去檢索一個規模為n的數組”記法 O ( f(n) )表示當 n增大時,運行時間至多將以正比於 f(n)的速度增長。 這種漸進估計對算法的理論分析和大致比較是非常有價值的,但在實踐中細節也可能造成差異。例如,一個低附加代價的O(n2)算法在n較小的情況下可能比一個高附加代價的 O(nlogn)算法運行得更快。當然,隨著n足夠大以後,具有較慢上升函數的算法必然工作得更快。 O(1) Temp=i;i=j;j=temp; 以上三條單個語句的頻度均為1,該程序段的執行時間是一個與問題規模n無關的常數。算法的時間復雜度為常數階,記作T(n)=O(1)。如果算法的執行時間不隨著問題規模n的增加而增長,即使算法中有上千條語句,其執行時間也不過是一個較大的常數。此類算法的時間復雜度是O(1)。 O(n^2) 2.1. 交換i和j的內容 sum=0; (一次) for(i=1;i<=n;i++) (n次 ) for(j=1;j<=n;j++) (n^2次 ) sum++; (n^2次 ) 解:T(n)=2n^2+n+1 =O(n^2) 2.2. for (i=1;i<n;i++) { y=y+1; ① for (j=0;j<=(2*n);j++) x++; ② } 解: 語句1的頻度是n-1 語句2的頻度是(n-1)*(2n+1)=2n^2-n-1 f(n)=2n^2-n-1+(n-1)=2n^2-2 該程序的時間復雜度T(n)=O(n^2). O(n) 2.3. a=0; b=1; ① for (i=1;i<=n;i++) ② { s=a+b; ③ b=a; ④ a=s; ⑤ } 解:語句1的頻度:2, 語句2的頻度: n, 語句3的頻度: n-1, 語句4的頻度:n-1, 語句5的頻度:n-1, T(n)=2+n+3(n-1)=4n-1=O(n). O(log2n ) 2.4. i=1; ① while (i<=n) i=i*2; ② 解: 語句1的頻度是1, 設語句2的頻度是f(n), 則:2^f(n)<=n;f(n)<=log2n 取最大值f(n)= log2n, T(n)=O(log2n ) O(n^3) 2.5. for(i=0;i<n;i++) { for(j=0;j<i;j++) { for(k=0;k<j;k++) x=x+2; } } 解:當i=m, j=k的時候,內層循環的次數為k當i=m時, j 可以取 0,1,...,m-1 , 所以這裏最內循環共進行了0+1+...+m-1=(m-1)m/2次所以,i從0取到n, 則循環共進行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以時間復雜度為O(n^3). 我們還應該區分算法的最壞情況的行為和期望行為。如快速排序的最 壞情況運行時間是 O(n^2),但期望時間是 O(nlogn)。通過每次都仔細 地選擇基準值,我們有可能把平方情況 (即O(n^2)情況)的概率減小到幾乎等於 0。在實際中,精心實現的快速排序一般都能以 (O(nlogn)時間運行。 下面是一些常用的記法: 訪問數組中的元素是常數時間操作,或說O(1)操作。一個算法如 果能在每個步驟去掉一半數據元素,如二分檢索,通常它就取 O(logn)時間。用strcmp比較兩個具有n個字符的串需要O(n)時間。常規的矩陣乘算法是O(n^3),因為算出每個元素都需要將n對 元素相乘並加到一起,所有元素的個數是n^2。 指數時間算法通常來源於需要求出所有可能結果。例如,n個元 素的集合共有2n個子集,所以要求出所有子集的算法將是O(2n)的。指數算法一般說來是太復雜了,除非n的值非常小,因為,在 這個問題中增加一個元素就導致運行時間加倍。不幸的是,確實有許多問題 (如著名的“巡回售貨員問題” ),到目前為止找到的算法都是指數的。如果我們真的遇到這種情況,通常應該用尋找近似最佳結果的算法替代之。 |
常用排序
|
名稱 |
復雜度 |
說明 |
備註 |
|
冒泡排序 |
O(N*N) |
將待排序的元素看作是豎著排列的“氣泡”,較小的元素比較輕,從而要往上浮 |
|
|
插入排序 Insertion sort |
O(N*N) |
逐一取出元素,在已經排序的元素序列中從後向前掃描,放到適當的位置 |
起初,已經排序的元素序列為空 |
|
選擇排序 |
O(N*N) |
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然後,再從剩余未排序元素中繼續尋找最小元素,然後放到排序序列末尾。以此遞歸。 |
|
|
快速排序 Quick Sort |
O(n *log2(n)) |
先選擇中間值,然後把比它小的放在左邊,大的放在右邊(具體的實現是從兩邊找,找到一對後交換)。然後對兩邊分別使用這個過程(遞歸)。 |
|
|
堆排序HeapSort |
O(n *log2(n)) |
利用堆(heaps)這種數據結構來構造的一種排序算法。堆是一個近似完全二叉樹結構,並同時滿足堆屬性:即子節點的鍵值或索引總是小於(或者大於)它的父節點。 |
近似完全二叉樹 |
|
希爾排序 SHELL |
O(n1+£) 0<£<1 |
選擇一個步長(Step) ,然後按間隔為步長的單元進行排序.遞歸,步長逐漸變小,直至為1. |
|
|
箱排序 |
O(n) |
設置若幹個箱子,把關鍵字等於 k 的記錄全都裝入到第k 個箱子裏 ( 分配 ) ,然後按序號依次將各非空的箱子首尾連接起來 ( 收集 ) 。 |
分配排序的一種:通過" 分配 " 和 " 收集 " 過程來實現排序。 |
冒泡排序(Bubble Sort)
冒泡排序(Bubble Sort),是一種計算機科學領域的較簡單的排序算法。 它重復地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重復地進行直到沒有再需要交換,也就是說該數列已經排序完成。 這個算法的名字由來是因為越大的元素會經由交換慢慢“浮”到數列的頂端,故名。| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
data_set = [ 9,1,22,31,45,3,6,2,11 ]
loop_count = 0
for j in range(len(data_set)):
for i in range(len(data_set) - j- 1): # -1 是因為每次比對的都 是i 與i +1,不減1的話,最後一次對比會超出list 獲取範圍,-j是因為,每一次大loop就代表排序好了一個最大值,放在了列表最後面,下次loop就不用再運算已經排序好了的值 了
if data_set[i] > data_set[i+1]: #switch
tmp = data_set[i]
data_set[i] = data_set[i+1]
data_set[i+1] = tmp
loop_count +=1
print(data_set)
print(data_set)
print("loop times", loop_count)
|
選擇排序
The algorithm works by selecting the smallest unsorted item and then swapping it with the item in the next position to be filled.
The selection sort works as follows: you look through the entire array for the smallest element, once you find it you swap it (the smallest element) with the first element of the array. Then you look for the smallest element in the remaining array (an array without the first element) and swap it with the second element. Then you look for the smallest element in the remaining array (an array without first and second elements) and swap it with the third element, and so on. Here is an example,
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
data_set = [ 9,1,22,31,45,3,6,2,11 ]
smallest_num_index = 0 #初始列表最小值,默認為第一個
loop_count = 0
for j in range(len(data_set)):
for i in range(j,len(data_set)):
if data_set[i] < data_set[smallest_num_index]: #當前值 比之前選出來的最小值 還要小,那就把它換成最小值
smallest_num_index = i
loop_count +=1
else:
print("smallest num is ",data_set[smallest_num_index])
tmp = data_set[smallest_num_index]
data_set[smallest_num_index] = data_set[j]
data_set[j] = tmp
print(data_set)
print("loop times", loop_count)
|
The worst-case runtime complexity is O(n2).
插入排序(Insertion Sort)
插入排序(Insertion Sort)的基本思想是:將列表分為2部分,左邊為排序好的部分,右邊為未排序的部分,循環整個列表,每次將一個待排序的記錄,按其關鍵字大小插入到前面已經排好序的子序列中的適當位置,直到全部記錄插入完成為止。

插入排序非常類似於整撲克牌。
在開始摸牌時,左手是空的,牌面朝下放在桌上。接著,一次從桌上摸起一張牌,並將它插入到左手一把牌中的正確位置上。為了找到這張牌的正確位置,要將它與手中已有的牌從右到左地進行比較。無論什麽時候,左手中的牌都是排好序的。
也許你沒有意識到,但其實你的思考過程是這樣的:現在抓到一張7,把它和手裏的牌從右到左依次比較,7比10小,應該再往左插,7比5大,好,就插這裏。為什麽比較了10和5就可以確定7的位置?為什麽不用再比較左邊的4和2呢?因為這裏有一個重要的前提:手裏的牌已經是排好序的。現在我插了7之後,手裏的牌仍然是排好序的,下次再抓到的牌還可以用這個方法插入。編程對一個數組進行插入排序也是同樣道理,但和插入撲克牌有一點不同,不可能在兩個相鄰的存儲單元之間再插入一個單元,因此要將插入點之後的數據依次往後移動一個單元。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
source = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
for index in range(1,len(source)):
current_val = source[index] #先記下來每次大循環走到的第幾個元素的值
position = index
while position > 0 and source[position-1] > current_val: #當前元素的左邊的緊靠的元素比它大,要把左邊的元素一個一個的往右移一位,給當前這個值插入到左邊挪一個位置出來
source[position] = source[position-1] #把左邊的一個元素往右移一位
position -= 1 #只一次左移只能把當前元素一個位置 ,還得繼續左移只到此元素放到排序好的列表的適當位置 為止
source[position] = current_val #已經找到了左邊排序好的列表裏不小於current_val的元素的位置,把current_val放在這裏
print(source)
|
結果:
[77, 92, 67, 8, 6, 84, 55, 85, 43, 67]
[67, 77, 92, 8, 6, 84, 55, 85, 43, 67]
[8, 67, 77, 92, 6, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 92, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 84, 92, 55, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 92, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 85, 92, 43, 67]
[6, 8, 43, 55, 67, 77, 84, 85, 92, 67]
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]
#更容易理解的版本
 插入排序
插入排序
快速排序(quick sort)
設要排序的數組是A[0]……A[N-1],首先任意選取一個數據(通常選用數組的第一個數)作為關鍵數據,然後將所有比它小的數都放到它前面,所有比它大的數都放到它後面,這個過程稱為一趟快速排序。值得註意的是,快速排序不是一種穩定的排序算法,也就是說,多個相同的值的相對位置也許會在算法結束時產生變動
註:在待排序的文件中,若存在多個關鍵字相同的記錄,經過排序後這些具有相同關鍵字的記錄之間的相對次序保持不變,該排序方法是穩定的;若具有相同關鍵字的記錄之間的相對次序發生改變,則稱這種排序方法是不穩定的。
要註意的是,排序算法的穩定性是針對所有輸入實例而言的。即在所有可能的輸入實例中,只要有一個實例使得算法不滿足穩定性要求,則該排序算法就是不穩定的。
排序演示
示例
假設用戶輸入了如下數組:| 下標 | 0 | 1 | 2 | 3 | 4 | 5 |
| 數據 | 6 | 2 | 7 | 3 | 8 | 9 |
| 下標 | 0 | 1 | 2 | 3 | 4 | 5 |
| 數據 | 3 | 2 | 7 | 6 | 8 | 9 |
| 下標 | 0 | 1 | 2 | 3 | 4 | 5 |
| 數據 | 3 | 2 | 6 | 7 | 8 | 9 |
| 下標 | 0 | 1 | 2 | 3 | 4 | 5 |
| 數據 | 3 | 2 | 6 | 7 | 8 | 9 |
二叉樹
樹的特征和定義
樹是一種重要的非線性數據結構,直觀地看,它是數據元素(在樹中稱為結點)按分支關系組織起來的結構,很象自然界中的樹那樣。樹結構在客觀世界中廣泛存在,如人類社會的族譜和各種社會組織機構都可用樹形象表示。樹在計算機領域中也得到廣泛應用,如在編譯源程序時,可用樹表示源程序的語法結構。又如在數據庫系統中,樹型結構也是信息的重要組織形式之一。一切具有層次關系的問題都可用樹來描述。
樹(Tree)是元素的集合。我們先以比較直觀的方式介紹樹。下面的數據結構是一個樹:

樹有多個節點(node),用以儲存元素。某些節點之間存在一定的關系,用連線表示,連線稱為邊(edge)。邊的上端節點稱為父節點,下端稱為子節點。樹像是一個不斷分叉的樹根。
每個節點可以有多個子節點(children),而該節點是相應子節點的父節點(parent)。比如說,3,5是6的子節點,6是3,5的父節點;1,8,7是3的子節點, 3是1,8,7的父節點。樹有一個沒有父節點的節點,稱為根節點(root),如圖中的6。沒有子節點的節點稱為葉節點(leaf),比如圖中的1,8,9,5節點。從圖中還可以看到,上面的樹總共有4個層次,6位於第一層,9位於第四層。樹中節點的最大層次被稱為深度。也就是說,該樹的深度(depth)為4。
如果我們從節點3開始向下看,而忽略其它部分。那麽我們看到的是一個以節點3為根節點的樹:

三角形代表一棵樹
再進一步,如果我們定義孤立的一個節點也是一棵樹的話,原來的樹就可以表示為根節點和子樹(subtree)的關系:

上述觀察實際上給了我們一種嚴格的定義樹的方法:
1. 樹是元素的集合。
2. 該集合可以為空。這時樹中沒有元素,我們稱樹為空樹 (empty tree)。
3. 如果該集合不為空,那麽該集合有一個根節點,以及0個或者多個子樹。根節點與它的子樹的根節點用一個邊(edge)相連。
上面的第三點是以遞歸的方式來定義樹,也就是在定義樹的過程中使用了樹自身(子樹)。由於樹的遞歸特征,許多樹相關的操作也可以方便的使用遞歸實現。我們將在後面看到。
樹的實現
樹的示意圖已經給出了樹的一種內存實現方式: 每個節點儲存元素和多個指向子節點的指針。然而,子節點數目是不確定的。一個父節點可能有大量的子節點,而另一個父節點可能只有一個子節點,而樹的增刪節點操作會讓子節點的數目發生進一步的變化。這種不確定性就可能帶來大量的內存相關操作,並且容易造成內存的浪費。
一種經典的實現方式如下:

樹的內存實現
擁有同一父節點的兩個節點互為兄弟節點(sibling)。上圖的實現方式中,每個節點包含有一個指針指向第一個子節點,並有另一個指針指向它的下一個兄弟節點。這樣,我們就可以用統一的、確定的結構來表示每個節點。
計算機的文件系統是樹的結構,比如Linux文件管理背景知識中所介紹的。在UNIX的文件系統中,每個文件(文件夾同樣是一種文件),都可以看做是一個節點。非文件夾的文件被儲存在葉節點。文件夾中有指向父節點和子節點的指針(在UNIX中,文件夾還包含一個指向自身的指針,這與我們上面見到的樹有所區別)。在git中,也有類似的樹狀結構,用以表達整個文件系統的版本變化 (參考版本管理三國誌)。

二叉樹:
二叉樹是由n(n≥0)個結點組成的有限集合、每個結點最多有兩個子樹的有序樹。它或者是空集,或者是由一個根和稱為左、右子樹的兩個不相交的二叉樹組成。
特點:
(1)二叉樹是有序樹,即使只有一個子樹,也必須區分左、右子樹;
(2)二叉樹的每個結點的度不能大於2,只能取0、1、2三者之一;
(3)二叉樹中所有結點的形態有5種:空結點、無左右子樹的結點、只有左子樹的結點、只有右子樹的結點和具有左右子樹的結點。

二叉樹(binary)是一種特殊的樹。二叉樹的每個節點最多只能有2個子節點:

二叉樹
由於二叉樹的子節點數目確定,所以可以直接采用上圖方式在內存中實現。每個節點有一個左子節點(left children)和右子節點(right children)。左子節點是左子樹的根節點,右子節點是右子樹的根節點。
如果我們給二叉樹加一個額外的條件,就可以得到一種被稱作二叉搜索樹(binary search tree)的特殊二叉樹。二叉搜索樹要求:每個節點都不比它左子樹的任意元素小,而且不比它的右子樹的任意元素大。
(如果我們假設樹中沒有重復的元素,那麽上述要求可以寫成:每個節點比它左子樹的任意節點大,而且比它右子樹的任意節點小)

二叉搜索樹,註意樹中元素的大小
二叉搜索樹可以方便的實現搜索算法。在搜索元素x的時候,我們可以將x和根節點比較:
1. 如果x等於根節點,那麽找到x,停止搜索 (終止條件)
2. 如果x小於根節點,那麽搜索左子樹
3. 如果x大於根節點,那麽搜索右子樹
二叉搜索樹所需要進行的操作次數最多與樹的深度相等。n個節點的二叉搜索樹的深度最多為n,最少為log(n)。
二叉樹的遍歷
遍歷即將樹的所有結點訪問且僅訪問一次。按照根節點位置的不同分為前序遍歷,中序遍歷,後序遍歷。
前序遍歷:根節點->左子樹->右子樹
中序遍歷:左子樹->根節點->右子樹
後序遍歷:左子樹->右子樹->根節點
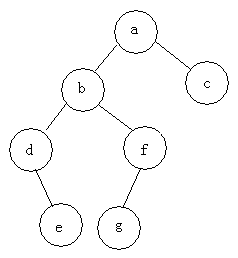
例如:求下面樹的三種遍歷
前序遍歷:abdefgc
中序遍歷:debgfac
後序遍歷:edgfbca
二叉樹的類型
(1)完全二叉樹——若設二叉樹的高度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第h層有葉子結點,並且葉子結點都是從左到右依次排布,這就是完全二叉樹。 (2)滿二叉樹——除了葉結點外每一個結點都有左右子葉且葉子結點都處在最底層的二叉樹。 (3)平衡二叉樹——平衡二叉樹又被稱為AVL樹(區別於AVL算法),它是一棵二叉排序樹,且具有以下性質:它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,並且左右兩個子樹都是一棵平衡二叉樹如何判斷一棵樹是完全二叉樹?按照定義,
教材上的說法:一個深度為k,節點個數為 2^k - 1 的二叉樹為滿二叉樹。這個概念很好理解,
就是一棵樹,深度為k,並且沒有空位。
首先對滿二叉樹按照廣度優先遍歷(從左到右)的順序進行編號。
一顆深度為k二叉樹,有n個節點,然後,也對這棵樹進行編號,如果所有的編號都和滿二叉樹對應,那麽這棵樹是完全二叉樹。

如何判斷平衡二叉樹?

(b)左邊的圖 左子數的高度為3,右子樹的高度為1,相差超過1
(b)右邊的圖 -2的左子樹高度為0 右子樹的高度為2,相差超過1
二叉樹遍歷實現
+ View Code
堆排序
堆排序,顧名思義,就是基於堆。因此先來介紹一下堆的概念。
堆分為最大堆和最小堆,其實就是完全二叉樹。最大堆要求節點的元素都要大於其孩子,最小堆要求節點元素都小於其左右孩子,兩者對左右孩子的大小關系不做任何要求,其實很好理解。有了上面的定義,我們可以得知,處於最大堆的根節點的元素一定是這個堆中的最大值。其實我們的堆排序算法就是抓住了堆的這一特點,每次都取堆頂的元素,將其放在序列最後面,然後將剩余的元素重新調整為最大堆,依次類推,最終得到排序的序列。
堆排序就是把堆頂的最大數取出,
將剩余的堆繼續調整為最大堆,具體過程在第二塊有介紹,以遞歸實現
剩余部分調整為最大堆後,再次將堆頂的最大數取出,再將剩余部分調整為最大堆,這個過程持續到剩余數只有一個時結束

+ View Code
 人類能理解的版本
人類能理解的版本
希爾排序(shell sort)
希爾排序(Shell Sort)是插入排序的一種。也稱縮小增量排序,是直接插入排序算法的一種更高效的改進版本,該方法的基本思想是:先將整個待排元素序列分割成若幹個子序列(由相隔某個“增量”的元素組成的)分別進行直接插入排序,然後依次縮減增量再進行排序,待整個序列中的元素基本有序(增量足夠小)時,再對全體元素進行一次直接插入排序。因為直接插入排序在元素基本有序的情況下(接近最好情況),效率是很高的,因此希爾排序在時間效率比直接插入排序有較大提高

首先要明確一下增量的取法:
第一次增量的取法為: d=count/2;
第二次增量的取法為: d=(count/2)/2;
最後一直到: d=1;
看上圖觀測的現象為:
d=3時:將40跟50比,因50大,不交換。
將20跟30比,因30大,不交換。
將80跟60比,因60小,交換。
d=2時:將40跟60比,不交換,拿60跟30比交換,此時交換後的30又比前面的40小,又要將40和30交換,如上圖。
將20跟50比,不交換,繼續將50跟80比,不交換。
d=1時:這時就是前面講的插入排序了,不過此時的序列已經差不多有序了,所以給插入排序帶來了很大的性能提高。
數據算法與結構