題目鏈接：http://codeforces.com/problemset/problem/466/C

題目：

You‘ve got array a[1], a[2], ..., a[n], consisting of n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.

More formally, you need to find the number of such pairs of indices i

(2 ≤ i ≤ j ≤ n - 1), that .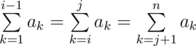

The first line contains integer n (1 ≤ n ≤ 5·105), showing how many numbers are in the array. The second line contains n integers a[1], a[2], ..., a

Print a single integer — the number of ways to split the array into three parts with the same sum.

5
1 2 3 0 3

2

4
0 1 -1 0

1

2
 
4 1

0

題解：前綴和暴力，找下規律。（好像還能用DP解，明天起來再看看！）

 1 #include <map>
 2 #include <cstdio>
 3 #include <iostream>
 4 #include <algorithm>
 5 using namespace std;
 6 
 7 typedef long long LL;
 8 const int N=1e6;
 9 LL f[N],c1[N],c2[N];
10 
11 int main(){
12     LL n,ans=0,cnt=0;
13     scanf("%lld",&n);
14     for(int i=1;i<=n;i++){
15         scanf("%lld",&f[i]);
16         f[i]+=f[i-1];
17         if(!f[i]) cnt++;
18     }
19     if(f[n]%3!=0) {printf("0\n");return 0;}
20     if(f[n]==0){
21         printf("%lld\n",(cnt-1)*(cnt-2)/2);
22         return 0;
23     }
24 
25     for(int i=1;i<=n;i++){
26         c1[i]=c1[i-1];c2[i]=c2[i-1];
27         if(f[i]==(f[n]/3)) c1[i]++;
28         if(f[i]==(f[n]/3*2)) c2[i]++;
29     }
30     for(int i=2;i<n;i++){
31         if(f[i]==(f[n]/3*2)) ans+=c1[i];
32     }
33     printf("%lld\n",ans);
34     return 0;
35 }

CF 466C Number of Ways（數學 / 思維 / DP）