深度優先搜索算法的概念

　　與廣度優先搜索算法不同，深度優先搜索算法類似與樹的先序遍歷。這種搜索算法所遵循的搜索策略是盡可能“深”地搜索一個圖。它的基本思想如下：首先訪問圖中某一個起始頂點v，然後由v出發，訪問與v相鄰且未被訪問的任一頂點w1,再訪問與w1鄰接且未被訪問的任一頂點w2，….重復上述過程。當不能再繼續向下訪問時，依次退回到最近被訪問的頂點，若它還有鄰接頂點未被訪問過，則從該點開始繼續上述搜索過程，直到圖中所有頂點均被訪問過為止(還是舉相同的例子，從你開始遍歷你的所有親戚，例如：先訪問你的兒子，再從你的兒子繼續訪問你的兒子的兒子，直到你的兒子是最後一個頂點，再回退回上一層，訪問你兒子的女兒，再訪問你兒子的女兒的兒子….依此類推，直到你的所有親戚都被訪問過一次為止，這和廣度優先搜索的算法區別還是很大的)

算法偽代碼

　　DFS采用的是遞歸的過程，所以這個過程需要一個遞歸工作的輔助棧，偽代碼如下：
　　

bool visited[MAX_VERTEX_NUM];//訪問標記數組

void DFSTraverse(Graph G){
//對圖G進行深度優先遍歷，訪問函數為visit（）
    for(v=0;v<G.vexnum;++i)
        visited[v]=false;//初始化所有頂點的數據，false表示未曾訪問過
    for(v=0;v<G.vexnum;++v)
        if(!visited[v])
            DFS(G,v);//這裏從0遍歷到最後一個頂點是為了防止有極端情況出現：可能存在頂點wi無法從頂點w0遍歷到，所以需要對它也調用一次DFS算法
}

void DFS(Graph G,int v){
//從頂點v出發，采用遞歸的思想，深度優先遍歷圖G
    visit（v）;//訪問頂點v
    visited[v]=true;//設置這個頂點為已經訪問過

    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
        if(!visited[w])
            DFS(G,w);//遞歸調用查找第一個未被訪問的鄰接頂點
}
 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20

實例及分析

　　
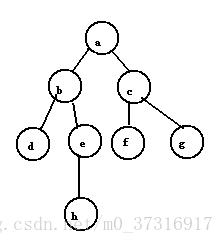
　　首先訪問a，並置a為已經訪問；然後訪問與a鄰接且未被訪問的頂點b，置b為已經訪問，然後訪問與b鄰接且未被訪問的頂點d，置d為已經訪問。此時d已經沒有未被訪問過的鄰接點，這時候返回上一個訪問過的頂點b，訪問與其鄰接且未被訪問的頂點e，置e為已經訪問……。依此類推，直到途中所有的頂點都被訪問一次且僅僅被訪問一次，遍歷結果為abdehcfg。

DFS算法的性能分析

　　DFS算法是一個遞歸算法，需要借助一個遞歸工作棧，所以它的空間復雜度是O(|V|)。
　　遍歷圖的過程實際上是對每個頂點查找其鄰接點的過程，其耗費的時間取決於所采用的存儲結構，當以鄰接矩陣表示時，查找每個頂點的臨界點所需時間為O（|V|），故總的時間復雜度為O(|V|2)

深度優先搜索算法的概念