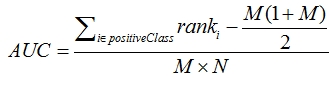ROC 曲線,以及AUC計算方式
ROC曲線:
roc曲線:接收者操作特征(receiveroperating characteristic),roc曲線上每個點反映著對同一信號刺激的感受性。
ROC曲線的橫軸:
負正類率(false postive rate FPR)特異度,劃分實例中所有負例占所有負例的比例;(1-Specificity)
預測為正樣本但是實際為負樣本的數目占所有負樣本的數目的比例
ROC 縱軸:
真正類率(true postive rate TPR)靈敏度,Sensitivity(正類覆蓋率)
預測為正樣本實際也為正樣本的數目 占 所有正樣本數目的比例
AUC計算方式:
一個關於AUC的很有趣的性質是,它和Wilcoxon-Mann-Witney Test是等價的。這個等價關系的證明留在下篇帖子中給出。而Wilcoxon-Mann-Witney Test就是測試任意給一個正類樣本和一個負類樣本,正類樣本的score有多大的概率大於負類樣本的score。有了這個定義,我們就得到了另外一中計 算AUC的辦法:得到這個概率。我們知道,在有限樣本中我們常用的得到概率的辦法就是通過頻率來估計之。這種估計隨著樣本規模的擴大而逐漸逼近真實值。這 和上面的方法中,樣本數越多,計算的AUC越準確類似,也和計算積分的時候,小區間劃分的越細,計算的越準確是同樣的道理。具體來說就是統計一下所有的 M×N(M為正類樣本的數目,N為負類樣本的數目)個正負樣本對中,有多少個組中的正樣本的score大於負樣本的score。當二元組中正負樣本的 score相等的時候,按照0.5計算。然後除以MN。實現這個方法的復雜度為O(n^2)。n為樣本數(即n=M+N)
3. 第三種方法實際上和上述第二種方法是一樣的,但是復雜度減小了。它也是首先對score從大到小排序,然後令最大score對應的sample 的rank為n,第二大score對應sample的rank為n-1,以此類推。然後把所有的正類樣本的rank相加,再減去M-1種兩個正樣本組合的情況。得到的就是所有的樣本中有多少對正類樣本的score大於負類樣本的score。然後再除以M×N。即
公式解釋:
1、為了求的組合中正樣本的score值大於負樣本,如果所有的正樣本score值都是大於負樣本的,那麽第一位與任意的進行組合score值都要大,我們取它的rank值為n,但是n-1中有M-1是正樣例和正樣例的組合這種是不在統計範圍內的(為計算方便我們取n組,相應的不符合的有M個),所以要減掉,那麽同理排在第二位的n-1,會有M-1個是不滿足的,依次類推,故得到後面的公式M*(M+1)/2,我們可以驗證在正樣本score都大於負樣本的假設下,AUC的值為1
2、根據上面的解釋,不難得出,rank的值代表的是能夠產生score前大後小的這樣的組合數,但是這裏包含了(正,正)的情況,所以要減去這樣的組(即排在它後面正例的個數),即可得到上面的公式
另外,特別需要註意的是,再存在score相等的情況時,對相等score的樣本,需要 賦予相同的rank(無論這個相等的score是出現在同類樣本還是不同類的樣本之間,都需要這樣處理)。具體操作就是再把所有這些score相等的樣本 的rank取平均。然後再使用上述公式。
參考資料:
https://blog.csdn.net/pzy20062141/article/details/48711355
ROC 曲線,以及AUC計算方式