題目傳送門

題目描述

小城和小華都是熱愛數學的好學生，最近，他們不約而同地迷上了數獨遊戲，好勝的他

們想用數獨來一比高低。但普通的數獨對他們來說都過於簡單了，於是他們向 Z 博士請教，

Z 博士拿出了他最近發明的“靶形數獨”，作為這兩個孩子比試的題目。

靶形數獨的方格同普通數獨一樣，在 9 格寬×9 格高的大九宮格中有 9 個 3 格寬×3 格

高的小九宮格（用粗黑色線隔開的）。在這個大九宮格中，有一些數字是已知的，根據這些數字，利用邏輯推理，在其他的空格上填入 1 到 9 的數字。每個數字在每個小九宮格內不能

重復出現，每個數字在每行、每列也不能重復出現。但靶形數獨有一點和普通數獨不同，即

每一個方格都有一個分值，而且如同一個靶子一樣，離中心越近則分值越高。（如圖）

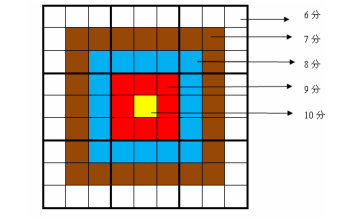
上圖具體的分值分布是：最裏面一格（黃色區域）為 10 分，黃色區域外面的一圈（紅

色區域）每個格子為 9 分，再外面一圈（藍色區域）每個格子為 8 分，藍色區域外面一圈（棕

色區域）每個格子為 7 分，最外面一圈（白色區域）每個格子為 6 分，如上圖所示。比賽的

要求是：每個人必須完成一個給定的數獨（每個給定數獨可能有不同的填法），而且要爭取

更高的總分數。而這個總分數即每個方格上的分值和完成這個數獨時填在相應格上的數字

的乘積的總和

總分數即每個方格上的分值和完成這個數獨時填在相應格上的數字

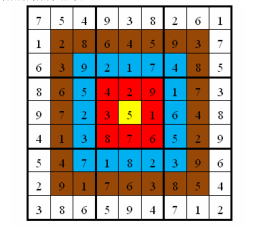
的乘積的總和。如圖，在以下的這個已經填完數字的靶形數獨遊戲中，總分數為 2829。遊戲規定，將以總分數的高低決出勝負。

由於求勝心切，小城找到了善於編程的你，讓你幫他求出，對於給定的靶形數獨，能

夠得到的最高分數。

輸入輸出格式

輸入格式：

一共 9 行。每行 9 個整數（每個數都在 0―9 的範圍內），表示一個尚未填滿的數獨方

格，未填的空格用“0”表示。每兩個數字之間用一個空格隔開。

輸出格式：

輸出共 1 行。

輸出可以得到的靶形數獨的最高分數。如果這個數獨無解，則輸出整數-1。

輸入輸出樣例

7 0 0 9 0 0 0 0 1 
1 0 0 0 0 5 9 0 0 
0 0 0 2 0 0 0 8 0 
0 0 5 0 2 0 0 0 3 
0 0 0 0 0 0 6 4 8 
4 1 3 0 0 0 0 0 0 
0 0 7 0 0 2 0 9 0 
2 0 1 0 6 0 8 0 4 
0 8 0 5 0 4 0 1 2
 

2829

0 0 0 7 0 2 4 5 3 
9 0 0 0 0 8 0 0 0 
7 4 0 0 0 5 0 1 0 
1 9 5 0 8 0 0 0 0 
0 7 0 0 0 0 0 2 5 
0 3 0 5 7 9 1 0 8 
0 0 0 6 0 1 0 0 0 
0 6 0 9 0 0 0 0 1 
0 0 0 0 0 0 0 0 6

2852

說明

【數據範圍】

40%的數據，數獨中非 0 數的個數不少於 30。

80%的數據，數獨中非 0 數的個數不少於 26。

100%的數據，數獨中非 0 數的個數不少於 24。

NOIP 2009 提高組 第四題

　　分析：首先膜一下five20巨佬Orz%%%。數獨問題，那麽就搜索唄。但是直接暴搜肯定會炸掉，那麽就要考慮如何剪枝。首先很顯然每一行每一列還有每一個九宮格裏1-9的數字不能重復出現，那麽就放三個bool數組來判斷，然後還可以放一個bool數組來判斷某一個位置是否放了數。但是這些肯定還不夠。搜索的時候這樣定義

　　dfs(int rest,int sum)

　　其中rest表示當前還有多少個格子未填數字，sum表示當前得分總和。那麽每次先用一個三重循環來找當前狀態下，哪一個格子中可填的數最少，那就從這個格子開始填，這樣可以盡可能的減少搜索的分支。具體如何實現在代碼中解釋。（哦，對了，這題在洛谷上是開了O2才過的，應該還有更優的優化，但是這裏蒟蒻也想不到什麽更好的優化了，歡迎各位大佬來踩，指導一下蒟蒻）

　　Code：

 1 // luogu-judger-enable-o2
 2 //It is made by HolseLee on 21rd Apr 2018
 3 //Luogu.org P1074
 4 #include<cstdio>
 5 #include<cstring>
 6 #include<cstdlib>
 7 #include<cmath>
 8 #include<iostream>
 9 #include<iomanip>
10 #include<algorithm>
11 using namespace std;
12 const int N=10;
13 int ans=-1,a[N][N];
14 bool vis[N][N],vh[N][N],vl[N][N],vm[N][N];
15 int w[N][N]={
16   {0,0,0,0,0,0,0,0,0,0},
17   {0,6,6,6,6,6,6,6,6,6},
18   {0,6,7,7,7,7,7,7,7,6},
19   {0,6,7,8,8,8,8,8,7,6},
20   {0,6,7,8,9,9,9,8,7,6},
21   {0,6,7,8,9,10,9,8,7,6},
22   {0,6,7,8,9,9,9,8,7,6},
23   {0,6,7,8,8,8,8,8,7,6},
24   {0,6,7,7,7,7,7,7,7,6},
25   {0,6,6,6,6,6,6,6,6,6}};
26 inline int read()
27 {
28   char ch=getchar();int num=0;
29   while(ch<‘0‘||ch>‘9‘)
30     ch=getchar();
31   while(ch>=‘0‘&&ch<=‘9‘){
32     num=num*10+ch-‘0‘;
33     ch=getchar();}
34   return num;
35 }
36 inline int getm(int x,int y)
37 {
38   if(x<=3){
39     if(y<=3)return 1;
40     if(y<=6)return 2;
41     return 3;}
42   else if(x<=6){
43     if(y<=3)return 4;
44     if(y<=6)return 5;
45     return 6;}
46   else{
47     if(y<=3)return 7;
48     if(y<=6)return 8;
49     return 9;}
50 }
51 inline void dfs(int rest,int sum)
52 {
53   if(rest==0){
54     ans=max(ans,sum);return;}
55   int maxn=1e9+7,opt,x,y;
56   for(int i=1;i<=9;i++)
57     for(int j=1;j<=9;j++)
58       if(!vis[i][j]){
59       opt=0;
60       for(int k=1;k<=9;k++)
61     if(!vh[i][k]&&!vl[j][k]&&!vm[getm(i,j)][k])opt++;
62       if(opt<maxn)maxn=opt,x=i,y=j;}
63   opt=getm(x,y);
64   for(int i=1;i<=9;i++)
65     if(!vh[x][i]&&!vl[y][i]&&!vm[opt][i]){
66       vh[x][i]=vl[y][i]=vm[opt][i]=vis[x][y]=true;
67       dfs(rest-1,sum+w[x][y]*i);
68       vh[x][i]=vl[y][i]=vm[opt][i]=vis[x][y]=false;
69   }
70 }
71 int main()
72 {
73   int cnt=0,tot=0;
74   for(int i=1;i<=9;i++)
75     for(int j=1;j<=9;j++){
76       a[i][j]=read();
77       if(a[i][j]>0){
78     cnt++;
79     vis[i][j]=true;
80     vh[i][a[i][j]]=true;
81     vl[j][a[i][j]]=true;
82     vm[getm(i,j)][a[i][j]]=true;
83     tot+=(w[i][j]*a[i][j]);
84       }}
85   dfs(81-cnt,tot);
86   printf("%d",ans);
87   return 0;
88 }

洛谷P1074 靶形數獨 [搜索]