HDU 1950(LIS)
阿新 • • 發佈:2018-05-26
BE AI clu surf pic ecif pin targe cep
expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without rossing each other, is imminent. Bearing in mind that there may be housands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?
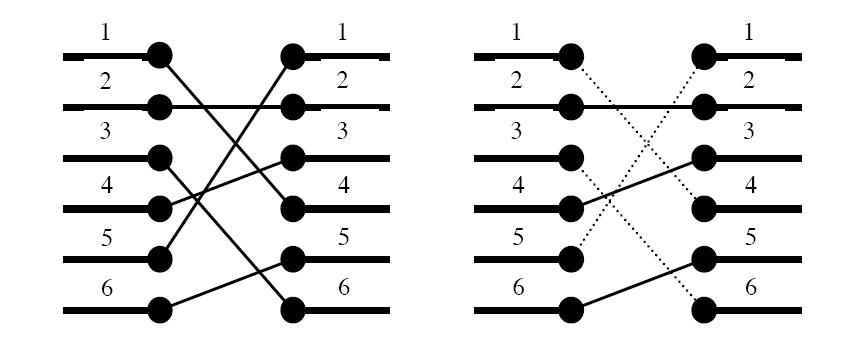
Figure 1. To the left: The two blocks‘ ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number pecifies which port on the right side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.
題目鏈接:
http://acm.hdu.edu.cn/showproblem.php?pid=1950
Bridging signals
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3711 Accepted Submission(s): 2337
expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without rossing each other, is imminent. Bearing in mind that there may be housands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?

Figure 1. To the left: The two blocks‘ ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number pecifies which port on the right side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.
Sample Input 4 6 4 2 6 3 1 5 1 0 2 3 4 5 6 7 8 9 1 0 1 8 8 7 6 5 4 3 2 1 9 5 8 9 2 3 1 7 4 6
Sample Output 3 9 1 4 分析: LIS問題,采用n*logn的算法優化一下
#include<bits/stdc++.h> #define max_v 100005 using namespace std; int a[max_v],dp[max_v],len; int select(int x) { int l,r,m; l=0; r=len; while(l<r) { m=l+(r-l)/2; if(dp[m]>=x) { r=m; }else { l=m+1; } } return l; } int main() { int t; scanf("%d",&t); while(t--) { int n; scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%d",&a[i]); } //dp[k]代表長度為k的LIS序列的最末元素,若有多個長度為k的上升子序列,則記錄最小的那個最末元素 //dp[]中的元素是單調遞增的,二分優化的時候利用這個性質 dp[1]=a[1]; len=1; for(int i=2; i<=n; i++) { if(a[i]>dp[len]) { dp[++len]=a[i]; } else { int j=select(a[i]); dp[j]=a[i]; } } printf("%d\n",len); } return 0; }
HDU 1950(LIS)
